08 Depth Estimation and 3D Reconstruction
Depth Estimation#
Introduction#
- 深度图表示为灰度,一般表示 \(1/z\),这样分布更均匀
- depth sensing
- active depth sensing: 激光雷达等
- passive depth sensing
- stereo
- monocular
- active stereo
- structured light
- TODAY: stereo vision,与 SfM 不同,需要稠密的深度计算
- find 2D-2D correspondences
- triangulate
Stereo Matching#
为什么 stereo matching 比光流简单?
- stereo 中两张图的视差是一定的,而光流可能有不同的运动方向
- 也即满足 \(\mathbf{u}_l^TF\mathbf{u}_r=0\)
- p.s. 这节课中默认使用齐次坐标
Recap: Epiploar Geometry#
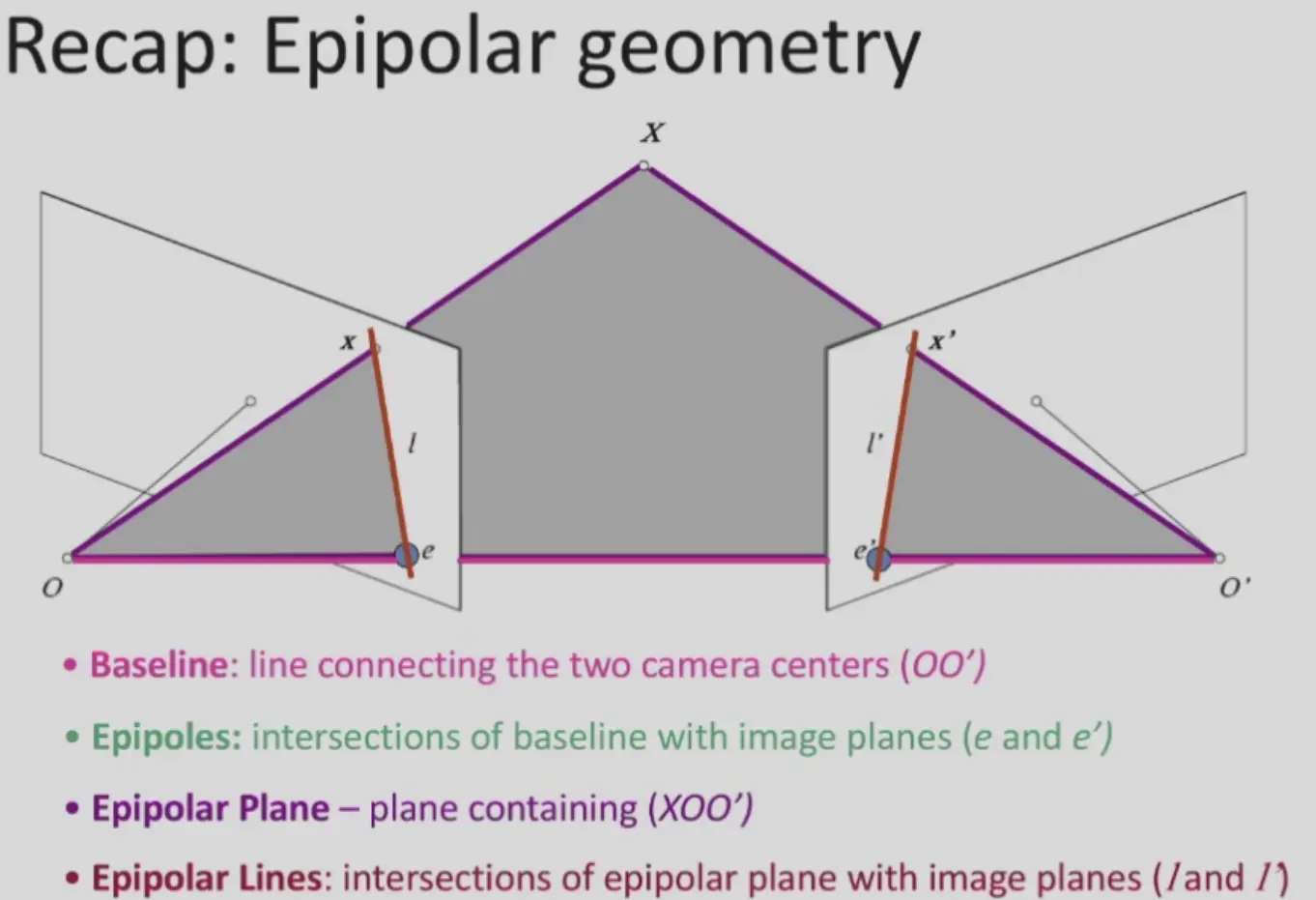
- baseline: 两个相机的连线
- epipole: baseline 和两个像平面的交点
- epipolar plane: baseline 和场景中一点构成的平面
- epipolar line: epipolar plane 和像平面的交线
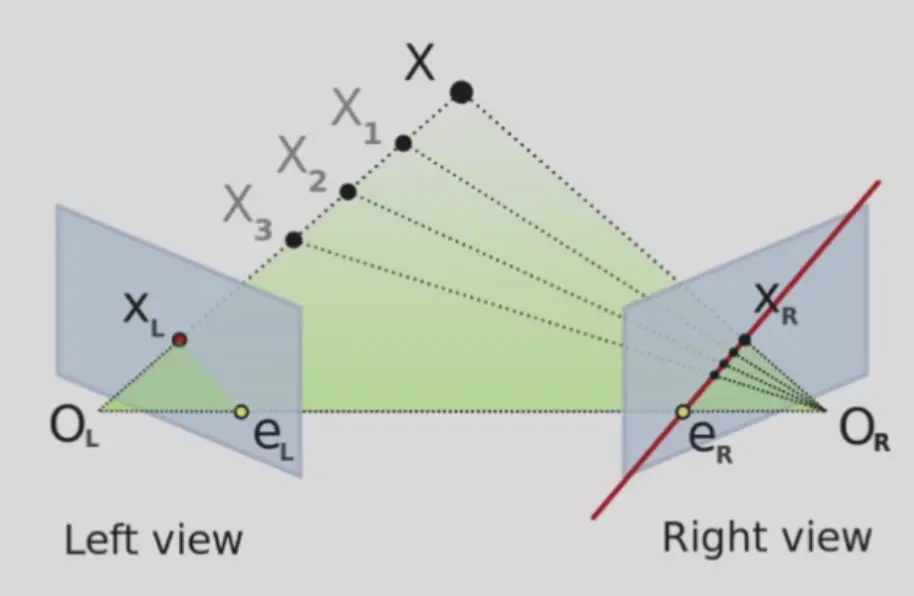
- 无论左边深度是多少,点在右侧的投影一定在 epipolar line 上
- 而且一定满足二维的 epipolar constraint
- 即 \(\mathbf{u}_l^TF\mathbf{u}_r=0\)
- 这实际上也是右侧 epipolar line 的解析式(将 \(\mathbf{u}_r\) 作为变量)

- 遍历左侧所有 pixel
- 对于每个 pixel,计算右侧的 epipolar line
- 在右侧 epipolar line 上找到最佳匹配点,triangulate 得到深度
simplest case: 当右侧的 epipolar line 水平
- 相机两个平面平行,且平行于 baseline
- 相机高度一样
- 相机的焦距一样
Disparity#
视差
Simplest Case#

在水平 epipolar line 的情况下:
\[
x_2-x_1=\text{the disparity of pixel }(x_1,y_1)
\]
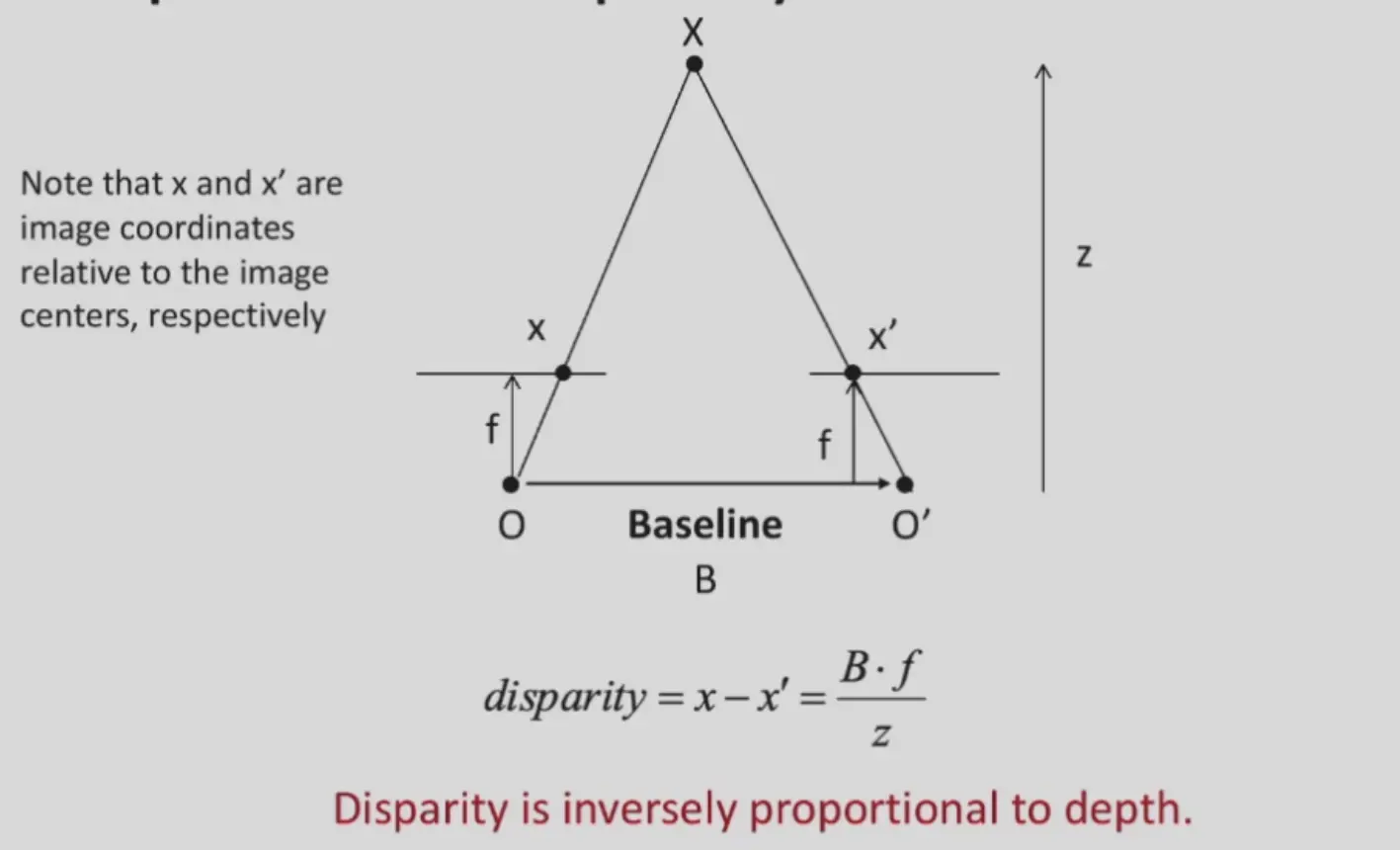
则有,这个条件下一致的深度为:
\[
\text{disparity}=\frac{Bf}{z}
\]
General Case#
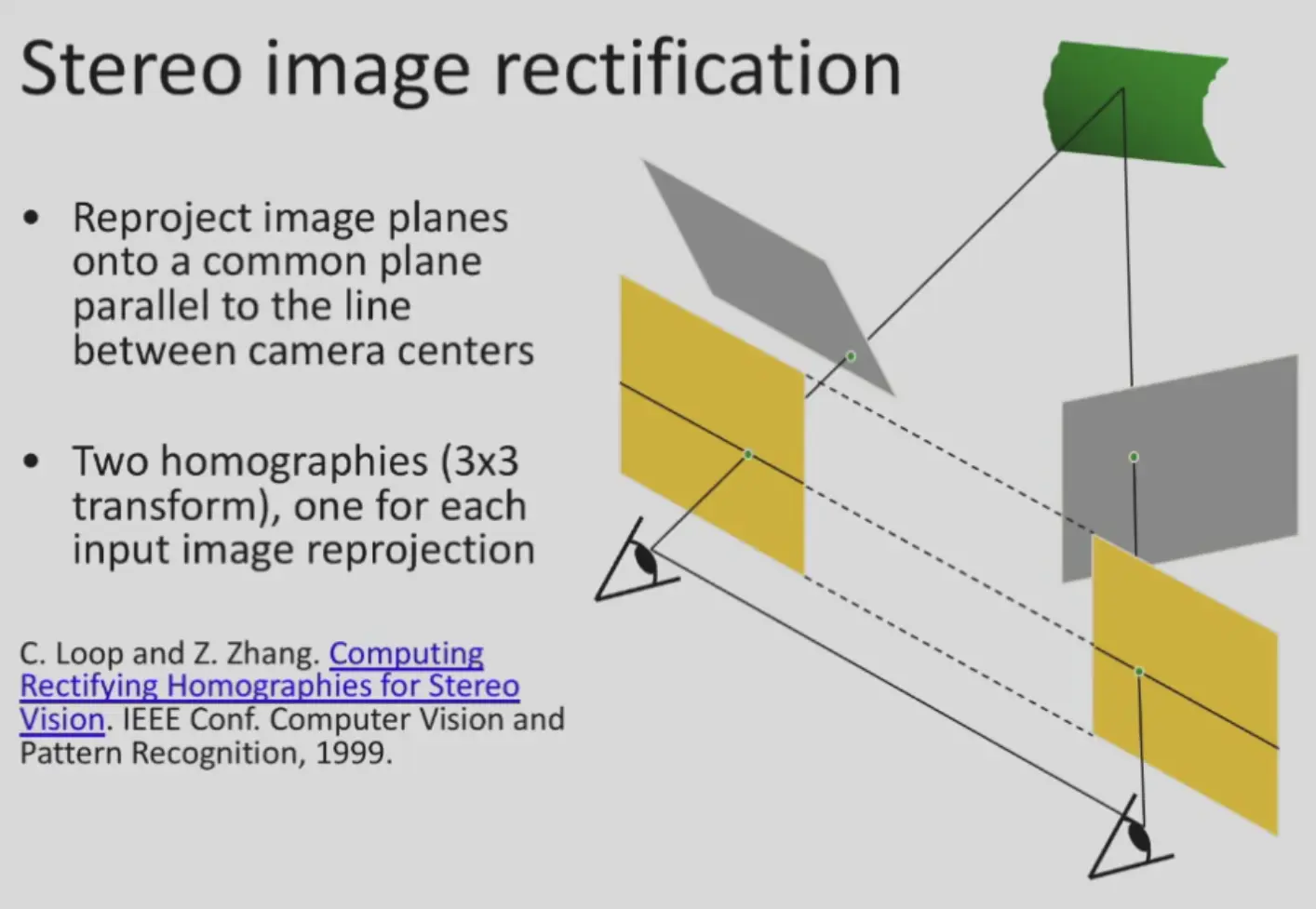
如果不满足上面的简单条件,可以使用两个 homographies 来 rectify
Matching Method#
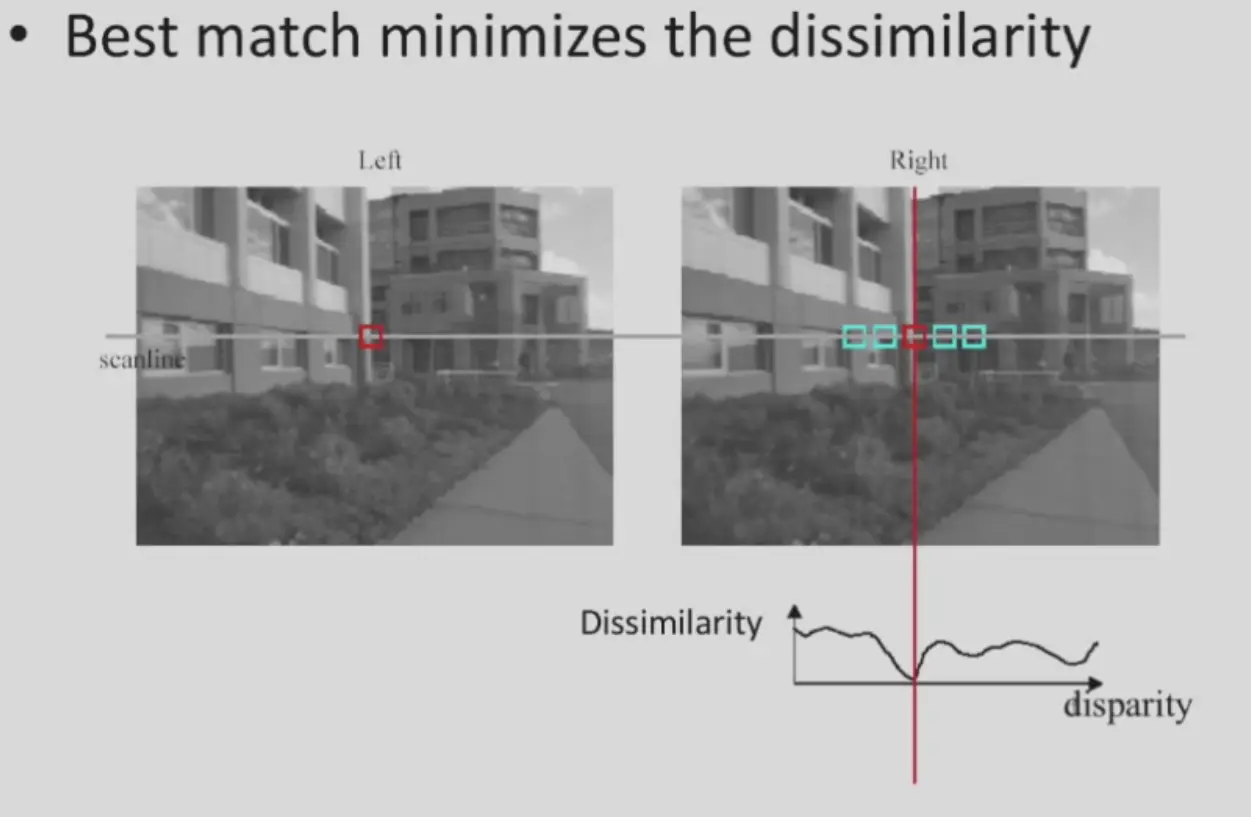
- 在每个像素周围取一个窗口,计算 score
- scores
- SSD(Sum of Squared Differences) \(\sum_{x,y} |W_1(x,y)-W_2(x,y)|^2\)
- SAD(Sum of Absolute Differences) \(\sum_{x,y} |W_1(x,y)-W_2(x,y)|\)
- ZNCC(Zero-mean Normalized Cross Correlation) \(\frac{\sum_{x,y}(W_1(x,y)-\bar{W}_1)(W_2(x,y)-\bar{W}_2)}{\sigma_{W_1}\sigma_{W_2}}\)
- 适用于不同相机、不同时刻拍摄,曝光参数乃至内参不同的情况

窗口太小会 noisy,窗口太大会 coarse
Add Smoothness#
What's the problem?#
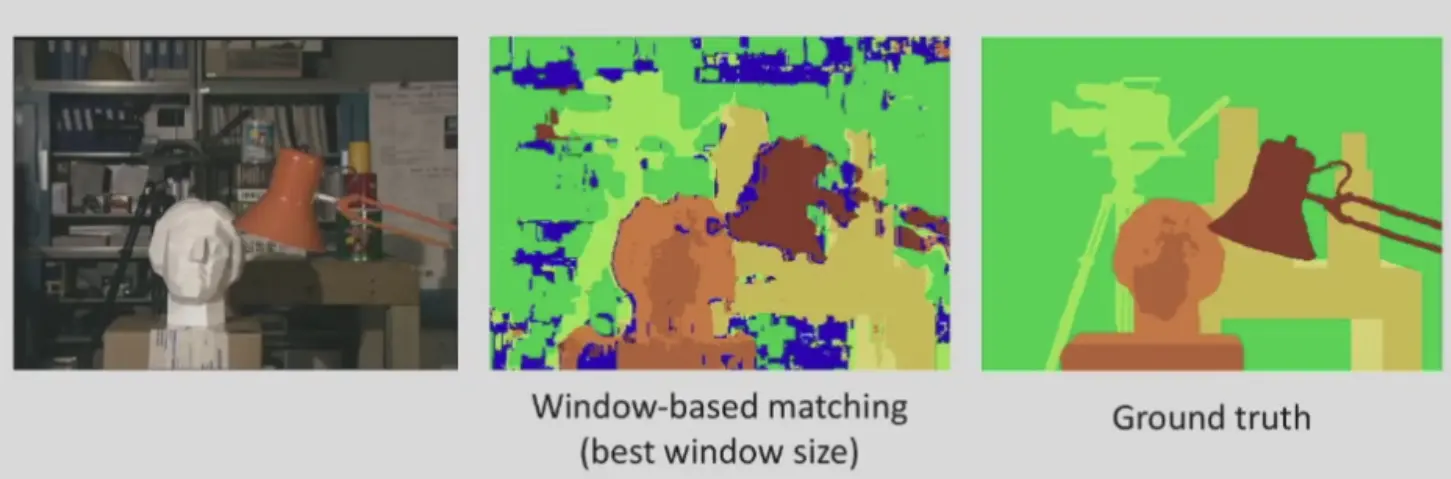
- 直接 window search 的缺点是噪声太多,但使用高斯滤波也会损失信息
- 考虑在匹配的时候就添加先验,即相邻的像素的深度相近
Markov Random Field#

- 引入马尔可夫随机场 \(E(d)\)
- 因为考虑了邻居的 smooothness,需要所有的 disparity 一起优化
- match cost: \(E_d(d)=\sum_{(x,y)\in I} C(x,y,d(x,y))\) e.g. SSD, SAD, ZNCC
- smoothness cost: \(E_s(d)=\sum_{(p,q)\in\varepsilon} V(d_p,d_q)\)
- \(\varepsilon\) 表示 neighbour
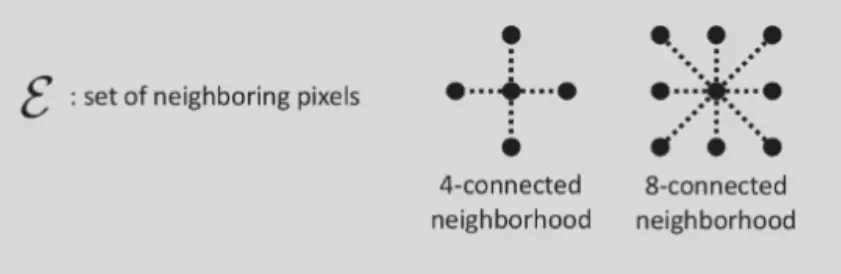
- \(V(d_p,d_q)\)
- L1 \(V(d_p,d_q)=|d_p-d_q|\)
- L0 \(V(d_p,d_q)=\begin{cases}0 &\text{ if }d_p=d_q\\1&\text{ if } d_p\neq d_q\end{cases}\)
- 不会过度平滑边缘
Solving#
- 可以在每条水平线上优化,可以用 dp 求解,但是纵向上无法比较连续
- 只能全局优化,需要更加复杂的算法
Summary: the Pipeline#
- calibrate cameras
- rectify images
- compute disparity
- estimate depth
baseline 大小的影响
- baseline 太小,导致视差小于单个像素,精度降低
- baseline 太大,会有遮挡,都看到的点比较小;而且匹配也更难
Question
- 相机标定误差
- 图像分辨率不够高
- 遮挡(occulations)
- 违反了亮度一致性(specular reflections 镜面反射)
- 透明
- 没有纹理
Active Stereo with Structured Light#
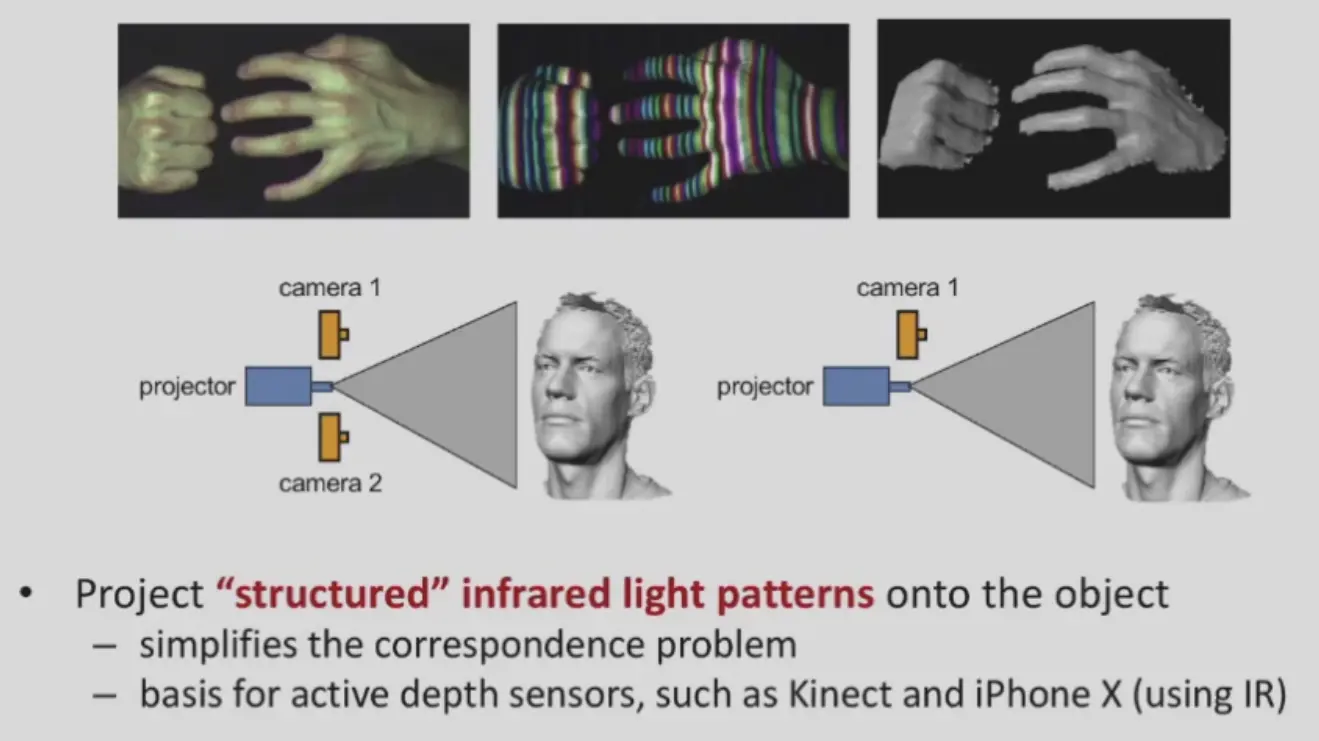
- 光是有结构的,能让 textureless 区域有了纹理,一般用红外光
- 只用一个红外相机,因为 projector 也有位姿信息
- 所以很多都是一个红外相机,一个 projector,一个 RGB 相机
Multi-view Stereo#
多目的立体匹配
- 优点
- 更强的约束
- 可以进行选择,例如选择一部分 best subset 去匹配其他图片
- 可以重建完整的 3D model,e.g. 360 degree
Basic Idea#

- 还是多个相机,找 epipolar line,选择合适的深度,使得其他相机看到的也正确
- 优化变量是点的深度,error 是到各个图像中的差别,e.g. SSD
Question
每个点都进行优化,计算量太大了,如何减少计算量?
Plane-Sweep#
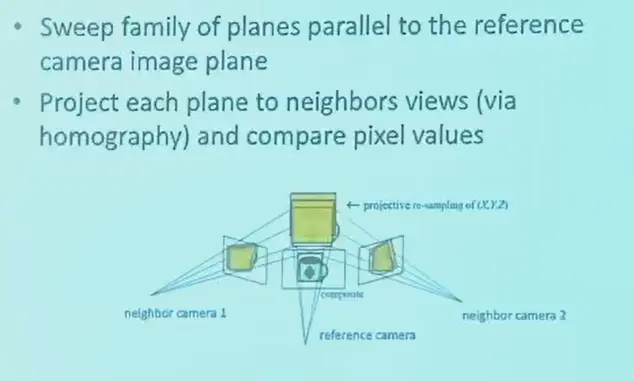
- sweep 是扫描的意思
- 有一系列的 sweep family plane,平行于 ref camera,深度不同
- 对于每一个 plane,假设深度就是这个 plane 的深度
- 然后投影到旁边的相机上,计算误差并保留,最终得到 cost volume
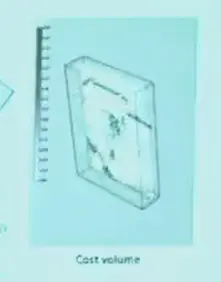
- 然后,对于每个像素,找到使得 cost 最小的深度即可
- 可以考虑加入 Markov Random Field 来获得比较光滑的深度图
Question
开销仍然比较大?是否有实时的算法?
Patch Match#
一种随机优化算法
Assumptions#
- 大量的像素,都进行随机深度猜测,总有可能正确的
- 相邻的像素深度相似
Method#
- init: 整张图随机初始化深度
- propagation: 将这个像素的深度赋予周边的像素,如果更好则保留
- local search: 对于每个像素,在深度邻域内进行 local search
- go to step 2
3D Reconstruction#
- 运行 SfM
- 使用 MVS 得到每张图的深度图
- 每个像素就是三维的点,多张图,能够得到比较稠密的三维模型
- 提取 mesh 并上色
3D Representations#
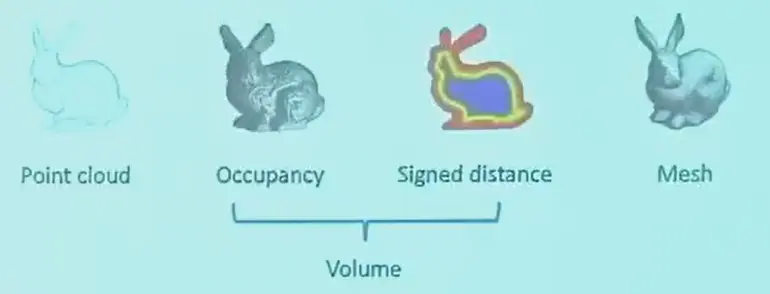
- point cloud
- volume
- occupancy: grid mesh,0/1 表示是否被占用
- signed distance: 距离物体表面的值,内部为负(SDF signed distance function)
- T(runcated)SDF
- mesh
3D Surface Reconstruction#
一般的做法
- point cloud to volume Poisson Reconstruction
- volume to mesh Marching Cubes
Poisson Reconstruction#
首先根据 MVS 得到密集点云。
然后计算每个点的法向,取周围点分布方差最小的方向,使用 PCA 计算。
假设 occupancy 函数为 \(\chi_M\),则其梯度在表面时,梯度就是 normal,将法向场表示为 \(\vec{V}\),因此优化目标为:
\[
\min_\chi ||\nabla\chi-\vec{V}||
\]
其解析解可以用 Poisson equation 解出。
Marching Cubes#
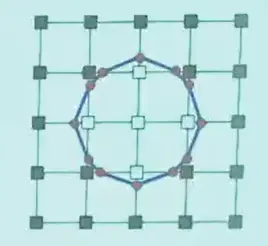
只考虑同时有黑白的格子,这说明存在边缘。
Occupancy 比较简单,直接设定格子内的面就行:
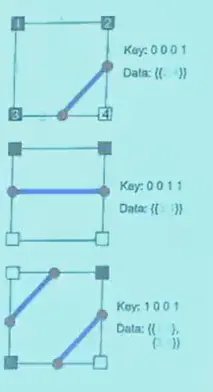
而 SDF 是连续的,更加精细,点的位置可以优化。
in 3D
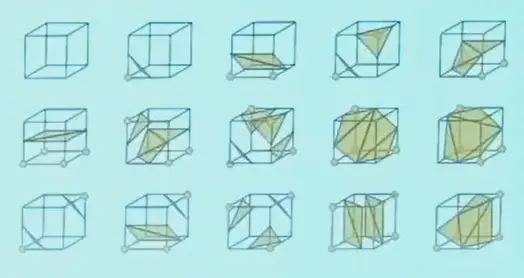
种类更多,一共 15 种。
Texture Mapping#
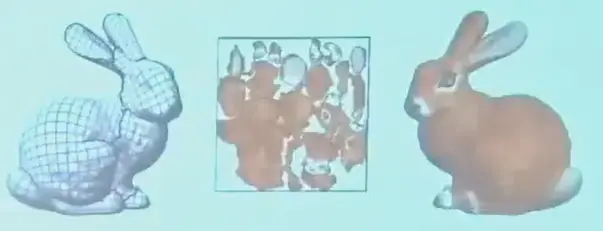
- mesh mapping: mesh 三个顶点与纹理图种的 u,v 坐标一一对应
- 插值,得到三角面片上的任意位置的对应坐标和对应颜色
- 将三维表面投影到二维纹理图,如何减少形变值得研究
Neural Scene Representations#
Question
volume 非常占空间,是否有更简单的表示方法?
- 一个网络可以描述任何函数,例如 SDF, color, occupancy,可以一起输出
- 更好优化,网格中的拓扑结构有很多离散约束,网络则是完全可微的
- 称为 NeRF 神经辐射场