05 Image Matching and Motion Estimation
Image Matching#
Feature 指的是图像中的点特征
Detection#
identify the interest points
- uniqueness: 找到和周围的点有最大区别的点,即角点
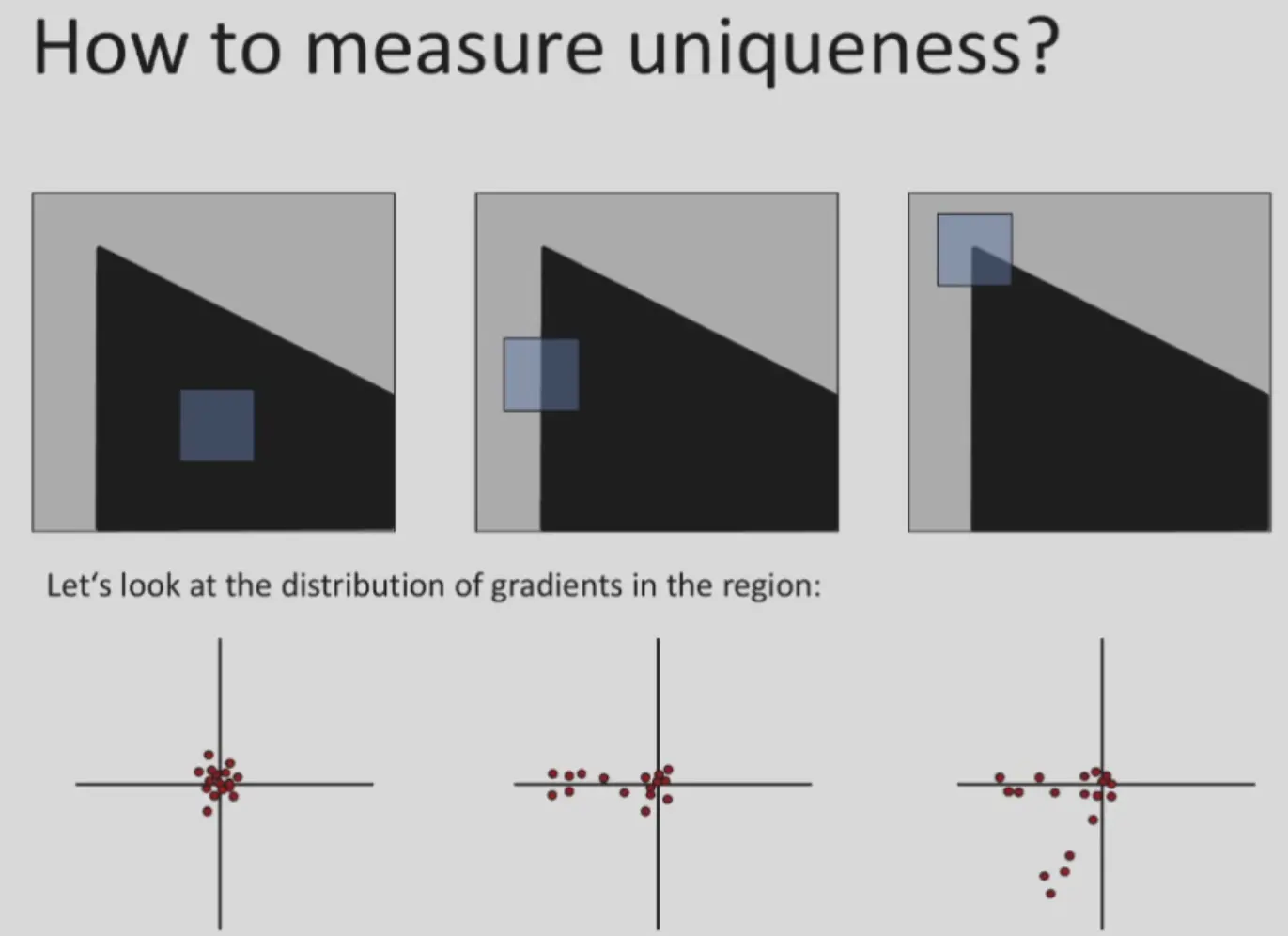
梯度的分布存在特征
进行 PCA,分析特征值,角点的两个特征值都应当比较大,对应两个方差最大的分布方向
Corner Detection#
- 构建协方差矩阵,因为要用到方差来衡量分布
\[
H=\sum_{\underbracket{(u,v)}_\text{window}} w(u,v)\begin{bmatrix}I_x^2 & I_x I_y \\ I_y I_x & I_y^2\end{bmatrix}\quad I_x=\frac{\partial I}{\partial x},I_y=\frac{\partial I}{\partial y}
\]
- 计算特征值
\[
H=\begin{bmatrix}a&b\\ c&d\end{bmatrix}\quad \lambda_{\pm}=\frac{1}{2}((a+d)\pm\sqrt{4bc+(a-d)^2})
\]
- 分类,\(\lambda_1,\lambda_2\) 都比较大的是 corner;Harris Operator 则简化为考虑
\[
f=\frac{\lambda_1\lambda_2}{\lambda_1+\lambda_2}=\frac{\det(H)}{\text{tr}(H)}
\]
- 由于 \(f\) 是连续的,找局部最大值。
Repeatability#
希望一张图中的特征点都能在另一张图中检测出来,所以需要保证一些不变性
- 亮度(曝光):梯度大小会发生变化,但是极值位置没有变化
- 平移:不变
- 旋转:协方差矩阵会变,但是特征值大小不变
-
缩放会变,因为窗口大小是固定的,角点是有尺度的
Scale Invariance#
- 选择不同的窗口大小。计算 \(f\) 值,找尺度上的极大值,这个极大值是不变的
- 实际上更多是变图像的大小,不断缩小,用同样的窗口进行处理
Blob Detection#
斑点检测
- 使用 Laplacian of Gaussian 滤波器,核心是任意方向的二阶导都很大
- 由于二阶导对噪声敏感,使用 gaussian 平滑,然后计算 laplacian
Laplacian of Gaussian#
\[
\nabla^2(I * g)=I*(\nabla^2g)
\]
其中 \(\nabla^2 g\) 是拉普拉斯高斯卷积核,这样可以减少卷积次数,加速计算/
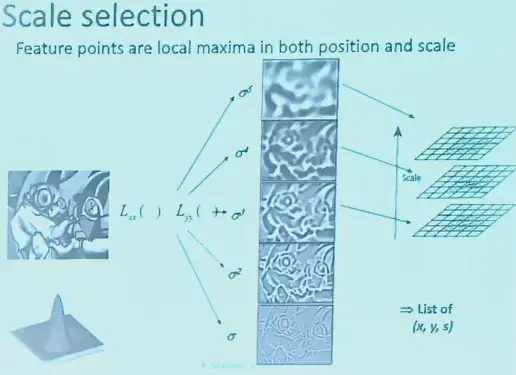
最后还是要在尺度和图像局部取极大值。
Difference of Gaussian#
可以将 LoG 近似为两个高斯卷积的差
\[
\nabla^2 G_\sigma\approx G_{\sigma_1}-G_{\sigma_2}
\]
结合图像金字塔,只用计算不同尺度的高斯卷积,然后两两相减就好
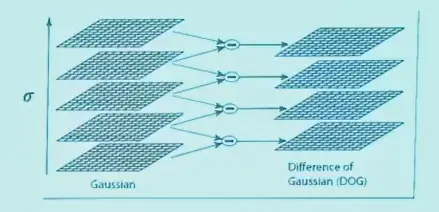
Summary#
- a good feature point
- unique
- invariant to transformations
- popular detectors
- Harris corner dector
- Blob detector (e.g. LoG, DoG)
Description#
extract vector feature
What is a good descriptor?#
- transformation/scale/photometric 不变性
SIFT Descriptor#
关注梯度方向的分布
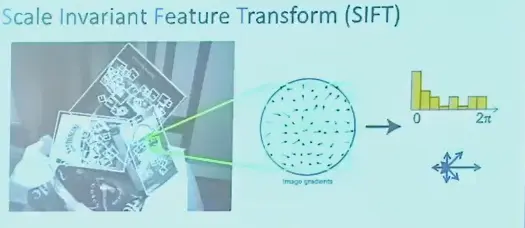
- 将梯度分布的直方图作为一个一维的特征
- 具有平移不变性
- 旋转后柱状图平移,但是可以通过归一化等操作对齐
- 亮度不变性,因为只考虑了梯度方向
- scale 不变性来自 harris 选择的窗口,已经找到了最合适的窗口,所以具有 scale 不变性
-
目前最常用的描述子
Lowe's SIFT Algorithm#
- DoG,在图像和 scale 上找局部最大值
- 找到主要朝向(dominate orientation)
- 创建直方图描述子
Matching#
- 如何匹配描述子?暴力算法,逐个匹配,找最近邻
- 使用 L2 norm 来计算描述子的距离
-
歧义性,例如重复的纹路、栏杆
- 方法一:raito test,最接近的距离/第二接近的距离,如果接近 1,说明有歧义性,则放弃这一对
- 方法二:保证相互都是最近邻
-
Learning Based Matching#
例如,白天黑夜的图像匹配、三维变化大的匹配
- 输入:原始图像
- 角点检测:输出一个热力图
- 描述子:输出卷积后每一个点的 latent feature
Motion Estimation#
Feature-tracking#
- 稀疏的,只计算一些特征点的运动轨迹
- 输出离散的点
Optical Flow#
- 在每一个像素位置都计算 image motion
- 输出稠密的运动场(optical flow)
-
不能仅靠特征匹配来完成
Lucas-Kanade#
Key Assumptions
- small motion: 点的运动距离不会特别远
- brightness constancy: 同一个点在不同帧中看起来是一样的
- spatial coherence: 点和它的邻居的移动相似
Brightness Constancy#
亮度不变方程:
\[
I(x,y,t)=I(x+u,y+v,t+1)
\]
近似,假设 \(u,v\) 很小,泰勒展开:
\[
I(x+u,y+v,t+1)\approx I(x,y,t)+I_xu+I_yv+I_t
\]
得到方程:
\[
I_xu+I_yv+I_t=0\quad\text{or}\quad\nabla I\cdot\begin{bmatrix}u & v\end{bmatrix}^T+I_t=0
\]
Spatial Coherence#
考虑邻近的 5x5 窗口,得到 25 个方程:
\[
\begin{bmatrix}
I_x(p_1) & I_y(p_1)\\
\vdots & \vdots\\
I_x(p_25) & I_y(p_25)
\end{bmatrix}
\begin{bmatrix}
u \\ v
\end{bmatrix}
=-
\begin{bmatrix}
I_t(p_1)\\ \vdots \\ I_t(p_25)
\end{bmatrix}
\]
此时可以用 \(A\cdot d=b\) 来表示这个线性方程组,求 \(\arg\min_x ||Ad-b||^2\),其解析解由 \((A^TA)d=A^Tb\) 给出,即:
\[
\begin{bmatrix}
\sum I_xI_x & \sum I_xI_y \\
\sum I_yI_x & \sum I_yI_y
\end{bmatrix}
\begin{bmatrix}
u \\ v
\end{bmatrix}
=-
\begin{bmatrix}
\sum I_xI_t \\ \sum I_yI_t
\end{bmatrix}
\]
Errors in Lukas-Kanade#
- 假设了协方差矩阵 \(A^TA\) 是简单可逆的
- 在光滑面或者边缘上,是算不出来运动的,关键是 \(A^TA\) 不可逆;纹理丰富的区域比较好做光流。
- 假设了噪声很小
- 亮度不一定完全一样
-
可以用梯度图
- 假设了运动很小,但很多情况下并不小
-
降采样后进行计算
-
coarse to fine
-
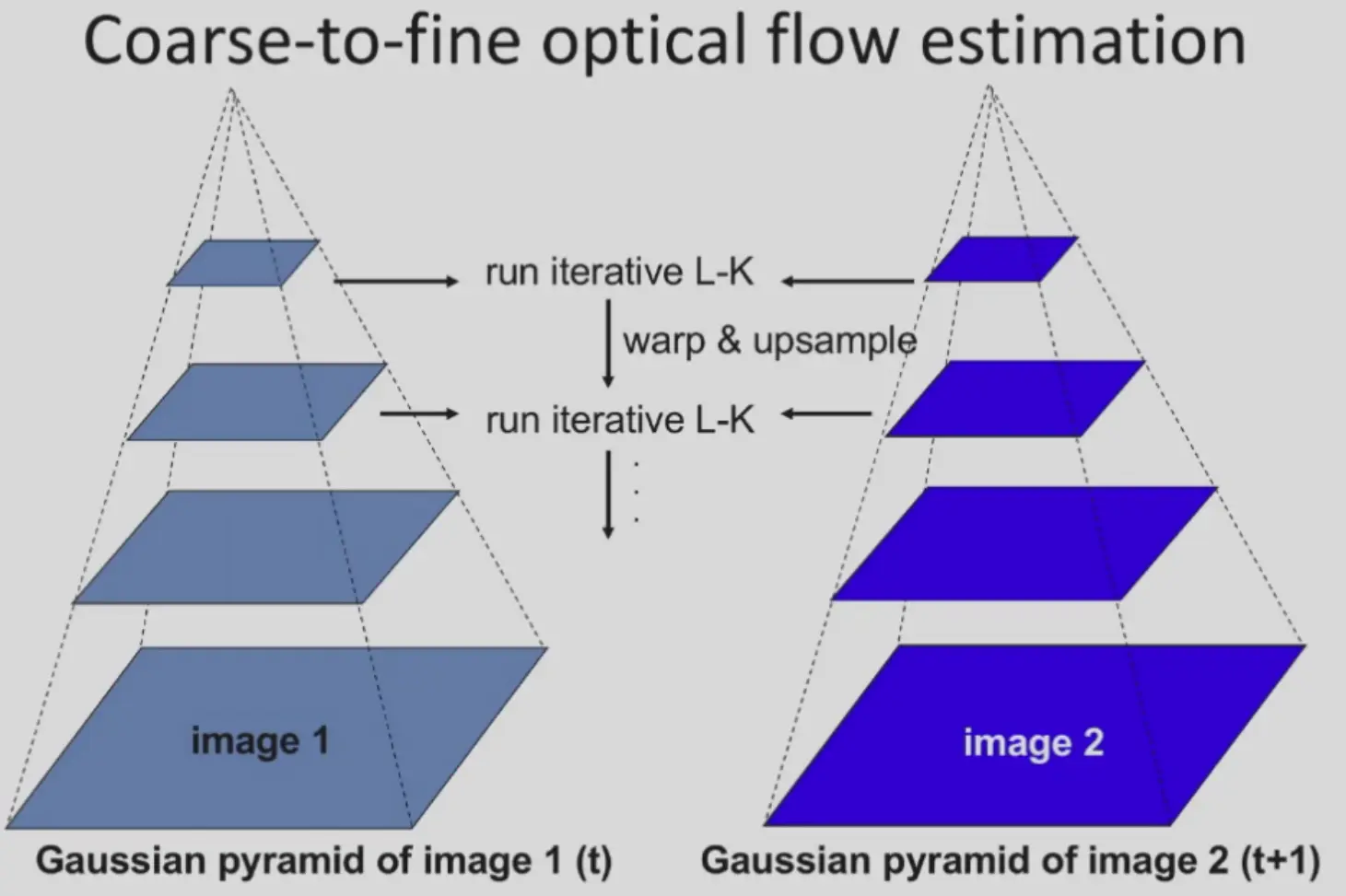
Coarse to fine
- 在最小的图片上算光流
- 在下一层,根据已有的计算结果先移动像素,再计算光流,相当得到了更加精细的光流效果
- 将所有光流结果叠加,再进入下一层计算

Application#
- 视频防抖
- 视频去噪,前后帧对应像素的平均
