06 Image Stiching
Image Warping#
- filtering: 只改变图像的像素值
- warping: 整体对图像进行变换
- global warping: 全局像素,使用同样的线性映射得到新像素 \(\mathbf{x}'=\mathbf{Mx}\),包括 homogenous 平移
Affine Transformation#
\[
\begin{pmatrix}x'\\y'\\1\end{pmatrix}\:=\:\begin{pmatrix}a&b&t_x\\c&d&t_y\\0&0&1\end{pmatrix}\cdot\begin{pmatrix}x\\y\\1\end{pmatrix}
\]
其中最后一行是 \(\begin{pmatrix}0&0&1\end{pmatrix}\),因此称为仿射变换
Projective Transformation#
投影变换(Homography),自由度更高
\[
\begin{aligned}
\begin{bmatrix}
x_i^{\prime} \\
y_i^{\prime} \\
1
\end{bmatrix}&\cong
\begin{bmatrix}
h_{00} & h_{01} & h_{02} \\
h_{10} & h_{11} & h_{12} \\
h_{20} & h_{21} & h_{22}
\end{bmatrix}
\begin{bmatrix}
x_i \\
y_i \\
1
\end{bmatrix} \\
x_{i}^{\prime}&=\frac{h_{00}x_{i}+h_{01}y_{i}+h_{02}}{h_{20}x_{i}+h_{21}y_{i}+h_{22}} \\
y_{i}^{\prime}&=\frac{h_{10}x_{i}+h_{11}y_{i}+h_{12}}{h_{20}x_{i}+h_{21}y_{i}+h_{22}}
\end{aligned}
\]
- 自由度问题
- 一共有 9 个参数,但是只有 8 个自由度,因为是在齐次坐标系下
- Homography matrix is up to scale,乘以一个 scaler 表示的还是同一个变换
- 通常添加限制,让向量 \([h_{00},h_{01},\dots,h_{22}]\) 的长度为 1
- 性质
- 变换矩阵一定可逆,即总是能找到一一对应的关系
- 换句话说,不能有一部分点出现和消失
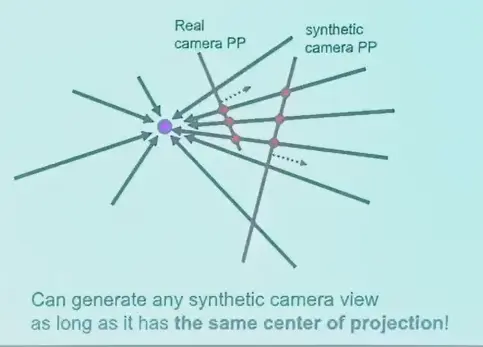
满足 Homography 的变换
- 相机位置不变,改变像平面(旋转和变焦),像素的变化符合单应变换
- 所有点都在同一个平面上,相机移动也可以
Summary of 2D Transformations#
| Transformations | Degree |
|---|---|
| translation | 2 |
| euclidean(translation + rotation) | 3 |
| similarity(euclidean + scale) | 4 |
| affine | 6 |
| projective | 8 |
Implementing Image Warping#
- 矩阵求逆,得到逆变换矩阵
- 对于新图像的每个格点,逆变换
- 双线性插值,得到需要的像素值(可能在原来图像外面)
Image Stiching#
- 特征匹配
- 根据匹配到的点对,求解变换
for Affine#
每一对特征匹配对应两个方程:
\[
\begin{bmatrix}
x'\\ y'\\ 1
\end{bmatrix}
=
\begin{bmatrix}
a&b&c\\ d&e&f\\ 0&0&1
\end{bmatrix}
\begin{bmatrix}
x\\ y\\ 1
\end{bmatrix}
=
\begin{bmatrix}
ax+by+c\\ dx+ey+f\\ 1
\end{bmatrix}
\]
也可以展开写成:
\[
\begin{bmatrix}x'\\ y'\end{bmatrix}
=
\begin{bmatrix}
x&y&1&0&0&0\\ 0&0&0&x&y&1
\end{bmatrix}
\begin{bmatrix}
a\\ b\\ c\\ d\\ e\\ f
\end{bmatrix}
\]
如果有 \(n\) 对特征点,那么得到 \(2n\) 个方程,记为 \(\mathbf{At}=\mathbf{b}\):
\[
\begin{bmatrix}
x_1 & y_1 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & x_1 & y_1 & 1 \\
x_2 & y_2 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & x_2 & y_2 & 1 \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
x_n & y_n & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & x_n & y_n & 1
\end{bmatrix}
\begin{bmatrix}
a \\
b \\
c \\
d \\
e \\
f
\end{bmatrix}=
\begin{bmatrix}
x_1^{\prime} \\
y_1^{\prime} \\
x_2^{\prime} \\
x_2^{\prime} \\
y_2^{\prime} \\
\vdots \\
x_n^{\prime} \\
y_n^{\prime}
\end{bmatrix}
\]
但实际上 \(n=3\) 就够了。
多数时候,特征匹配给的 \(n>>3\),改成优化问题,\(\text{minimize}||\mathbf{At}-\mathbf{b}||^2\),解析解为:
\[
\mathbf{t}=(\mathbf{A}^T\mathbf{A})^{-1}\mathbf{A}^T\mathbf{b}
\]
for Homographies#
\[
\begin{gathered}
\left.\left[
\begin{array}
{c}x_{i}^{\prime} \\
y_{i}^{\prime} \\
1
\end{array}\right.\right]\cong
\begin{bmatrix}
h_{00} & h_{01} & h_{02} \\
h_{10} & h_{11} & h_{12} \\
h_{20} & h_{21} & h_{22}
\end{bmatrix}
\begin{bmatrix}
x_{i} \\
y_{i} \\
1
\end{bmatrix} \\
x_{i}^{\prime}=\frac{h_{00}x_{i}+h_{01}y_{i}+h_{02}}{h_{20}x_{i}+h_{21}y_{i}+h_{22}} \\
y_{i}^{\prime}=\frac{h_{10}x_{i}+h_{11}y_{i}+h_{12}}{h_{20}x_{i}+h_{21}y_{i}+h_{22}} \\
x_{i}^{\prime}\left(h_{20}x_{i}+h_{21}y_{i}+h_{22}\right)=h_{00}x_{i}+h_{01}y_{i}+h_{02} \\
\begin{aligned}
y_{i}^{\prime}\left(h_{20}x_{i}+h_{21}y_{i}+h_{22}\right)=h_{10}x_{i}+h_{11}y_{i}+h_{12}
\end{aligned}
\end{gathered}
\]
实际上关于未知数,还是线性的。
一对匹配仍然两个方程:
\[
\left.\left[
\begin{array}
{ccccccc}x_i & y_i & 1 & 0 & 0 & 0 & -x_i^{\prime}x_i & -x_i^{\prime}y_i & -x_i^{\prime} \\
0 & 0 & 0 & x_i & y_i & 1 & -y_i^{\prime}x_i & -y_i^{\prime}y_i & -y_i^{\prime}
\end{array}\right.\right]
\begin{bmatrix}
h_{00} \\
h_{01} \\
h_{02} \\
h_{10} \\
h_{11} \\
h_{12} \\
h_{20} \\
h_{21} \\
h_{22}
\end{bmatrix}=
\begin{bmatrix}
0 \\
0
\end{bmatrix}
\]
\(n\) 对匹配得到方程组 \(\mathbf{Ah}=\mathbf{0}\),至少需要 4 对点,8 个方程:
\[
\begin{bmatrix}
x_1 & y_1 & 1 & 0 & 0 & 0 & -x_1^{\prime}x_1 & -x_1^{\prime}y_1 & -x_1^{\prime} \\
0 & 0 & 0 & x_1 & y_1 & 1 & -y_1^{\prime}x_1 & -y_1^{\prime}y_1 & -y_1^{\prime} \\
& & & & & \vdots \\
x_n & y_n & 1 & 0 & 0 & 0 & -x_n^{\prime}x_n & -x_n^{\prime}y_n & -x_n^{\prime} \\
0 & 0 & 0 & x_n & y_n & 1 & -y_n^{\prime}x_n & -y_n^{\prime}y_n & -y_n^{\prime}
\end{bmatrix}
\begin{bmatrix}
h_{00} \\
h_{01} \\
h_{02} \\
h_{10} \\
h_{11} \\
h_{12} \\
h_{20} \\
h_{21} \\
h_{22}
\end{bmatrix}=
\begin{bmatrix}
0 \\
0 \\
\vdots \\
0 \\
0
\end{bmatrix}
\]
优化目标为 \(\text{minimize}||\mathbf{Ah}-\mathbf{0}||^2\),这时需要对 \(\mathbf{h}\) 有额外约束,否则 \(\mathbf{f}=\mathbf{0}\)。所以加一个 \(||\mathbf{h}||_2=1\)。解析解为:
\[
\hat{\mathbf{h}}=\text{eigenvector of }\mathbf{A}^T\mathbf{A}\text{ with smallest eigenvalue}
\]
Outliers#
解决 outlier 问题的几种方法
- RANSAC
- 使用 L1 loss
RANSAC key insight
inlier 都是比较一致的,而 outlier 各有各的不同
- 尽可能少随机地取点
- fit model
- 进行投票
- 重复 N 次,保留最好的 model
- 把对这个 model 投票的点取出,再进行最小二乘
Stiching#
- DFS 找最小损失接缝
- 平均化
- 过渡/渐变
Panoramas#
Question
越往两侧,图像的拉伸越严重,需要另外的变换
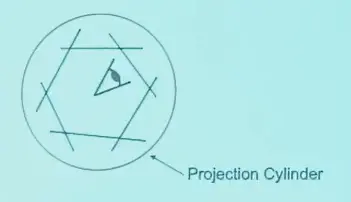
柱面投影

投影公式:
\[
\begin{aligned}
x'&=r\arctan(\frac{x}{f})\\
y'&=\frac{ry}{\sqrt{x^2+f^2}}
\end{aligned}
\]
注意,相机旋转在柱面上是平移,可以先投影到柱面上,然后计算平移来拼接,但是存在累积误差!
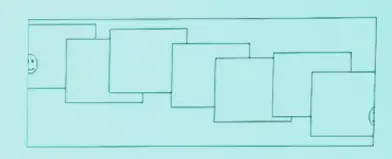
如果拍摄时精度足够,可以加一个纵向平移为 0 的约束