03 Image Processing
Image Processing Basics#
- contrast, blur, edge detection
Review: Convolution#
连续一维卷积
\[
(f * g)(x)=\int_{-\infty}^\infty f(y)g(x-y) \mathrm{d}y\\
\]
离散二维卷积
\[
\underbracket{(f*g)(x,y)}_\text{output image}=\sum_{i,j=-\infty}^\infty \underbracket{f(i,j)}_\text{filter} \cdot \underbracket{I(x-i,y-j)}_\text{input image}
\]
Padding#
- zero padding 一般够用
- edge values
- symmetric
Filter#
- box avg blur
- gaussian blur
- \(\sigma\) 越大,图像越模糊
- sharpen: \(I+(I-\text{blur}(I))\)
- bilateral filter
Image Sampling#
Aliasing#
- 信号变化太快,采样频率不够高,导致失真
Fourier Transform#
- 傅里叶变换:用一组正弦或余弦信号来逼近一个信号
- 傅里叶变换实际上计算的是频谱,也就是各个分量的权重
-
理解:求权重 ->求坐标 ->求内积
- \(e^{-i2\pi ux}\) 是频率为 \(u\) 的一个基,与 \(f(x)\) 乘求权重
- 还原原来的,用权重与基相乘
\[
\begin{aligned}
F(u)&=\int_{-\infty}^\infty f(x)e^{-i2\pi ux}\mathrm{d}x \\
f(x)&=\int_{-\infty}^\infty F(u)e^{-i2\pi ux}\mathrm{d}u
\end{aligned}
\]
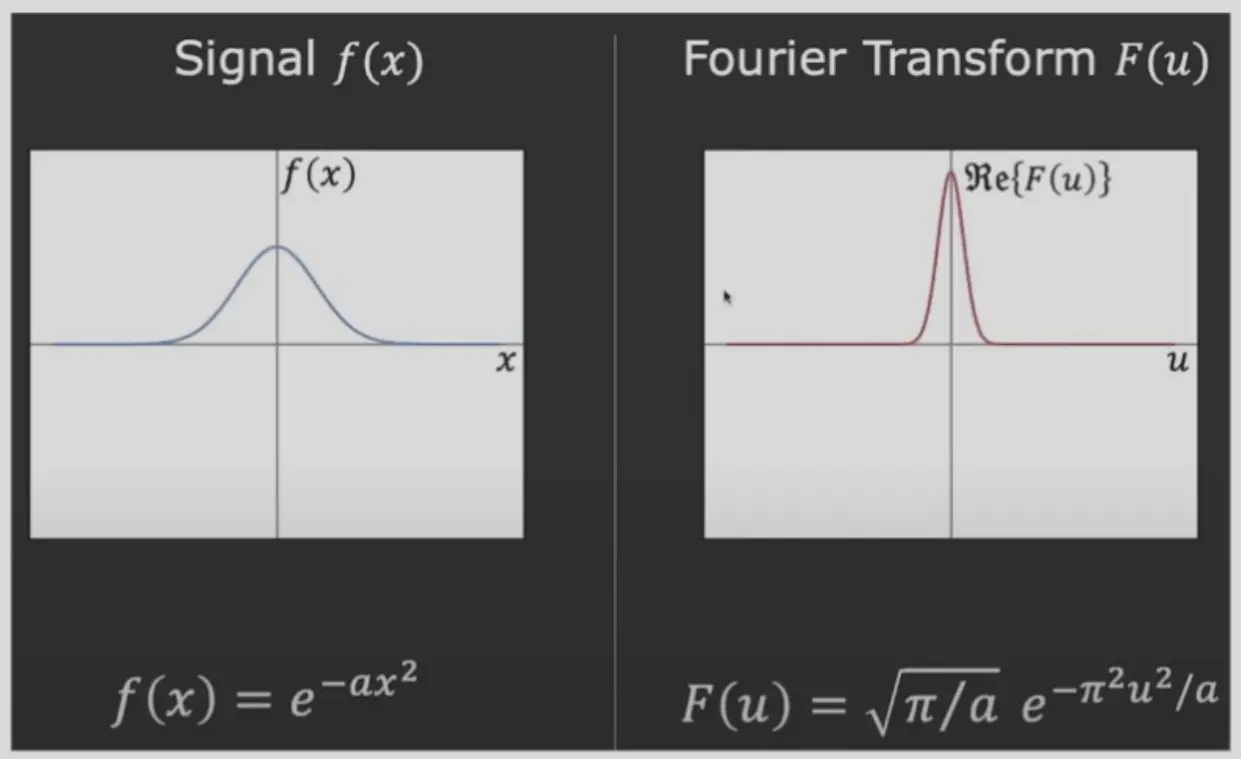
- 高斯函数的变换还是一个高斯函数,\(\sigma\) 互为倒数
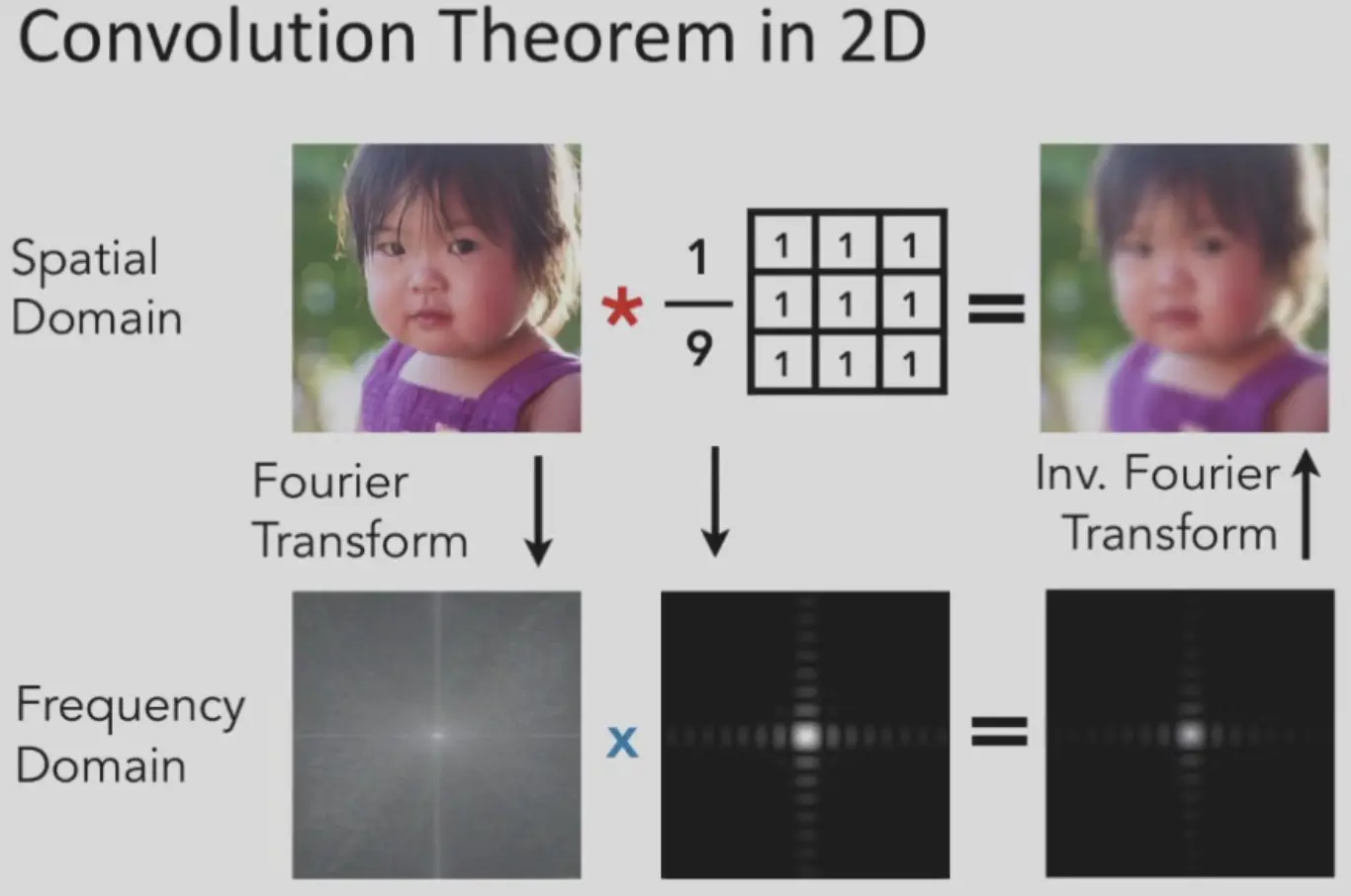
Convolution Theorem#

in 2D#

点 \((x,y)\) 的亮度表示了在 x 方向上频率为 \(x\),在 \(y\) 方向上频率为 \(y\) 的信号的强度
More about Aliasing#
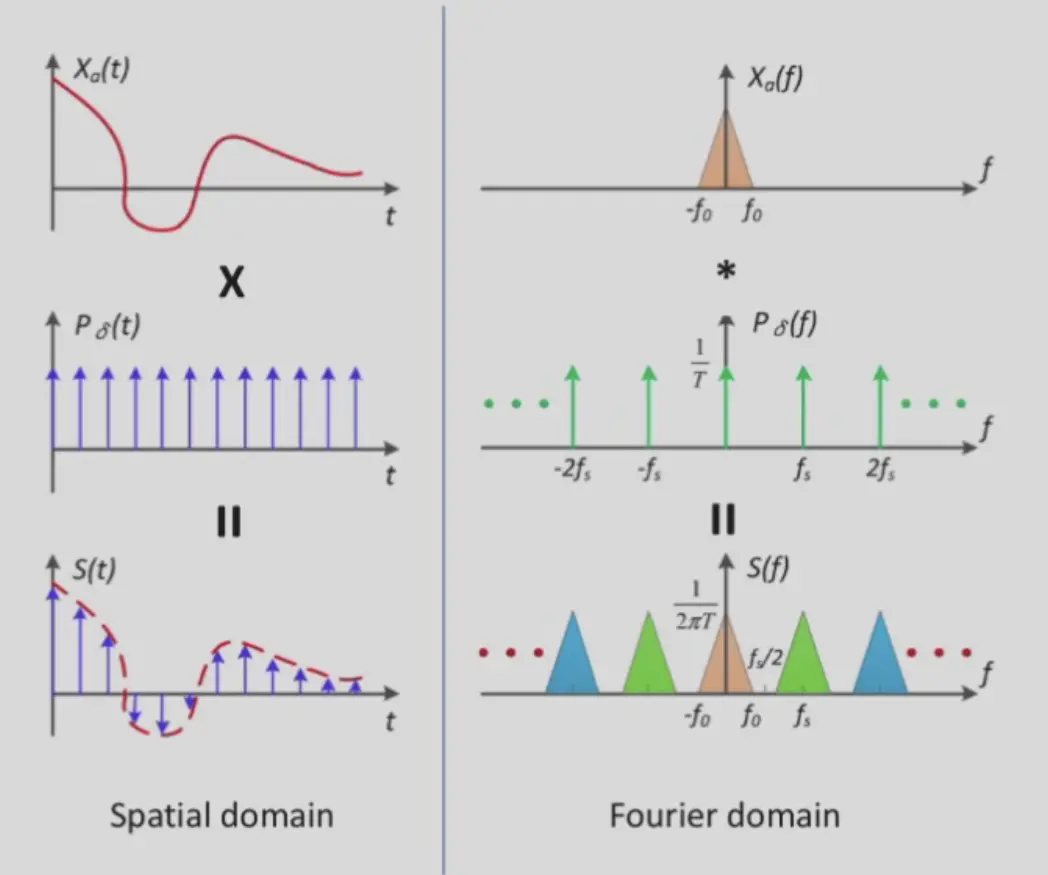
- 时域乘积(采样)对应频域卷积,但若发生混叠(三角形重合),就会导致无法还原原始信号
- 所以需要采样频率更高,使得右侧绿色频谱分布更稀疏
- 采样定理:一个频率为 \(f_0\) 的信号,采样频率至少为 \(2f_0\) 才能避免失真
-
为了避免缩小时的 aliasing,可以进行低通滤波,再降采样
Image Magnification#
Method#
- Interpolation
- Nearest-neighbor Interpolation
- Linear interpolation
- Cubic interpolation
- 如果希望补充更多信息,需要神经网络
Seam Carving#
Delete Pixels#
丢弃像素来实现图像变形。

像素重要性(Edge Energy)定义为 \(E(I)=|\frac{\partial I}{\partial x}|+|\frac{\partial I}{\partial x}|\),需要计算梯度,用卷积实现。

假设行删除一个像素,首先这些像素应当比较连续,其次重要性比较小,使用最短路径算法来实现。然后重复这个过程,达到删除若干像素的效果。
Add Pixels#
找到同样的路径,然后进行插值。