07 Structure from Motion
Introduction
SfM
根据一系列图像,重建相机的位姿和三维结构(稀疏点云),其中相机位姿更加重要
SfM extensions
- MVS 多视图立体集合
- visual localization 根据一张图求解相机位姿
- SLAM(simutaneous localization and mapping) 同时进行重建和定位
- SLAM 更注重同步、online、借助其他设备(如激光雷达),SfM 更注重 image、offline
Problems to be Noticed
- camera model:相机如何将三维点映射到平面
- camera calibration and pose estimation:如何计算世界坐标系下相机的位姿
- sfm: 如何重建三维场景
Camera Model
- coordinate transformation (extrinsic): 将世界模型转换到相机坐标系下
- Perceptive Projection (intrinsic): 相机成像投影
- image plane to image sensor mapping (intrinsic): 像平面转换为像素坐标
Extrinsic Parameters
对于同一点的在世界和相机下的坐标:
\[
\mathbf{x}_w=\begin{bmatrix}x_w\\ y_w\\ z_w\end{bmatrix}
\quad
\mathbf{x}_c=\begin{bmatrix}x_c\\ y_c\\ z_c\end{bmatrix}
\]
相机位姿参数有 \(\mathbf{c}_w\) 相机位置(3 个自由度)和旋转 \(R_{3\times3}\):
\[
R=
\begin{bmatrix}
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33}
\end{bmatrix}
\]
由此得到点转换到相机坐标系下的映射关系:
\[
\begin{aligned}
& \mathbf{x}_{c}=R(\mathbf{x}_{w}-\mathbf{c}_{w})=R\mathbf{x}_{w}-R\mathbf{c}_{w}=R\mathbf{x}_{w}+\mathbf{t}\quad\boxed{\mathbf{t}=-R\mathbf{c}_{w}} \\
& \mathbf{x}_{c}=
\begin{bmatrix}
x_{c} \\
y_{c} \\
z_{c}
\end{bmatrix}=
\begin{bmatrix}
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33}
\end{bmatrix}
\begin{bmatrix}
x_{w} \\
y_{w} \\
z_{w}
\end{bmatrix}+
\begin{bmatrix}
t_{x} \\
t_{y} \\
t_{z}
\end{bmatrix}
\end{aligned}
\]
in homogenous
可以表示为线性关系:
\[
\tilde{\mathbf{x}}_{c}=
\begin{bmatrix}
x_{c} \\
y_{c} \\
z_{c} \\
1
\end{bmatrix}=
\begin{bmatrix}
r_{11} & r_{12} & r_{13} & t_{x} \\
r_{21} & r_{22} & r_{23} & t_{y} \\
r_{31} & r_{32} & r_{33} & t_{z} \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x_{w} \\
y_{w} \\
z_{w} \\
1
\end{bmatrix}
\]
此时可以将外参记为一个外参矩阵 \(M_\text{ext}\):
\[
M_\text{ext}=
\begin{bmatrix}
R_{3\times3} & \mathbf{t} \\
\mathbf{0}_{1\times3} & 1
\end{bmatrix}=
\begin{bmatrix}
r_{11} & r_{12} & r_{13} & t_x \\
r_{21} & r_{22} & r_{23} & t_y \\
r_{31} & r_{32} & r_{33} & t_z \\
0 & 0 & 0 & 1
\end{bmatrix}
\]
Intrinsic Parameters
Perspective Projection
\[
\mathbf{x}_c=\begin{bmatrix}x_c\\ y_c\\ z_c\end{bmatrix}\Rightarrow
\mathbf{x}_i=f\cdot \begin{bmatrix}x_c/z_c\\ y_c/z_c\\ 1\end{bmatrix}
\]
Image Plane to Image Sensor Mapping
假设 xy 方向像素密度为 \(m_x,m_y\)(pixels/mm),则:
\[
u=m_xfx_i+c_x\quad v=m_yfy_i+c_y
\]
其中 \(c_x,c_y\) 是因为图像原点在左上角。
Intrinsic Matrix
\[
\begin{bmatrix}
u \\
v \\
1
\end{bmatrix}\cong
\begin{bmatrix}
f_x & 0 & c_x \\
0 & f_y & c_y \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x_c \\
y_c \\
z_c
\end{bmatrix}=
\begin{bmatrix}
f_x & 0 & c_x & 0 \\
0 & f_y & c_y & 0 \\
0 & 0 & 1 & 0
\end{bmatrix}
\begin{bmatrix}
x_c \\
y_c \\
z_c \\
1
\end{bmatrix} \quad
\boxed{
\begin{array}
{c}f_x=m_xf \\
f_y=m_yf
\end{array}}
\]
同样可以写成线性的关系 \(M_\text{int}\in \mathbb{R}^{3\times 4}\),描述了相机坐标下的点如何 map 到像素坐标,注意这里 \(f_x,f_y,c_x,c_y\) 的单位都是像素
Warning
如果图像经过了裁剪,\(c_x,c_y\) 可能不一样
Projection Matrix \(P\)
\[
\tilde{\mathbf{u}}=M_\text{int}M_\text{ext}\tilde{\mathbf{x}}_w
\]
完整的投影矩阵为:
\[
\begin{bmatrix}
\tilde{u} \\
\tilde{v} \\
\tilde{w}
\end{bmatrix}=
M_\text{int}M_\text{ext}
\begin{bmatrix}
x_w \\
y_w \\
z_w \\
1
\end{bmatrix}\quad \boxed{P=M_\text{int}M_\text{ext}={\begin{bmatrix}
p_{11} & p_{12} & p_{13} & p_{14} \\
p_{21} & p_{22} & p_{23} & p_{24} \\
p_{31} & p_{32} & p_{33} & p_{34}
\end{bmatrix}}=
\begin{bmatrix}
f_x & 0 & c_x & 0 \\
0 & f_y & c_y & 0 \\
0 & 0 & 1 & 0
\end{bmatrix}
\begin{bmatrix}
r_{11} & r_{12} & r_{13} & t_x \\
r_{21} & r_{22} & r_{23} & t_y \\
r_{31} & r_{32} & r_{33} & t_z \\
0 & 0 & 0 & 1
\end{bmatrix}
}
\]
Camera Calibration
标定,即求解相机的内外参
Camera Calibration Procedure
Solve \(P\)

标定板格点的世界坐标是已知的,世界坐标系同样也是由标定板确定的
由标定点,可以列出和 \(P\) 相关的线性表达:

用同样的方法,可以拆成 \(2n\) 个方程构成的方程组 \(A\mathbf{p}=\mathbf{0}\):

且由于齐次坐标的性质,\(kP\) 和 \(P\) 代表同样的变换,\(P\) is up to scale,可令 \(||\mathbf{p}||^2=1\),则求解问题为:
\[
\text{minimize }||A\mathbf{p}||^2\text{, such that }||\mathbf{p}||^2=1
\]
解析解是:
\[
\mathbf{p}=\text{eigenvector of }A^TA\text{ with the smallest eigenvalue}
\]
Decompose \(P\) to Intrinsic and Extrinsic Matrices
已经计算出 \(P\),回忆:
\[
P=M_\text{int}M_\text{ext}={\begin{bmatrix}
p_{11} & p_{12} & p_{13} & p_{14} \\
p_{21} & p_{22} & p_{23} & p_{24} \\
p_{31} & p_{32} & p_{33} & p_{34}
\end{bmatrix}}=
\begin{bmatrix}
f_x & 0 & c_x & 0 \\
0 & f_y & c_y & 0 \\
0 & 0 & 1 & 0
\end{bmatrix}
\begin{bmatrix}
r_{11} & r_{12} & r_{13} & t_x \\
r_{21} & r_{22} & r_{23} & t_y \\
r_{31} & r_{32} & r_{33} & t_z \\
0 & 0 & 0 & 1
\end{bmatrix}
\]
需要将 \(P\) 进行分解
Decompose 1
取 \(P[:,:3]\),即前三列,有:
\[
\begin{bmatrix}
p_{11} & p_{12} & p_{13} \\
p_{21} & p_{22} & p_{23} \\
p_{31} & p_{32} & p_{33}
\end{bmatrix}=
\begin{bmatrix}
f_x & 0 & o_x \\
0 & f_y & o_y \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{25} \\
r_{31} & r_{39} & r_{35}
\end{bmatrix}=KR
\]
然后进行 QR factorization,可以得到一个上三角矩阵乘以一个正交矩阵,就得到了 \(M_\text{int}\) 和旋转,下面只要求平移 \(t\)。
Decompose 2
又由于:
\[
\begin{bmatrix}
p_{14} \\
p_{24} \\
p_{34}
\end{bmatrix}=
\begin{bmatrix}
f_x & 0 & o_x \\
0 & f_y & o_y \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
t_x \\
t_y \\
t_z
\end{bmatrix}=K\mathbf{t}
\]
因此:
\[
\mathbf{t}=K^{-1}\begin{bmatrix}p_{14}\\ p_{24}\\ p_{34}\end{bmatrix}
\]
Summary
- 相机的内参基本是不会变的,外参则是一直变化的
- 有时相机内参也可以用 exif 信息得到
Perspective-n-Point Problem
Intro: Visual Localization Problem
- 三维点也有一个特征,在重建的时候生成
- 用二维图像的像素特征进行匹配,找到三维 - 二维关系
- 然后是一个 Perspective-n-Point(PnP),是一个已知内参求外参的问题
- 外参 6 个自由度,位置和旋转
- 理论上三对点就足够
- 先用标定的方法,得到 \(P\)
- 然后进行分解得到外参
- 这样,会需要 6 对点先求解 \(P\),误差更大,计算量更大
P3P
假设只有 3 对点,内参已知、世界坐标、图像坐标已知,求外参
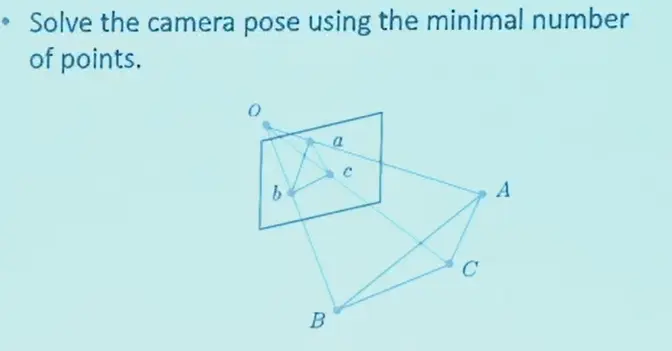
其本质上就是求解 \(OA,OB,OC\)。
使用余弦定理,进行化简得到:

这是一个二元二次方程,一般有 4 组解,需要额外的一对点来验证。
Optimization
minizing the reprojection error
\[
\min_{R,t}\sum_i ||p_i-K(RP_i+t)||^2
\]
这是一个非线性最小二乘优化问题,需要使用 LM 算法。
Note
- 初始猜测解可以使用 P3P 得到
- P3P 可能也会选到错误匹配,所以需要 RANSAC
Structure from Motion
没有标定板,只有一系列图像,内参矩阵已知,需要进行重建
procedure
- 假设相机的内参矩阵 \(K\) 已知,世界坐标以第一个相机为准
- 找到一些匹配点
- 计算第二个相机的相对 \(R\) 和 \(\mathbf{t}\)
- 计算点的三维位置
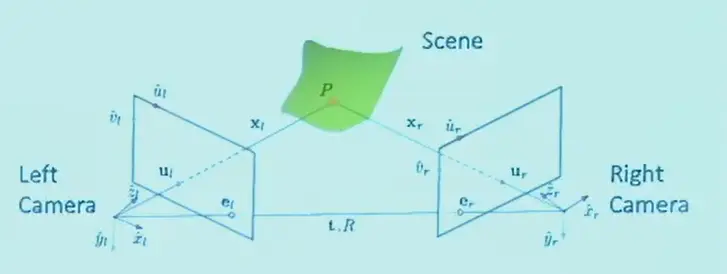
Epipolar Geometry
通过两个相机,计算其共同像素的三维像素坐标
- Epipole(极点): 第一个相机被第二个相机看到的位置
- \(e_l,e_r\) 是一对对极点,一对相机确定一组对极点
- Epipolar plane of Scene Point P:
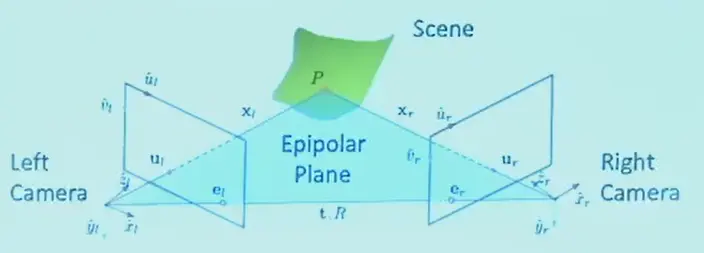
Epipolar Constraint
\(\mathbf{x}_l\) 与 \(\mathbf{x}_l\times\mathbf{t}\) 垂直,其中 \(\mathbf{x}_l\times\mathbf{t}\) 是 epipolar plane 的法向,展开得:
\[
\begin{aligned}
\mathbf{x}_l\cdot(\mathbf{x}_l\times\mathbf{t})=0\\\\
\Rightarrow \begin{bmatrix}x_l & y_l & z_l\end{bmatrix}\begin{bmatrix}t_yz_l-t_zy_l \\ t_zx_l-t_xz_l\\ t_xy_l-t_yx_l\end{bmatrix}=0\\\\
\Rightarrow \begin{bmatrix}x_l & y_l & z_l\end{bmatrix}\begin{bmatrix}0 & -t_z & t_y \\ t_z & 0 & -t_x \\ -t_y & t_x & 0\end{bmatrix}\begin{bmatrix} x_l \\ y_l \\ z_l\end{bmatrix}=0
\end{aligned}
\]
又有 \(\mathbf{x}_l=R\mathbf{x}_r+\mathbf{t}\),将右侧的 \(\mathbf{x}_l\) 替换,其中 \(\mathbf{t}\times\mathbf{t}=\mathbf{0}\) 得到:
\[
\begin{bmatrix}
x_l \\
y_l \\
z_l
\end{bmatrix}\left(
\underbrace{
\begin{bmatrix}
0 & -t_z & t_y \\
t_z & 0 & -t_z \\
-t_y & t_z & 0
\end{bmatrix}
\begin{bmatrix}
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33}
\end{bmatrix}
}_E
\begin{bmatrix}
x_r \\
y_r \\
z_r
\end{bmatrix}
+
\underbrace{
\begin{bmatrix}
0 & -t_z & t_y \\
t_z & 0 & -t_x \\
-t_y & t_z & 0
\end{bmatrix}
\begin{bmatrix}
t_x \\
t_y \\
t_z
\end{bmatrix}
}_{=0}
\right)=0
\]
所以:
Epipolar Constraint
\[
\begin{bmatrix}
x_l & y_l & z_l
\end{bmatrix}
\begin{bmatrix}
e_{11} & e_{12} & e_{13} \\
e_{21} & e_{22} & e_{23} \\
e_{31} & e_{32} & e_{33}
\end{bmatrix}
\begin{bmatrix}
x_r \\
y_r \\
z_r
\end{bmatrix}=0\quad\text{or}\quad
\mathbf{x}_l^TE\mathbf{x}=0
\]
得到 Essential Matrix \(E\):
\[
E=T_\times R
\]
\(E\) 只和两个相机本身的位置有关。
由于 \(T_\times\) 是一个 skew symmetric matrix(\(a_{ij}=-a_{ji}\)),\(R\) 是一个正交矩阵,可以用 SVD 奇异值分解 \(E\),得到这两个矩阵。
所以,只要有很多对 \(\mathbf{x}_l,\mathbf{x}_r\),就能列出 \(E\) 相关的方程,然后进行分解,得到 \(R\) 和 \(\mathbf{t}\),即相机之间的位置。
但是,点的三维坐标是未知的,所以研究一下二维坐标和三维坐标的关系。
对于左边的相机:
\[
z_l
\begin{bmatrix}
u_l \\
v_l \\
1
\end{bmatrix}=
\underbrace{
\begin{bmatrix}
f_x^{(l)} & 0 & o_x^{(l)} \\
0 & f_y^{(l)} & o_y^{(l)} \\
0 & 0 & 1
\end{bmatrix}
}_{K_1}
\begin{bmatrix}
x_l \\
y_l \\
z_l
\end{bmatrix}
\Rightarrow
\mathbf{x}_l^T=\begin{bmatrix} u_l & v_l & 1\end{bmatrix}z_l {K_l^{-1}}^T
\]
对于右边的相机:
\[
z_r
\begin{bmatrix}
u_r \\
v_r \\
1
\end{bmatrix}=
\underbrace{
\begin{bmatrix}
f_x^{(r)} & 0 & o_x^{(r)} \\
0 & f_y^{(r)} & o_y^{(r)} \\
0 & 0 & 1
\end{bmatrix}
}_{K_2}
\begin{bmatrix}
x_r \\
y_r \\
z_r
\end{bmatrix}
\Rightarrow
\mathbf{x}_r=K_r^{-1}z_r\begin{bmatrix}u_r\\ v_r\\ 1\end{bmatrix}
\]
代入 \(\mathbf{x}_l^TE\mathbf{x}=0\) 得到:
\[
\begin{bmatrix}
u_l & v_l & 1
\end{bmatrix}\cancel z_l
\underbrace{
K_l^{-1^T}
\begin{bmatrix}
e_{11} & e_{12} & e_{13} \\
e_{21} & e_{22} & e_{23} \\
e_{31} & e_{32} & e_{33}
\end{bmatrix}K_r^{-1}
}_F
\cancel z_r
\begin{bmatrix}
u_r \\
v_r \\
1
\end{bmatrix}=0
\]
这里的 \(K\) 是内参矩阵,是已知的,二维坐标也是已知的,所以未知数只有 \(E\)。记 \(F={K_l^{-1}}^TEK_r^{-1}\)。
Solving \(F\)
先求解:
\[
\begin{bmatrix}
u_l & v_l & 1
\end{bmatrix}F
\begin{bmatrix}
u_r \\
v_r \\
1
\end{bmatrix}=0
\quad\text{or}\quad
\left.\left[
\begin{array}
{ccc}u_l^{(i)} & v_l^{(i)} & 1
\end{array}\right.\right]
\begin{bmatrix}
f_{11} & f_{12} & f_{13} \\
f_{21} & f_{22} & f_{23} \\
f_{31} & f_{32} & f_{33}
\end{bmatrix}
\begin{bmatrix}
u_r^{(i)} \\
v_r^{(i)} \\
1
\end{bmatrix}=0
\]
这里的 \(F\) 也是 up to scale 的,所以设置约束 \(||F||_2=1\)。对每一对匹配点,都能得到一个关于 \(f\) 的线性方程:

至少需要 8 对点,优化目标为:
\[
\min_f||A\mathbf{f}||^2\text{ such that }||\mathbf{f}||^2=1
\]
然后可以得到 \(E\):
\[
E=K_l^TFK_r
\]
再使用奇异值分解 \(E=T_\times R\) 得到 \(\mathbf{t},R\)。
Triangulation
希望进一步得到三维点 \(P\) 的位置
左右两个相机坐标系下:
\[
\left.\left[
\begin{array}
{c}u_l \\
v_l \\
1
\end{array}\right.\right]\equiv
\begin{bmatrix}
f_y^{(l)} & 0 & o_x^{(l)} & 0 \\
0 & f_y^{(l)} & o_y^{(l)} & 0 \\
0 & 0 & 1 & 0
\end{bmatrix}\boxed{
\begin{bmatrix}
x_l \\
y_l \\
z_l \\
1
\end{bmatrix}}\quad
\begin{bmatrix}
u_r \\
v_r \\
1
\end{bmatrix}\equiv
\begin{bmatrix}
f_x^{(r)} & 0 & o_x^{(r)} & 0 \\
0 & f_y^{(r)} & o_y^{(r)} & 0 \\
0 & 0 & 1 & 0
\end{bmatrix}\boxed{
\begin{bmatrix}
x_r \\
y_r \\
z_r \\
1
\end{bmatrix}}
\]
其中,同一个点 \(P\) 的不同相机坐标系坐标来自外参的变换:
\[
\boxed{\begin{bmatrix}
x_l \\
y_l \\
z_l \\
1
\end{bmatrix}}=
\begin{bmatrix}
r_{11} & r_{12} & r_{13} & t_x \\
r_{21} & r_{22} & r_{23} & t_y \\
r_{31} & r_{32} & r_{33} & t_z \\
0 & 0 & 0 & 1
\end{bmatrix}\boxed{
\begin{bmatrix}
x_r \\
y_r \\
z_r \\
1
\end{bmatrix}}
\]
代入左侧相机的等式:
\[
\left.\left[
\begin{array}
{c}u_l \\
v_l \\
1
\end{array}\right.\right]\equiv
\begin{bmatrix}
f_x^{(l)} & 0 & o_x^{(l)} & 0 \\
0 & f_y^{(l)} & o_y^{(l)} & 0 \\
0 & 0 & 1 & 0
\end{bmatrix}
\begin{bmatrix}
r_{11} & r_{12} & r_{13} & l_x \\
r_{21} & r_{22} & r_{23} & l_y \\
r_{31} & r_{32} & r_{33} & l_z \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x_r \\
y_r \\
z_r \\
1
\end{bmatrix} \quad\text{or}\quad
\boxed{\tilde{\mathbf{u}}_l=P_l\tilde{\mathbf{x}}_r}
\]
再将右侧相机等式表示为:
\[
\boxed{\tilde{\mathbf{u}}_r=M_{\text{int}_r}\tilde{\mathbf{x}}_r}
\]
这两个等式中,只有 \(\tilde{\mathbf{x}}_r\) 是未知的,将两个方程联立写为:
\[
\left.\left[
\begin{array}
{ccc}u_rm_{31}-m_{11} & u_rm_{32}-m_{12} & u_rm_{33}-m_{13} \\
v_rm_{31}-m_{21} & v_rm_{32}-m_{22} & v_rm_{33}-m_{23} \\
u_lp_{31}-p_{11} & u_lp_{32}-p_{12} & u_lp_{33}-p_{13} \\
v_lp_{31}-p_{21} & v_lp_{32}-p_{22} & v_lp_{33}-p_{23}
\end{array}\right.\right]
\begin{bmatrix}
x_r \\
y_r \\
z_r
\end{bmatrix}=
\begin{bmatrix}
m_{14}-m_{34} \\
m_{24}-m_{34} \\
p_{14}-p_{34} \\
p_{24}-p_{34}
\end{bmatrix}
\quad\text{or}\quad
A_{4\times 3}\mathbf{x}_r=\mathbf{b}_{4\times 1}
\]
3 个未知数,4 个方程,是因为只有在完全没有误差的情况下,两条光线才会交于一点。改成优化问题,解析解为:
\[
\boxed{\mathbf{x}_r=\left(A^TA\right)^{-1}A^T\mathbf{b}}
\]
or by Optimization
minimize reprojection error
\[
\text{cost}(\mathbf{p})=||\mathbf{u}_l-\widehat{\boldsymbol{u}}_l||^2+||\mathbf{u}_r-\widehat{\boldsymbol{u}}_r||^2
\]
Multi-frame SfM
给定多张图像,如何进行上述步骤?
Sequential + Bundle Adjustment
- 先对前两张图进行求解,重建一个点云
- 计算第三张图
- 和点云特征进行匹配
- 解 PnP 问题得到第三张图的外参
- 将第三个相机新看到的点,进行三角化,让点云更多
- refine: bundle adjustment
\[
E\left(P_{proj},\mathbf{P}\right)=\sum_{i=1}^{m}\sum_{j=1}^{n}||u_{j}^{(i)}-P_{proj}^{(i)}\mathbf{P}_{j}||^{2}
\]
COLMAP
A general-purpose SfM and MVS pipeline with a graphical and command-line interface.







