04 Model Fitting and Optimization
Optimization#
\[
\begin{aligned}
\text{minimize } &f_0(x)\\
\text{subject to } &f_i(x)\leq 0, i=1,\dots,m\\
&g_i(x)=0,i=1,\dots,p
\end{aligned}
\]
Model Fitting#
\[
b=f(x;a)
\]
其中 \(x\) 是模型的参数
MSE#
fitting->optimization
\[
\hat{x}=\arg\min_x\sum_i(b_i-f(x;a_i))^2
\]
统计上的解释
假设数据具有高斯噪声,则极大似然估计 MLE 就是 MSE 函数的结果。
- 比较简单的线性模型,存在解析解
- 复杂的模型需要用梯度下降得到近似解
Taylor Expansion#
泰勒展开,二阶近似:
\[
F(x_k+\Delta x)\approx F(x_k)+J_F\Delta x+\frac{1}{2}\Delta x^TH_F\Delta x
\]
其中,Jacob Matrix (first-order derivative) 和 Hessian Matrix (second-order derivative) 分别为:
\[
\begin{aligned}
J_F&=\begin{bmatrix}\frac{\partial F}{\partial x_1} & \dots & \frac{\partial F}{\partial x_n}\end{bmatrix}\\
H_F&=\begin{bmatrix}
\frac{\partial^2 F}{\partial x_1^2} & \frac{\partial^2 F}{\partial x_1 \partial x_2} & \dots & \frac{\partial^2 F}{\partial x_1 \partial x_n} \\
\frac{\partial^2 F}{\partial x_2\partial x_1} & \frac{\partial^2 F}{\partial x_2^2} & \dots & \frac{\partial^2 F}{\partial x_2 \partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial^2 F}{\partial x_n \partial x_1} & \frac{\partial^2 F}{\partial x_n \partial x_2} & \dots & \frac{\partial^2 F}{\partial x_n^2}
\end{bmatrix}
\end{aligned}
\]
Gradient Descent#
找到使得 \(J_F \Delta x\) 最小的方向,可以直接令 \(\Delta x\) 的方向和 \(-J_F^T\) 相同,这样是最快梯度下降(Steepest GD)
如何找到合适的步长 \(\alpha\)?
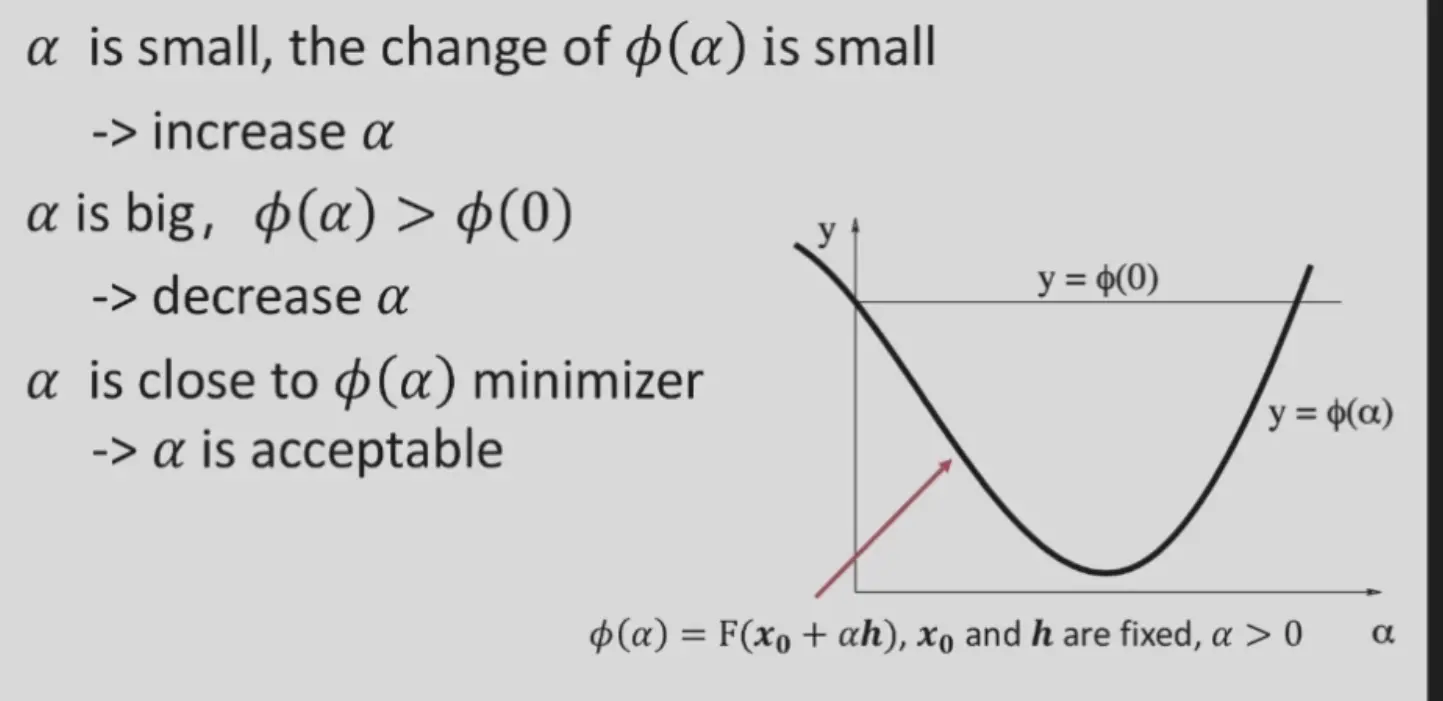
Backtracking Algorithm#
- 初始化一个比较大的 \(\alpha\)
- 不断减小 \(\alpha\),直到 \(\phi(\alpha)\leq\phi(0)+\gamma\phi'(0)\alpha\),其中 \(\gamma\in(0,1)\),能够确保不会差于更新前
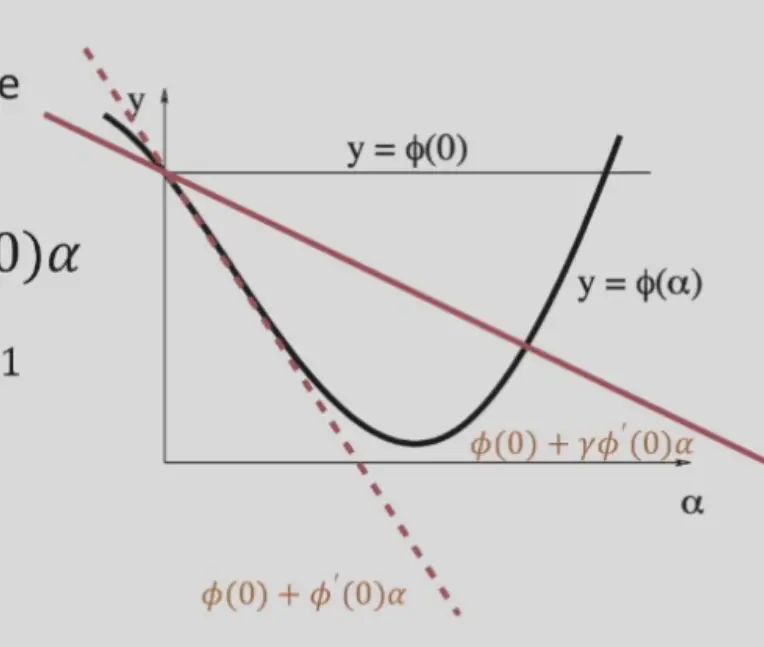
- 大部分情况下很好用,但是接近收敛时很慢
Newton Method#
\[
F(x_k+\Delta x)\approx F(x_k)+J_F\Delta x+\frac{1}{2}\Delta x^TH_F\Delta x
\]
要使右侧最小,求导:
\[
H_F\Delta x + J_F^T=0
\]
则更新为:
\[
\Delta x=-H_F^{-1}J_F^T
\]
- 收敛快
- 但是 Hessian 矩阵太大,需要很多计算资源,只能用于参数少的优化问题
Gauss-Newton Method#
用于解决非线性最小二乘问题
\[
\hat{x}=\arg\min_x F(x)=\arg\min_x ||R(x)||_2^2
\]
其中 \(R(x)=\begin{bmatrix}b_1-f(x;a_1) \\ b_2-f(x;a_2) \\ \vdots \\ b_n-f(x;a_n)\end{bmatrix}\) 为残差向量。
不直接展开 \(F\),而是展开 \(R\):
\[
\begin{aligned}
||R(x_k+\Delta x)||_2^2&\approx||R(x_k)+J_R \Delta x||_2^2\\
&=||R(x_k)||_2^2+2R(x_k)^TJ_R\Delta x+\Delta x^TJ_R^TJ_R\Delta x
\end{aligned}
\]
右侧求导等于 0:
\[
J_R^TR(x_k)+J_R^TJ_R\Delta x=0
\]
所以更新为:
\[
\Delta x=-(J_R^TJ_R)^{-1}J_R^TR(x_k)
\]
相比之下,Newton Method 的更新为 \(\Delta x=-H_F^{-1}J_F^T=-H_F^{-1}J_R^TR(x_k)\),所以 Gauss-Newton 使用 \(J_R^TJ_R\) 来近似 Hessian 矩阵
- 计算更快,收敛也比最速梯度下降快
- 但是 \(J_R^TJ_R\) 可能不可逆,eigen value = 0
Levenberg-Marquardt#
\[
\Delta x=-(J_R^TJ_R+\lambda I)^{-1}J_R^TR(x_k)
\]
- 加上一个 \(\lambda I\) 能够保证矩阵正定可逆
- \(\lambda\rightarrow0\) 完全牛顿法,收敛快
- \(\lambda\rightarrow\infty\) 完全最速梯度下降,下降快
- LM = GD + Gauss-Newton
Robust Estimation#
Local Minimum and Global Minimum#
如何尽量得到全局最优解
- 多初始化几次
- 将一个有最优解的近似情况的解作为初始猜测解
- 转换/近似为凸优化问题,凸优化可以保证局部最优就是全局最优
Outliers#
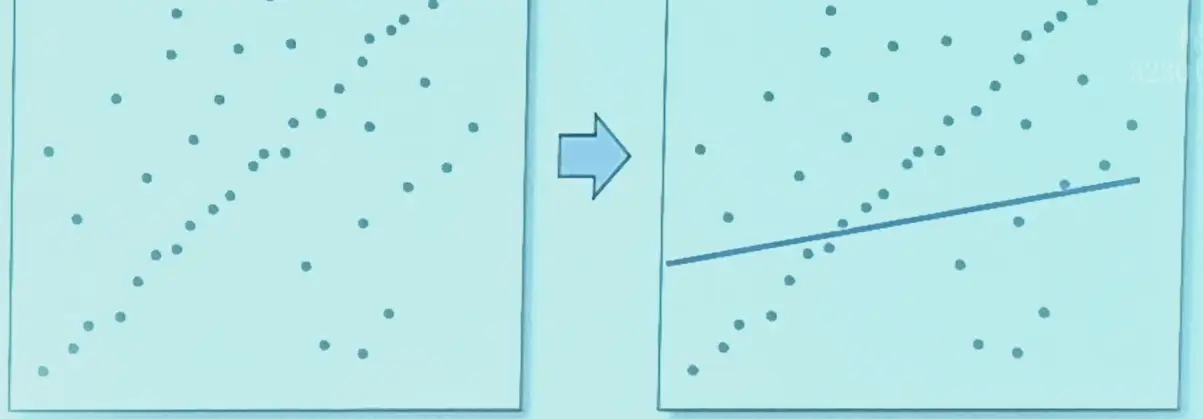
- outlier 可能权重过大,会导致结果偏差
- MSE 对 outlier 过于敏感
Robust Loss Function#
- 可以换其他目标函数,例如 L1 loss
- Huber loss,在 0 附近连续,绝对值较大时接近 L1
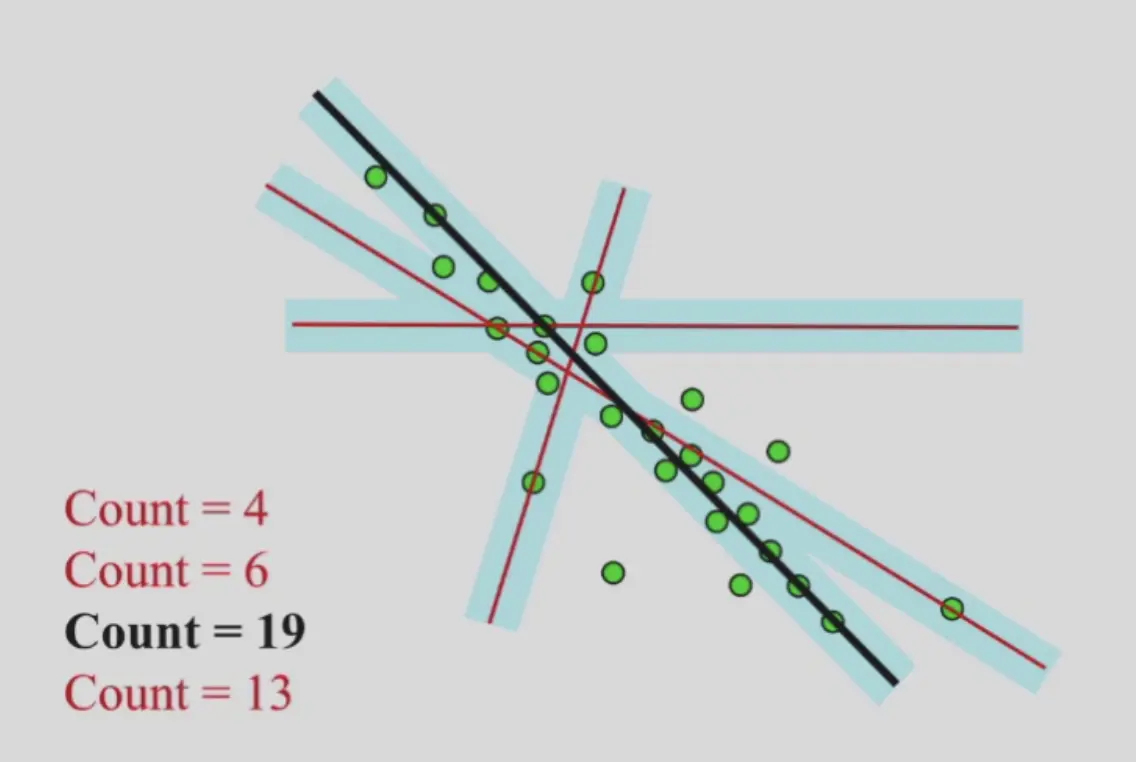
RANSAC#
Random Sampling Consensus
随机选择,进行投票
Overfitting and Underfitting#
- ill-posed problem: 模型参数太多,多于观测数据,很多解
- prior knowledge 能够加入一些约束
- e.g. 正则化 \(s.t. ||x||_2\leq 1\),或者直接加入到目标函数中
- 约束 L1 正则的时候,多数无效的参数都会严格变为 0,相当于模型变得稀疏,减少参数量