Final Questions
15-16 春夏#
Speed Check#
- With the same operations,

- Bin Queue deletemin 是 O(log N) 的
- neighborhood 里的搜索也可能需要指数时间!
- Max-cut approximation

- A 更新梯度,对的
- B 是 \(2|V|\log W\),错了
- least number of degree 2 node in B+ tree

- 如果全都是三度的,容量是 18 到 27 个,于是就可以满足,不需要任何二度节点
- most number of deg 2 node in B+ tree

- 可以构造尽量多的叶子,然后 bottom up 尽量都用 deg 2 节点建树
- about skew heap

- Skew heap 的最差合并复杂度是 O(N) 的
Stop and Think#
普通堆的均摊开销#

Tip
T
- delete 的总次数一定小于 insert 的总次数
- 无论如何均摊,只要保证 insert 的开销是大于等于 log n 就行,这样就是合理的,delete 的均摊开销甚至可以是 0
- 即均摊后的总和开销一定大于等于真实开销
- 另一方面,如果说 insert 是 1 而 deletemin 是 0 就是不合理的
3-SAT Random#

Tip
B 根据中心极限定理,应该是大约 0.5 C 一定存在,如果 clause 之间共享的变量不多,那么这种 assignment 显然存在;就算全都共享一样的变量,最差也有 ⅞
Which is true?#

Tip
C 正确的,因为可以执行很多次 D 不对,可以比最小的一个还要小,比如翻杯子问题,由于豆子已经确定在一个杯子里,总有一种算法只需要执行一次就能检查到
16-17 春夏#
Speed Check#




- 考虑长方形,近似比和初始猜测解有很大关系!!


- B 没问题,因为近似比的 2 就是这样证明出来的
- C 应该满足中心极限,接近 ½
Stop and Think#
skew heap 的精确复杂度计算#

Tip
- \(\Delta \Phi=k_{3}-k_{2}-k_{1}\)
- \(c=2+k_{1}+k_{2}+\lfloor \log n_{1} \rfloor+\lfloor \log n_{2} \rfloor\)
- \(\hat{c}=c+\Delta \Phi=2+k_{3}+\lfloor \log n_{1} \rfloor+\lfloor \log n_{2} \rfloor\leq 2+\lfloor \log n \rfloor+\lfloor \log n \rfloor+\lfloor \log n \rfloor\)?反正大致这样就能推出来 3
17-18 春夏#
Speed Check#



- 需要强调 high probablity

- log N,每次期望删掉一半
Stop and Think#
Set Cover Problem#

Tip
\(O(\log n)\)-factor approx
Which are true?#
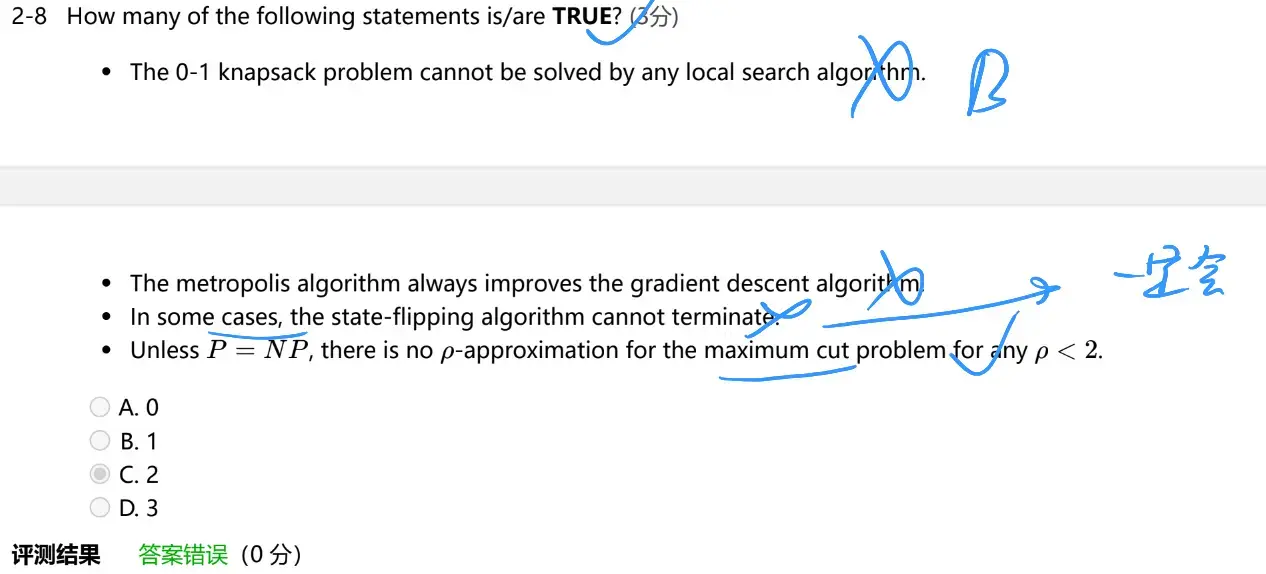
Tip
这里其实没有一个对的,因为 max-cut 有 1.1382 近似比
18-19 春夏#
Speed Check#

- 记住 \(log_k N+1\)



- 矩阵分块的复杂度是一样的,除非使用 winograd

- 这是对的,这里说的是整个算法得到的结果是一个局部最优,那么 p 肯定是更加优化的

- A 正确是因为染色一次就多一个黑色节点

- 逆否命题问题
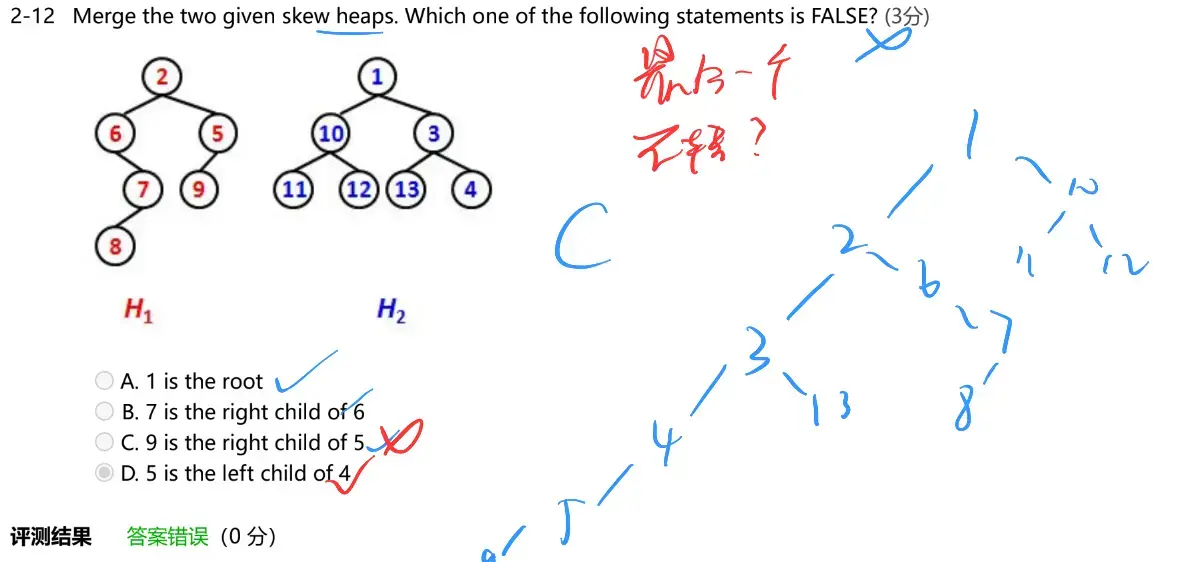
- 最后一个不转
19-20 春夏#
Speed Check#

- 纯纯眼高手低,应该是线性而不是平方的

- 这里先入为主了,目标不是减少 pass(那个是 polyphase merge),而是实现并行


- 这里 36 其实应该刚好相等?但是就是更快?可能是常数也会更小?
Stop and Think#
Vertex Cover Greedy#

Build RBT#
Tip
应该是 O(N) 的,一方面普通建堆也是 O(N) 的,另一方面,考虑第一次有 nlog2/2 第二次 nlog4/4 第三次 nlog8/8,就是 n 乘上一个 ½+2/4+⅜+4/16... 而这个数列很明显是收敛的,所以是常数
Minimum Degree Spanning Tree#

Tip
C A 除非是近似,不然一定是 1.5 的 lower bound,否则 P=NP D 是存在的 C 一看就觉得不太对,但是资料也查不到)
MAX-SAT#

Tip
B 是明显错误,应该是 8/7-approx
20-21 春夏#
Stop and Think#
Minimum Degree Spanning Tree Potential Func#

Answer
D A 显然错误,无环图的 degree 总和是 \(2|V|-2\) B 也有问题,进行一次操作后,删除的边 \(-(\geq d(w))\),但是增加了一条 \(d(u)+1\) 的边(假设 \(d(u)>d(v)\)),并且还有两条边可能 \(+2\),无法保证递减 C 有问题,对于操作中的 \(u,v,w\) 是满足的,实现了 \(-1\),但是可能导致其他很多点对的值变大 D 正确,进行一次操作,考虑 \(w\) 减少 \(-(\geq 2 \cdot 3^{d(w)-1})\),考虑 \(u,v\) 增加 \((2\cdot 3^{d(u)}+2\cdot 3^{d(v)})\)。假设 \(d(u)\geq d(v)\),存在 \(d(w)-1\geq d(u)+1\),所以整体递减,满足题意
2 item sizes bin packing#

Tip
只有 FF 有提升,NF 没有提升 期中 NF 没有提升是很好证明的,但是 FF 有提升需要及
21-22 春夏#
Speed Check#

- 举例子,例如一个两节点的和一个一节点的,原本 max npl 是 0,但是合并后可以变成 1 找最简单的例子就行
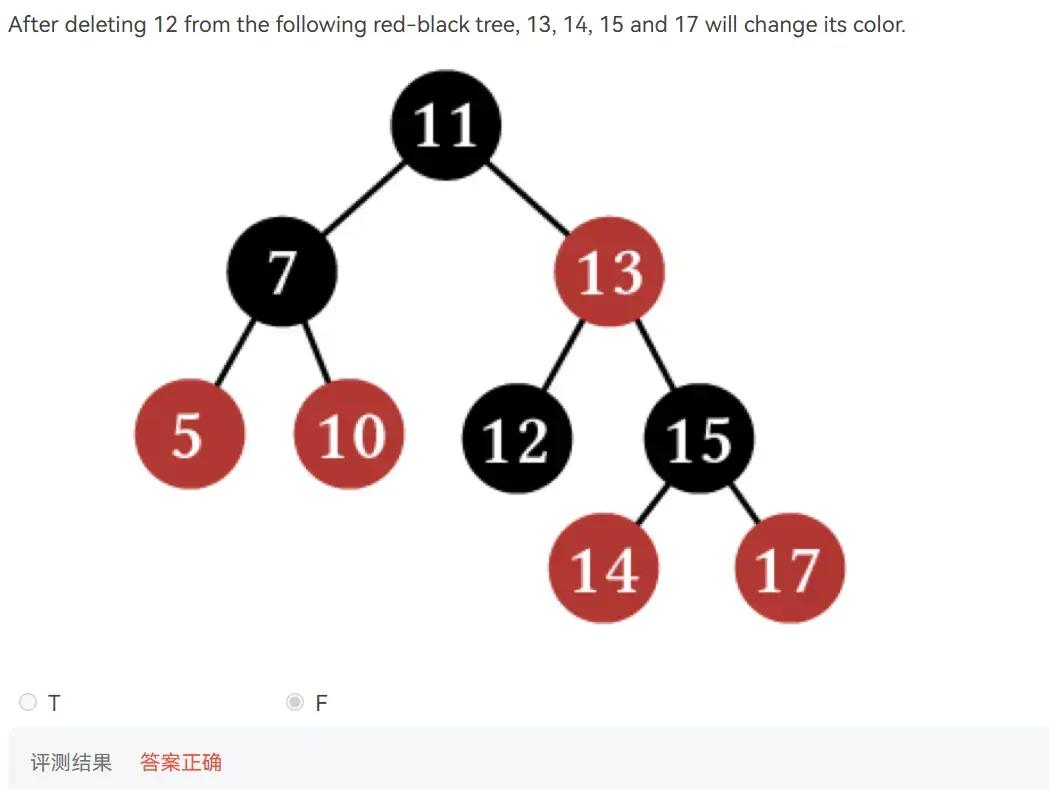
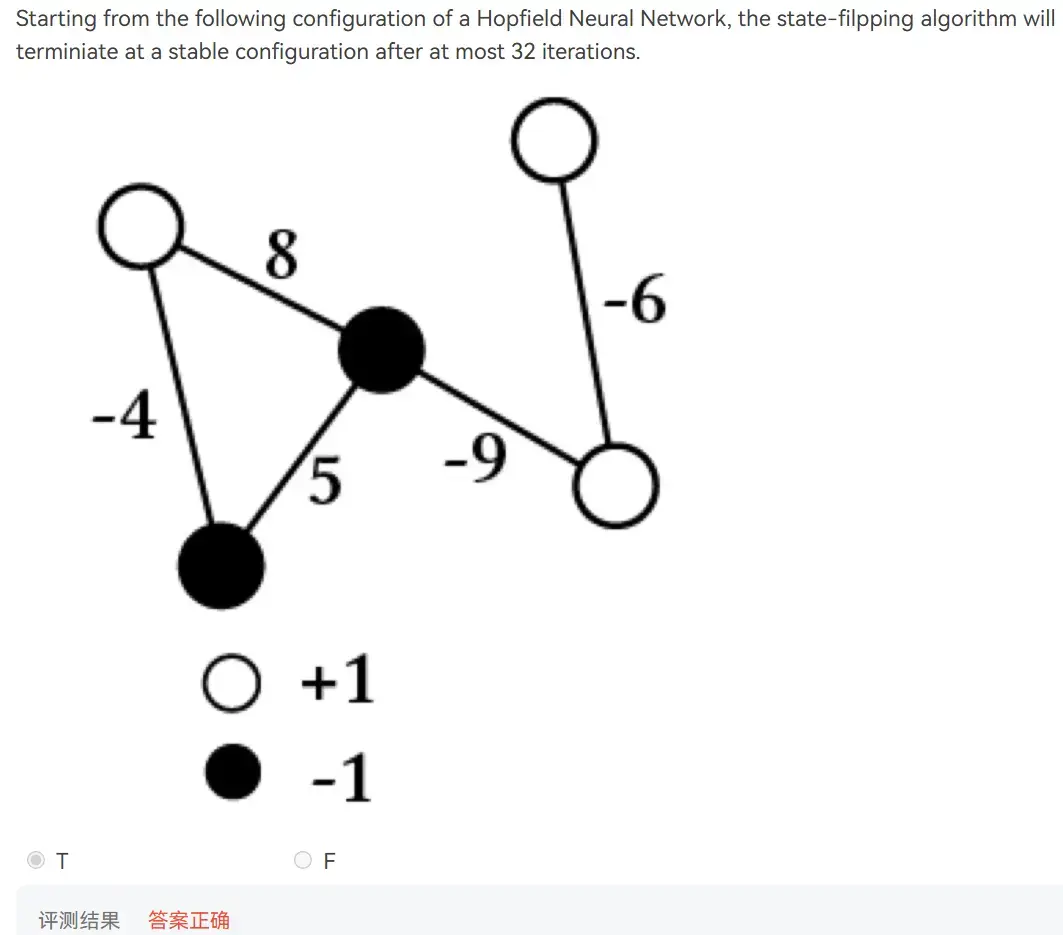
- 所有边的权重绝对值和
- 不存在,Quick sort 最好也是 nlogn 的

Stop and Think#
\(\sqrt{ n }\)-paradigm merge sort#
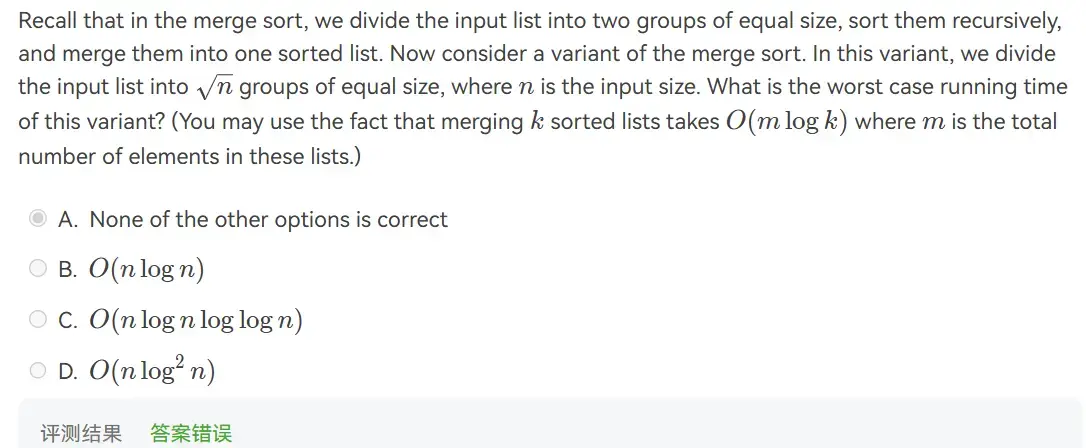
Tip
- 这里的 m 是所有列表中的总元素个数,千万要仔细读题!!
- 这样的话,就有 \(T(n)=\sqrt{ n }T(\sqrt{ n })+n\log \sqrt{ n }\)
- 使用代入检验,就能得到 B