Skip to content

11 Approximation

1 Intro#

Tip

To deal with HARD problems

Find near-optimal solution in polynomial time is Approximation

1.1 Approximation Ratio#

  • \(C^*\): 最优解
  • \(C\): 近似解
  • \(\rho(n)\): Approximation Ratio
\[ \max(\frac{C}{C^*}, \frac{C^*}{C})\leq \rho(n) \]

如果某个算法满足上面的式子，则可以称为 \(\rho(n)\)-approximation algorithm

1.2 Approximation Scheme#

一类近似算法，对于输入和给定的 \(\epsilon\) 值，是一个 \((1+\epsilon)\) 近似算法

  • PTAS 多项式时间近似方案 \(O(n^{f(1/\epsilon)})\)
    • \(O(n^23^\varepsilon)\) 也是 PTAS
  • FPTAS 满多项式时间近似方案 \(O(n^{O(1)}(\frac{1}{\epsilon })^{O(1)})\)

1.3 算法设计目标#

  • Optimality
  • Efficiency
  • All instances 全部实例，指的是应用的广泛性

2 Bin Packing Problem#

2.1 Online Algos#

按照顺序遍历所有物品，称为 online

2.1.1 Next Fit 2-approx#

  • 每次看下一个能不能放进当前的箱子，如果不能就新建一个箱子

  • 一定有 \(M\leq 2M^*-1\)

    • 补充：如果最大物品的大小为 \(\alpha\)，那么近似比应该为 \(\(\rho=\begin{cases}\frac{1}{1-\alpha}&,0\leq \alpha\leq \frac{1}{2}\\2&,1/2<\alpha<1\end{cases}\)\)

  • \(O(N)\)

2.1.2 First Fit 1.7-approx#

  • 每次找到第一个能放进去的箱子，并放入；如果找不到，就新建一个箱子
  • \(M\leq 1.7M^*\)
    • 能够证明 \(M\leq 1.7M^*\)，而且存在一种输入使得 \(M=1.7(M^*-1)\)
  • 可以用数据结构优化，得到 \(O(N \log N)\) 的时间复杂度，每次找箱子的速度是 \(O(\log N)\)

Note

如果在原始的物品集合 \(L\) 中删除一个元素，那么可能导致解变差

2.1.3 Best Fit 1.7-approx#

  • 每次将物品放入现存的、能够容纳它的，且放入后剩余空间最小的箱子；如果找不到，添加新的箱子
  • \(O(N \log N)\)
  • 和 FItst Fit 一样是 1.7-approx 的

Note

可以构造一种特例，让上述的 Online Algos 都一定无法产生 \(M\leq \frac{5}{3}M^*\)

2.2 Offline Algos#

先将物品从大到小排序，找到 trouble maker，然后使用 FF 或 BF，类似贪心算法的思想

2.2.1 First Fit Decreasing#

  • \(M\leq\frac{11M}{9}+\frac{6}{9}\)，存在某种输入使之取等
  • \(FFD(L)\leq\frac{3}{2}OPT(L)\) 用分段函数就能简单证明
    • 其中 ⅔ 是最小的因数，除非 \(\text{P}=\text{NP}\)

3 Knapsack Problems 背包问题#

3.1 Fractional Version#

小数版本的，\(x_{i}\in[0,1]\)，物品是连续的如大米和水

  • 按照价值密度从高到低排序
  • 贪心，先放密度高的，得到最优解

3.2 0-1 Version#

只能放或者不放，即 \(x_{i}\in\{0,1\}\)，

  • NP-H 问题
  • 贪心法是一个 2-approx 算法
    • taking maximum profit/profit density

更明确的边界？

\(P_{\text{greedy}}\geq P_{\text{opt}}-p_{\max}\)

3.2.1 DP Algo#

  • 令 \(dp[i][p]\) 是前 \(i\) 个物品，总价值为 \(p\) 的情况下的最小质量

  • \[dp[i][p]=\begin{cases}\infty &i=0\\dp[i-1][p]&p_{i}>p\\ \min\{dp[i-1][p],w_{i}+dp[i-1][p-p_{i}] \}&\text{otherwise}\end{cases}\]
    • 分别代表了，不可能达到
    • 不取物品 \(i\)
    • 取物品 \(i\)
    • \(O(N^2p_{max})\)
    • 如果有 \(p_{max}<N^C\)，那么就可以说是多项式时间
    • 否则 \(p_{max}\) 可能是指数级的大小

改进对于 \(p_{max}\) 比较大时的效率

只保留 profit 的高位，会损失一定精度，有 \((1+\epsilon)P_{alg}\leq P\)

4 K-center Problems#

Question

给 \(n\) 个地址，需要选择 \(K\) 个中心点，最小化到最近中心点距离的最大值

4.1 Naive Greedy#

  • 第一个放在所有地址的重心
  • 后面每个都放在能使得 \(r_{max}\) 减小的位置

Warning

如果有两团离得很近的地址，而且 \(K=2\) 第一个中心点会被放在中间位置，得到非常差的解

4.2 Better Greedy#

  • 将中心点放在地址上，如果最优的最大距离为 \(r^*\)，能够保证这个中心点周围 \(2r^*\) 的范围能够覆盖最优解中的一个圆
  • 对于给定的 \(r\)，我们可以判定是否存在满足要求的 \(K\) 个中心点
  • 根据 \(0<r<r_{\max}\)，可以通过二分查找的方式找到最优的 \(r\)，即：如果对于某个 \(r\) 能够找到 \(K\) 个中心点，说明 \(r\) 过于宽松，可以减小；反之亦然
  • \(O(\log r_{\max})\)
  • 具体操作：随机选择第一个地址，删除它和它周围 \(2r\) 距离内的所有点，并重复这个操作

进一步优化？

  • 选择下一个中心点时，可以尽量选择距离上一个较远的地址
  • 但仍然是 2-approx

4.3 Polynomial 2-approx#

  • 可以证明，不存在多项式时间的 \((2-\epsilon)\)-approx 算法
  • 归谬法：
    • 如果存在多项式时间的 \((2-\epsilon)\)-approx 算法，那么也能在多项式时间内解决支配集 (Domination Set) 问题，这是一个 NPC 问题
    • 因此，除非 \(\text{P}=\text{NP}\)，否则不存在这样的算法

5 Discussion#

The FFD algorithm for bin packing achieves the following bounds:
FFD(L)≤(11/9)OPT(L)+1, for all L.

(1) Please show that FFD(L)≤(3/2)OPT(L), for all L, with the above inequality.

(2) Prove that the factor 3/2 is the best possible unless P=NP (note that deciding if two bins are sufficient to accommodate a set of items is NP-complete).

Partition Problem 是 NP 问题。如果物品总质量为 2，那么相当于一个 Partition 问题，于是 Partition 问题能够归约到装箱问题

如果 \(\rho(n)\leq\frac{3}{2}\)，

6 Questions#

6.1 HW11#

6.1.1 better approximation#

Suppose ALG is an \(\alpha\)-approximation algorithm for an optimization problem \(\Pi\) whose approximation ratio is tight. Then for every \(\epsilon>0\) there is no \((\alpha-\epsilon)\)-approximation algorithm for \(\Pi\) unless \(P=NP\). (T/F)

Answer

F. Tight 表示的是这种算法的 approximation 分析已达下界，但不表示其他算法不会比这个近似好，这两者之间没有任何关系。

6.1.2 different cost assessment#

As we know there is a 2-approximation algorithm for the Vertex Cover problem. Then we must be able to obtain a 2-approximation algorithm for the Clique problem, since the Clique problem can be polynomially reduced to the Vertex Cover problem.

Answer

F

Vertex Cover Problem，选择最少的顶点集合 \(S\)，使得所有边都与 \(S\) 中的顶点连接，即覆盖所有的边 NP-C Clique Problem(团问题)，团 (clique) 就是完全子图，在无向图中找到最大的完全子图 NP-C, NP-H

Clique Problem \(\leq_{p}\) Vertex Cover Problem 将 Clique Problem 中的图 \(G\) 转换为补图 \(G'\)，然后在 \(G'\) 上做 Vertex Cover，对于所有没有被选中的顶点，一定都如下图所示 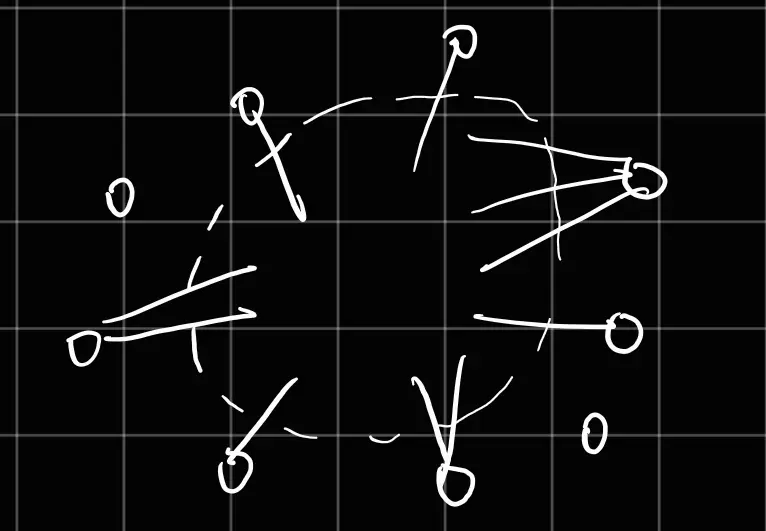__assets/ADS 11 Approximation/IMG-ADS 11 Approximation-20241121134722826.webp 所以，\(|V|-|S|\) 是一个完全子图，也就是 clique 的近似

但是，虽然 Vertex Cover Problem 中有 2- 近似算法能够得到 \(\rho_{2}=\frac{C_{2}}{C_{2}^*}=\frac{|S|}{|S^*|}=2\)，但是 Clique Problem 中的计算方式不一样：

\[ \rho_{1}=\frac{C_{1}^*}{C_{1}}=\frac{|V|-|S^*|}{|V|-|S|}=1+\frac{1}{\frac{|V|}{|S^*|}-2} \]

于是 \(rho_1\) 是不可确定的 1

6.1.3 approximation of TSP#

Question

__assets/ADS 11 Approximation/IMG-ADS 11 Approximation-20241121143321165.webp

1
2
3
4
5
Compute a minimum spanning tree T connecting all the addresses.
Regard the post office as the root of T.
Start at the post office.
Visit the addresses in order of a _____ of T.
Finish at the post office.
Answer

pre-order traversal/post-order traversal 2 首先，可以保证 MST 的总权重 \(M\) 一定小于任何一个 Hamilton 回路 (包括 \(C^*\))
其次，按照 pre-order 或者 post-order 进行遍历，最差情况就是需要经过 MST 的每一条边两次，即 \(C\leq 2M\)
所以 \(C\leq 2C^*\)

6.2 Ex11#

6.2.1 2 distinct item sizes#

Consider the bin packing problem which uses a minimum number of bins to accommodate a given list of items. Recall that Next Fit (NF) and First Fit (FF) are two simple approaches, whose (asymptotic) approximation ratios are 2 and 1.7, respectively. Now we focus on a special class I2 of instances in which only two distinct item sizes appear. Check which of the following statements is true by applying NF and FF on I2. 问哪个的 approx ratio 有提升？

Answer

6.2.2 Which is false?#

Assume P≠NP, please identify the false statement.

  • B. In the minimum-degree spanning problem, we are given a graph G=(V, E) and wish to find a spanning tree T of G so as to minimize the maximum degree of nodes in T. Then it is NP-complete to decide whether or not a given graph has minimum-degree spanning tree of maximum degree two.
  • C. In the minimum-degree spanning problem, we are given a graph G=(V, E) and wish to find a spanning tree T of G so as to minimize the maximum degree of nodes in T. Then there exists an algorithm with approximation ratio less than 3/2.
Answer

C B 确实是 NP-C 的 C 不会证明

6.3 knapsack + packing#

多个背包，最大化总权重

使用任何如 NF, FF, BF 等的贪心算法，得到的近似比最小都是 2

Answer

T，可以

  1. 参考 Homework - Jianjun Zhou's Notebook ↩

  2. 参考 Travelling Salesman using Approximation Algorithm ↩

Comments