Skip to content

13 Randomized Algorithms

1 Intro#

1.1 Review#

  • NP-C: 很难的问题
  • approximation: 暴力算法的 baseline
  • local search: 局部最优的优化

1.2 Random#

  • 不同的随机算法
    • 具有较高的概率得到最优解
    • 总是能得到最优解，但是期望复杂度更低，类似 amortized
  • Symmetry-breaking among processes in a distributed system.
    • 相比之下，local search 在对称结构下可能陷入循环
特点 Monte Carlo Las Vegas
结果准确性 近似解 确定解
执行时间 确定 不确定

外层使用 Monte Carlo，内层使用 Las Vegas，可以确保在有限时间里总是得到正确解

2 Hiring Problem#

Question

连续面试 \(N\) 个人，每次面试开销 \(C_i\)，每次给当前最优的人一笔签名费 \(C_h\)，如果雇佣了 \(M\) 人，那么总开销是 \(NC_{i}+MC_{h}\)

2.1 Strategy 1#

每次都签比先前面试者都好的

worst case

按照水平递增的顺序来面试，全都签了

2.2 Strategy 2#

先随机打乱顺序，再进行 strategy 1

  • 随机排列 (permute)
  • \(E(P\{i \text{ is hired}\})=\frac{1}{i}\)
    • 对于一个数组，第 \(i\) 个数字刚好是前 \(i\) 个中最大的概率
  • 于是就有了对数关系 \(O(C_{h}\ln N+NC_{i})\)

2.2.1 Permute Algo#

如何 permute 一个数组

  • 给每一个元素赋予一个随机数
  • 按照这个随机数进行排序
  • 产生的是均匀随机排列 (uniform random permutation)

2.3 Strategy 3#

对于前面 \(k\) 个人，找到他们当中能力的最高值，但是并不会雇佣他们；然后对于后面的面试者，如果能力高于这个阈值，就雇佣并停止面试

  • \(i\,(i>k)\) 刚好是能力最优者且被雇佣的概率
    • \(i\) 能力最优 \(1/N\)
    • 雇佣 \(i\)，意味着前面的人都没被雇佣，也就是说前 \(i-1\) 个人中最优的在前 \(k\) 个，\(k/(i-1)\)
    • 所以概率为 \(\frac{k}{N(i-1)}\)
  • 雇佣到能力最佳的候选者的概率，就是 \(p=\sum_{k+1}^N \frac{k}{N(i-1)}\)
    • 根据积分结果得到不等式 \(\frac{k}{N}\ln(\frac{N}{k})\leq p\leq \frac{k}{N}\ln(\frac{N-1}{k-1})\)
    • 求导得到最佳的 \(k=\frac{N}{e}\)，而且雇佣到能力最佳候选人的概率至少为 \(\frac{1}{e}\)

Warning

无法保证找到最优解

Note

这种 online 算法中，如果雇佣了能力超过前 \(k\) 个人而继续寻找，预期雇佣人数为 \(\frac{N-k}{k+1}\)

3 Randomized Quicksort#

Quicksort

  • worst: \(\Theta(N^2)\)
  • average: \(\Theta(N\log N)\)

为了减少最坏情况出现的概率，需要对 pivot 的选择引入随机性

3.1 Central Splitter#

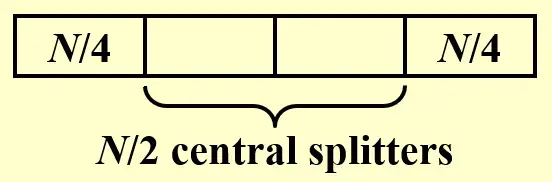
__assets/ADS 13 Randomized Algorithms/IMG-ADS 13 Randomized Algorithms-20241223003927260.webp

  • 寻找 central splitter
    • 保证改进后的 quicksort 始终能够选出一个 central splitter
    • 预期寻找 central splitter 的迭代次数为 2
  • 复杂度计算
    • 证明省略
      • 用 divide and conquer 来证明可以吗？
    • 时间复杂度是稳定的 \(O(N\log N)\)

4 Discussion#

4.1 Randomized Quicksort#

Question

Let's consider the Randomized Quicksort where each pivot is randomly chosen from the subsequence. The following is the pseudo-code:

1
2
3
4
5
6
7
8
9
RandQSort( A, L, R ) {
    if (L < R) {
        i = random(L, R);
        swap(A[i], A[R]);
        p = Partition(A, L, R);
        RandQSort( A, L, p-1 );
        RandQSort( A, p+1, R );
    }
}

Show that the expected running time is \(O(n \log n)\) for sorting \(A[1\dots n]\).

Hint: Partition is called \(n\) times. Each call takes a constant time plus the number of comparisons with the pivot. Hence the total run time is \(O(n+X)\) where \(X\) is the total number of comparisons with the pivots. You need to prove that \(E[X]=O(n\log n)\).

Assume the sorted array is \(R[1\dots n]\), and there exist \(r_i\) and \(r_j\) where \(i<j\) and \(r_i<r_j\).

If there has been a comparison between \(r_i\) and \(r_j\), then \(r_i\) or \(r_j\) should be the first chosen pivot out of \(R[i\dots j]\), (or \(r_i\) and \(r_j\) would be partitioned and would never be compared), whose probability is \(\frac{2}{j-i+1}\), which is also the expectation number of comparison happened between any two numbers.

Then, for all the number pairs \((r_i,r_j)\), add the expectation up:

\[ \begin{align} E(\text{\#comparisons})&=\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}\frac{2}{j-i+1} \\ &=O(\int_{1}^n\int_{i}^n \frac{1}{j-i+1}\, \mathrm{d}j\, \mathrm{d}i)\\ &=O(\int_{1}^n \ln(n-i+1)\,\mathrm{d}i) \\ &=O(n\ln n) \end{align} \]

Thus, the overall expected time complexity is \(O(n \ln n)\).

4.2 MAX 3-SAT Problem#

Question

Given a \(3\)-SAT formula with \(k\) clauses, in which each clause has three variables, the MAX 3-SAT problem is to find a truth assignment that satisfies as many clauses as possible. A simple randomized algorithm is to flip a coin, and to set each variable true with probability \(1/2\), independently for each variable.

Prove that the expected number of clauses satisfied is \(7k/8\). Hence if we repeatedly generate random truth assignments until one of them satisfies \(\ge 7k/8\) clauses, then this algorithm is a \(8/7\)-approximation algorithm.

A clause has 3 varibles, for example \((\neg x_{1} \vee x_{2} \vee \neg x_{3})\). For all truth assignments, the probability that one clause is true is:

\[ p=1-(\frac{1}{2})^3=\frac{7}{8} \]

Thus, if there are \(k\) clauses, for one assignment, \(E(\text{\# true clauses})=7k/8\).

The optimal solution can satisfiy \(n^*(\leq k)\) clauses. If one truth assignment satisfies \(n\geq 7k/8\). Then:

\[ \rho=\frac{n^*}{n}\leq \frac{8}{7} \]

Then this is a \(8/7\)-approximation algorithm.

4.2.1 More about#

  • 考虑 MAX 3-SAT Problem 最优解的性质
    • 如果约束非常多，例如 \(x_{1},x_{2},x_{3}\) 能构成的八个 clause 都出现，那么只能有 \(7/8\) 满足
    • 但是如果约束没那么多，肯定大于 \(7/8\)
    • 于是，对于任意的 MAX 3-SAT 问题，都一定能找到 \(\geq 7/8\) 的解

5 Questions#

5.1 Ex13#

5.1.1 Las Vegas and Monte Carlo#

A Las Vegas algorithm is a randomized algorithm that always gives the correct result, however the runtime of a Las Vegas algorithm differs depending on the input.
A Monte Carlo algorithm is a randomized algorithm whose output may be incorrect with a certain (typically small) probability. The running time for the algorithm is fixed however.
Then if a Monte Carlo algorithm runs in \(O(n^2)\) time, with the probability 50% of producing a correct solution, then there must be a Las Vegas algorithm that can get a solution in \(O(n^2)\) time in expectation.

Answer

T，可以使用这个 monte carlo 算法来构造一个 las vegas 算法，monte carlo 期望运行两次，如果 las vegas 反复调用 monte carlo 直到得到解，那么它也是 \(O(n^2)\) 的

5.1.2 Balls and boxes#

__assets/ADS 13 Randomized Algorithms/IMG-ADS 13 Randomized Algorithms-20241223113721265.webp

Answer

D

从箱子的角度，考虑一个箱子被几个球选中，比较方便思考，每个箱子被 \(X \sim B(m,\frac{1}{m})\) 个球选中

C 显然，有多少个空箱子，就有多少个 rejected balls，所以 C 正确 D \(1-(\frac{m-1}{m})^m-C_{m}^1 \frac{1}{m}(\frac{m-1}{m})^{m-1}=1-\frac{2}{e}\)

5.1.3 k-th Smallest Number#

__assets/ADS 13 Randomized Algorithms/IMG-ADS 13 Randomized Algorithms-20241223114819991.webp

Answer

Master theorm

\(T(n)\leq T(3n/4)+O(n)\) \(a=1,b=4/3,k=1\)，满足了 \(a<b^k\) 所以 \(O(n)\)

5.2 Q14#

5.2.1 Best in online hiring#

Consider the online hiring problem, in which we have total k candidates. First of all, we interview n candidates but reject them all. Then we hire the first candidate who is better than all of the previous candidates you have interviewed. It is true that the probability of the mth candidate is the best is \(\frac{n}{k(m-1)}\)​, where m>n.

Answer

T，这里的 best 指的是雇佣到最好的候选者

  • 最好的候选者在 \(m\)，概率为 \(1/m\)
  • 在上述情况下，雇佣到 \(m\) 的条件概率为 \(n/(m-1)\)，意味着前面 \(m-1\) 个人中最好的人被选到了前 \(n\) 个人里

5.2.2 MAX 3-SAT#

__assets/ADS 13 Randomized Algorithms/IMG-ADS 13 Randomized Algorithms-20241223122206273.webp

Answer

B C 这是正确的，即使约束最大，也能达到 \(7/8\) B 错误，因为期望就是 \(7k/8\)，概率不可能那么小，具体计算可能需要二项分布（或正态分布近似）

Comments