10 NP-Completeness

1 Intro

1.1 Recall: FDS

• 欧拉回路问题
• 哈密顿回路问题
• 单源无权最短路问题
• 单源无权最长路问题

其中，第一个和第三个比较容易解决，但是第二个和第四个没有已知的多项式时间算法

1.2 Formalization

Target

让不同问题的复杂度有一个统一的衡量标准

• inputs: binary 将所有类型的输入都统一成比特串，有利于统一时间复杂度表达和比较
• algo: Turing Machine
• outputs: True/False 所有的问题都可以转换成一连串的判定问题

Note

最简单的问题可以是 \(O(N)\) 的，因为至少也需要读入 input 最复杂的问题是不可判定问题 (undecidable problem)，无法用渐进符号描述

Undecidable Problem: Halting Problem

def g():
    if halts(g):
        loop_forever()          

• 如果 halts() 判定 g() 会停机，那么 g() 进入死循环
• 如果 halts() 判定 g() 不会停机，那么 g() 返回
• 这样就构造了一组矛盾，所以停机问题是不可判定的

2 NP, P, NP-H, NP-C

简称	全称	翻译	含义
P	Polynomial-time	多项式时间	能够在多项式时间 SOLVE 的问题
NP	Nondeterministic Polynomial-time	非确定性多项式时间	能够在多项式时间内 VERIFY 的问题
NP-C	NP-Complete	NP 完全问题	最难的一类 NP 问题 任何 NP 问题都能在多项式时间内归约到 NP-C \(\forall L \in\text{NP}, L\leq_{p}L' \in\text{NP-C}\)
NP-H	NP-Hard	NP 困难问题	如果一个 NP 问题 \(A\) 能够被归约到问题 \(B\)， 那么 \(B\) 比 \(A\) 更难且 \(B\) 是 NP-H 问题
Undecidable		不可判定问题	不存在有限时间算法的问题 不属于任何上述 complexity class

2.1 Turing Machine

• Infinite Memory
• 随机读写的 Scanner

• 控制 Scanner 移动和读写行为的 Rules

• Deterministic Turing Machine: 每一步的操作都由当前的指令唯一确定

• Deterministic Turing Machine: 每一步的操作可以从 finite set 中选择，总是选择能得到解的操作，lucky machine

Attention

Solvable 不一定意味着 decidable

#Algorithm/Problem/Post-Correspondence-Problem

一个有趣的 solvable yet undecidable 问题 Post correspondence problem - Wikipedia，通过将问题规约成 Turing Machine 来证明不可判定

和停机问题一样，PCP 是一个 undecidable 问题。

有一些 dominos，top 和 bottom 有不同的字符串，每个 domino 可以使用多次。

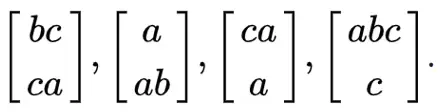
找到一种排列方式，使得 top string 和 bottom string 完全相同。

Solvability

• 找到一个 top bottom 第一个字母一样的 domino
• 以此类推，如果某个部分解 top bottom 不等长，找缺失的字母；如果部分解已经对齐，就得到了答案

但是可以找到这样的例子：

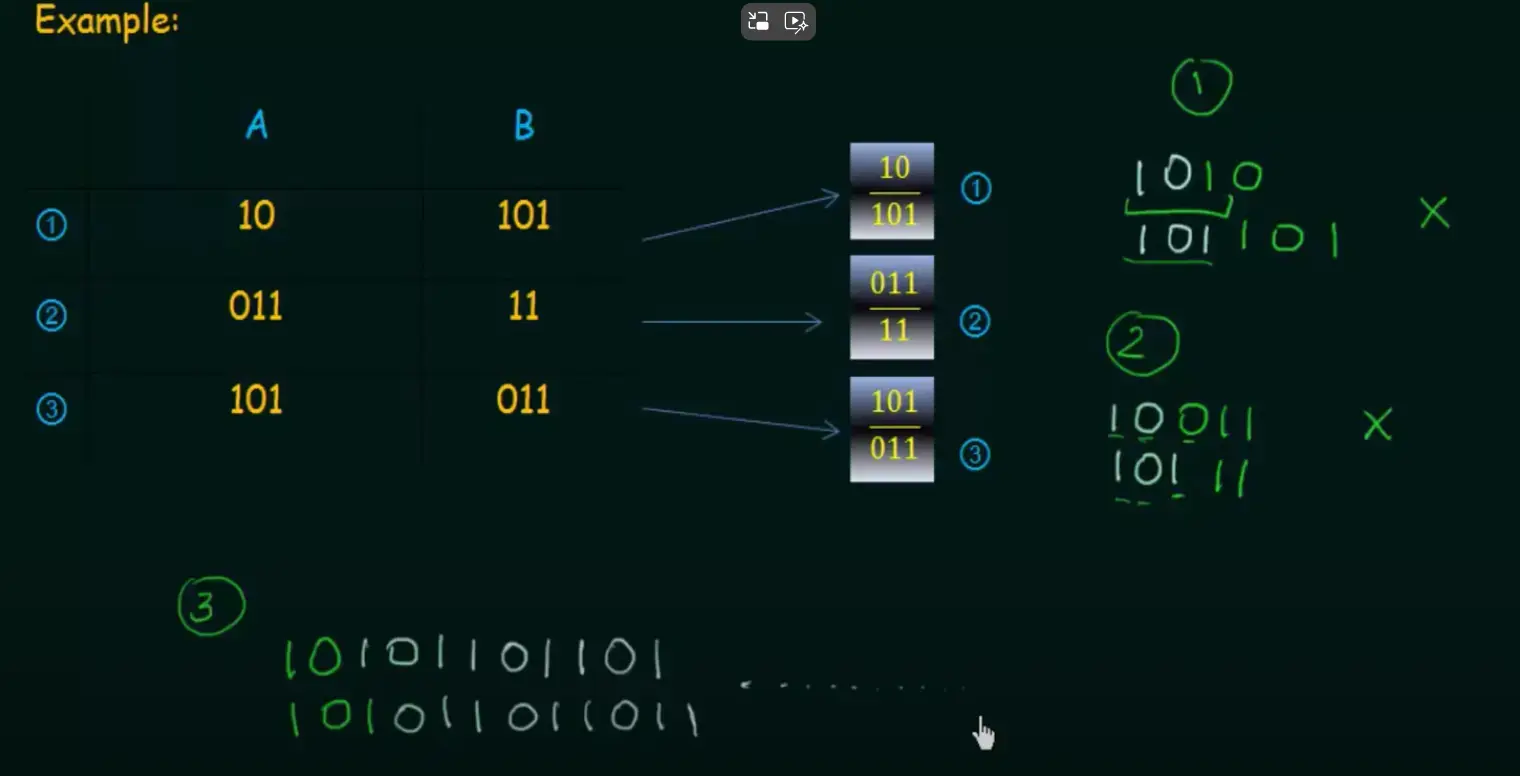其中，如果一直尝试配对，将一直放 3 号 domino 而不会停止

Undecidability

如果能将一个 undecidable problem 规约到 PCP，那么 PCP 肯定也是 undecidable 的 Undecidability of the Post Correspondence Problem 介绍了如何将 Acceptance Problem of a Turing Machine (命题接受问题，undecidable) 规约到 PCP 来完成证明

2.2 NP: Nondeterministic Polynomial-time

• 能在多项式时间内验证任何解是否正确的问题
• e.g. #Algorithm/Problem/Hamiltonian-Cycle

Attention

不是所有 decicable problem 都是 NP 问题 例如判定一个图是否有 Hamiltonian cycle，这个问题可以在多项式时间内解决；但是要 verify 就必须找出一个 Hamilton cycle，没有多项式时间算法能做到

但是 NP 问题全都是 decidable 的

2.3 Reduction

\(A\) 类问题的一个实例是 \(\alpha\)，如果存在一个程序能够在多项式时间内完成 \(R(\alpha)\to \beta \in\text{Problem }B\)，也就是将待解决的 \(\alpha\) 转换成了 \(B\) 类问题的实例 \(\beta\)，且对于 \(\beta\) 的解等价于对于 \(\alpha\) 的解，那么就完成了一次从 \(A\) 到 \(B\) 的规约，记作 \(A\leq_{p}B\)。

2.4 NP-H: NP-Hard

• 如果一个问题具有这样的性质：所有的 NP 问题都能在多项式时间内归约到它，那么这个问题就是一个 NP-H 问题
• NP-H 问题不一定是一个 NP 问题，它可能是无法在多项式时间内得到验证的
  • 例如 Halting Problem、优化版本的 TSP 问题（找到一条最短路而不是给出一条长度 \(\leq K\) 的哈密顿环）

2.5 NP-C: NP-Complete

• \(\text{NP-C}=\text{NP}\cap\text{NP-H}\)
• NPC 问题继承了 NP-H 问题的性质：所有的 NP 问题都能够在多项式时间内归约到它 \(\forall L \in\text{NP}, L\leq_{p}L' \in\text{NP-C}\)
• NPC 问题是 NP 中最难的问题，如果某个 NPC 问题能够在多项式时间内求解（\(\text{P}=\text{NP}\)），则所有 NP 问题都能在多项式时间内求解

2.5.1 Complexity Graph

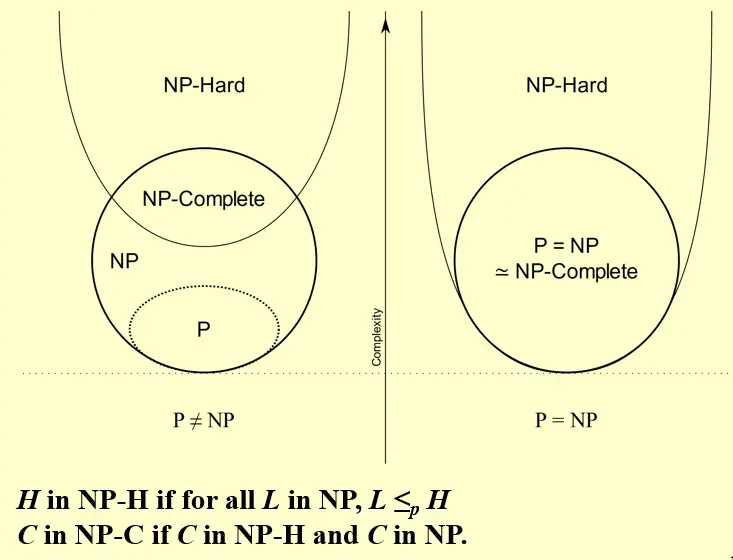
2.5.2 Example: Hamiltonian Cycle \(\leq_{p}\) TSP

• TSP: 对于给定的有权完全图，是否存在一个哈密顿环，使得其总权重 \(\leq K\)
• 只需要将 Hamiltonian Cycle 问题中存在的边赋为 1，不存在的边赋为 2，然后问 \(K=|V|\) 的 TSP 就好

2.5.3 NP-C Problems

• 第一个被证明是 NP-C 的问题是 Circuit-SAT 问题，对于一个给定的布尔表达式，问是否存在一种赋值方式能够使得表达式为真

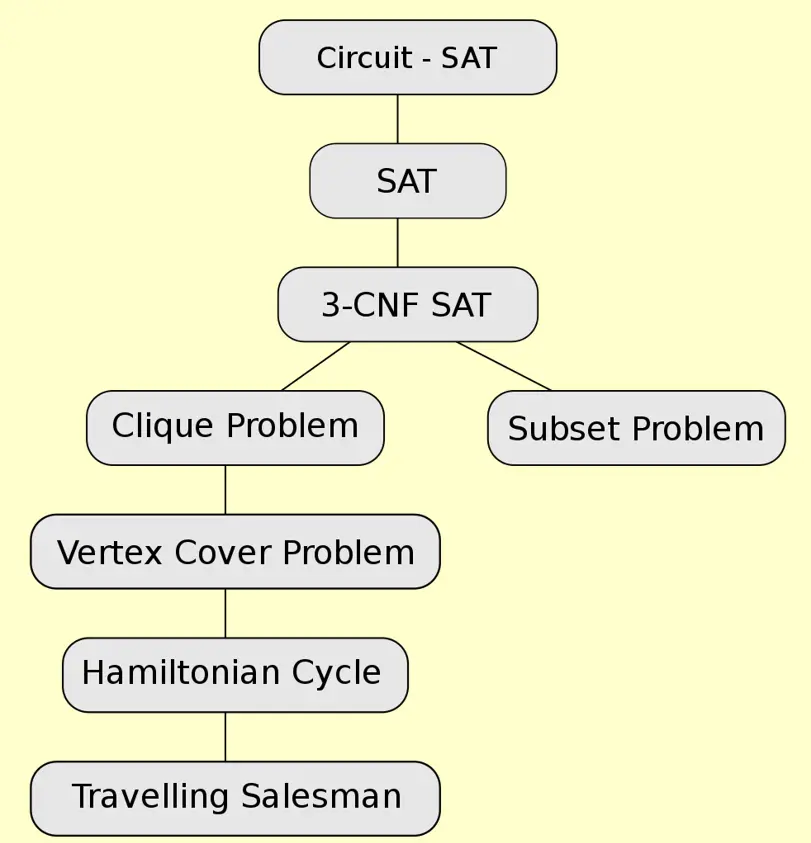
3 Formal Language

3.1 Abstract Problem

形式语言中，将问题分为 Abstract Problem 和 Concrete Problem，分别是抽象问题和具体问题 - 抽象问题 \(Q\) 是问题实例集合 \(I\) 和问题解集合 \(S\) 的二元对应关系 - 具体问题是对抽象问题的一种编码，将 \(I\) 映射到一个 bitstring 上，\(Q\) 就变成了具体问题

3.1.1 Examples

• \(\text{SHORTEST-PATH}\)
  • \(I=\{<G,u,v>:G=(V,E)\text{ is an undirected graph; }u,v\in V\}\)
  • \(S=\{<u, w_{1},w_{2},\dots,w_{k},v>:<u,w_{1}>,\dots,<w_{k},v>\,\in E\}\)
  • \(\forall i\in I,\text{SHORTEST-PATH(i)}=s\in S\)
• \(\text{PATH}\) 判定版本
  • \(I=\{<G,u,v,k>:G=(V,E)\text{ is an undirected graph; }u,v\in V\text{; }k\in N\}\)
  • \(S=\{0,1\}\)
  • \(\forall i\in I,\text{PATH(i)}=1\text{ or }0\)
• Encoding
  • Map \(I\) into a binary string \(\{0,1\}^*\)，则 \(Q\) 是一个具体问题

3.2 Formal-language Theory -for decision problem

使用形式语言来统一描述

3.2.1 符号表示

• 字母表 \(\Sigma\) 是一个有限符号集 e.g. \(\{0,1\}\)
• 语言 \(L\) 表示由 \(\Sigma\) 中的字符构成的字符串的集合
• 空字符串为 \(\epsilon\)，空语言为 \(\emptyset\)
• 包含所有从 \(\Sigma\) 得到的字符串的语言记为 \(\Sigma^*\)
• \(L\) 的补记为 \(\bar{L}=\Sigma^*-L\)
• 两种语言的拼接 (concatation) 记为 \(L=\{x_{1}x_{2}:x_{1}x_{2}:x_{1}\in L_{1}\land x_{2}\in L_{2}\}\)
• \(L\) 的克莱尼闭包 (Kleene closure) 为 \(L^*=\{\epsilon\}\cup L\cup L^2\cup L^3\cup\dots\)

3.2.2 判定问题

• 接受和拒绝：如果 \(A(x)=1\) 则算法 \(A\) 接受 (accept) bitstring \(x\in\{0,1\}^*\)；如果 \(A(x)=0\)，算法 \(A\) 拒绝 (reject) 了 bitstring \(x\)
• 判定：如果 \(L\) 的每一个 bitstring \(x\) 都能够被 \(A\) 接受或拒绝，那么称 \(L\) 能够被算法 \(A\) 判定

P 类问题的描述

\(\text{P}=\{L\subseteq\{0,1\}^*: \text{there exists an algorithm }A\text{ that decides }L\text{ in polynomial time}\}\) 所有存在能在多项式时间内得到判定的算法的语言

3.2.3 验证算法 Verification Algorithm

\(A(x,y)\)，其中 \(x\) 是输入 bitstring，\(y\) 是证书 (certificate)，其实也就是另一个 bitstring

• 如果对于 \(x\)，存在 \(y\) 使得 \(A(x,y)=1\) 成立，那么 \(A\) 能够验证 \(x\)
• 如果对于所有 \(L\) 中的 \(x\) 都满足上述条件，那么 \(A\) 能够验证 \(L\)

\(L\) 为 NP 问题的充要条件

存在一个多项式时间的双参数验证算法 \(A\) 和一个常数 \(c\)，使得

\(L=\{x\in\{0,1\}^*:\text{there exists a certificate }y\text{ with }|y|=O(|x|^c)\text{ such that }A(x,y)=1\}\)

其中的 \(|y|=O(|x|^c)\) 只是为了让解的长度不至于直接影响时间复杂度

这样，就能说算法 \(A\) 能在多项式时间内验证 \(L\) 的解的正确性

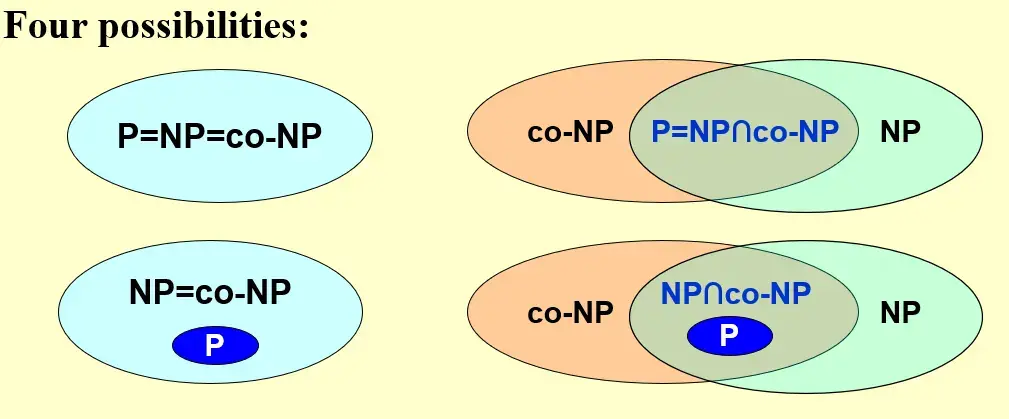
3.3 co-NP

如果已知 \(L\in\text{NP}\)，那么 \(\bar{L}\in\text{NP}\) 是否正确？

co-NP definition: 如果 \(\bar{L}\in\text{NP}\)，那么 \(L\in\text{co-NP}\)

3.4 Reduction Function

• 如果存在多项式时间可计算的函数 \(f:\{0,1\}^*\to\{0,1\}^*\) 能够实现 \(\forall x\in\{0,1\}^*, x\in L_{1}\Leftrightarrow f(x)\in L_{2}\)，那么 \(L_{1}\leq_{p}L_{2}\)
• 这样的函数 \(f\) 称为规约函数 (Reduction Function)
• 能够在多项式时间内计算出 \(f\) 的算法 \(F\) 称为规约算法 (Reduction Algorithm)

NP-C 的形式语言描述

\(L\in\text{NP}\) 且 \(\forall L'\in\text{NP},L'\leq_{p}L\)

3.5 Example: 证明 Vertex Cover Problem 是 NP-C 问题

已知 Clique Problem 是 NP-C 问题，证明 Vertex Cover Problem 也是 NP-C 问题。 思路是将 Clique 归约到 Vertex Cover

3.5.1 抽象问题表述

• \(\text{CLIQUE}=\{<G,K>:G\text{ is a graph with a clique of size }K\}\) #Algorithm/Problem/Clique
• \(\text{VERTEX-COVER}=\{<G,K>:G\text{ has a vertex cover of size }K\}\) #Algorithm/Problem/Vertex-Cover

3.5.2 证明过程

1. 证明 \(\text{VERTEX-COVER}\in\text{NP}\)
   • 对于 certificate \(y\)，检查一个图中所有的边是否都被 \(y\) 中的顶点覆盖
   • 遍历所有边，每次检查两个顶点中是否有一个在 \(y\) 中，最差的复杂度是 \(O(|E||V|)=O(|V|^3)\)
   • 所以 \(\text{VERTEX-COVER}\) 可以在多项式时间内验证，是 NP
2. 证明 \(\text{CLIQUE}\leq_{p}\text{VERTEX-COVER}\)，也就是一个大小为 \(K\) 的团的充要条件是 \(\bar{G}\) 有一个大小为 \(|V|-K\) 的顶点覆盖
   • 充分：取补图，则团内的顶点之间没有边；对于每条边，总有一个顶点是团外的顶点，所以取大小为 \(|V|-K\) 的团外所有顶点，一定构成一个顶点覆盖
   • 必要：没有被选择的 \(K\) 个顶点之间一定没有边，于是补图中能够构成大小为 \(K\) 的团

Tip

由于都是判定问题，只需要证明存在性即可，在充分性证明中不需要去讨论 \(|V|-K\) 是否为最小的顶点覆盖，在必要性证明中不需要去讨论 \(K\) 是否为最大的团

4 Concousion of Problems

Problem	Type	Complexity Class	Meaning	Reduction	Solvability	Decidability	Notes
SAT	Decision	NP-C	Satisfiability of Boolean formulas	Reduced to/from other NP problems	Solvable	Decidable	Basis of NP-completeness proofs
Circuit-SAT	Decision	NP-C	Satisfiability of Boolean circuits	Reduced to/from SAT	Solvable	Decidable	First NP-complete problem
3-CNF SAT	Decision	NP-C	SAT for 3-CNF formulas	Reduced to/from SAT	Solvable	Decidable	Special case of SAT
Clique	Decision	NP-C	Existence of a k-clique in a graph	Reduced to/from Vertex Cover	Solvable	Decidable	Graph theory problem
Subset	Decision	NP-C	Subset sum equals a target	Reduced to/from Knapsack	Solvable	Decidable	Equivalent to special cases of Knapsack
Vertex Cover	Decision	NP-C	Covers all edges in a graph	Reduced to/from Clique	Solvable	Decidable	Dual problem to Clique
Hamiltonian Cycle	Decision	NP-C	Cycle visits all vertices exactly once	Reduced to/from TSP	Solvable	Decidable	Graph traversal problem
TSP	Decision	NP-C	Visits all cities with minimal cost	Reduced to/from Hamiltonian Cycle	Solvable	Decidable	Optimization problem
Euler Cycle	Decision	P	Cycle visits every edge exactly once	Reduced to/from degree condition	Solvable	Decidable	Can be solved in polynomial time
Single-Source Longest Path	Decision	NP-H	Longest path in a weighted DAG	Reduced to/from other NP problems	Solvable	Decidable	Hard for NP, no known poly-time solution
Halting Problem	Decision	Undecidable	Program halts on input or not	Not reducible	Unsolvable	Undecidable	Fundamental undecidable problem
Knapsack	Decision	NP-C	Subset with target weight/value	Reduced to/from Subset	Solvable	Decidable	Basis for many cryptographic systems
Bin Packing	Optimization	NP-H	Pack items into minimum bins	Reduced to/from other NP problems	Solvable	Decidable	Approximation algorithms available
Domination Set	Decision	NP-C	Minimum dominating set in a graph	Reduced to/from Vertex Cover	Solvable	Decidable	Graph theory problem
Minimum Spanning Tree	Optimization	P	Minimum weight spanning tree	Reduced to/from Graph Connectivity	Solvable	Decidable	Solvable in polynomial time
Maximum Flow	Optimization	P	Max flow in a flow network	Reduced to/from Flow Conservation	Solvable	Decidable	Solvable in polynomial time
Bipartite Matching	Optimization	P	Maximum matching in bipartite graph	Reduced to/from Flow Problems	Solvable	Decidable	Solvable using Ford-Fulkerson or similar
K-Center	Optimization	NP-H	Partition vertices into k clusters	Reduced to/from Facility Location	Solvable	Decidable	Common in clustering problems
Graph Coloring	Decision	NP-C	Assign colors to vertices	Reduced to/from SAT	Solvable	Decidable	Classic graph problem
Set Cover	Optimization	NP-C	Cover all elements with subsets	Reduced to/from Vertex Cover	Solvable	Decidable	Basis for many optimization problems
Traveling Salesman Problem	Optimization	NP-C	Shortest tour visiting all vertices	Reduced to/from Hamiltonian Cycle	Solvable	Decidable	Different variants include approximation
Steiner Tree	Optimization	NP-H	Minimum tree connecting specified nodes	Reduced to/from MST	Solvable	Decidable	Harder version of MST
Partition Problem	Decision	NP-C	Split set into equal sum subsets	Reduced to/from Subset Sum	Solvable	Decidable	Special case of Subset Sum
Independent Set	Decision	NP-C	Maximum independent vertex set	Reduced to/from Vertex Cover	Solvable	Decidable	Related to Clique and Vertex Cover
Minimum Degree Spanning Tree	Decision	NP-C
Load Balancing Problem	Optimizatino	NP-H

5 Discussion

Question

A knapsack with a capacity \(M\) is to be packed. Given \(N\) items. Each item \(i\) has a weight \(w_i\) and a profit \(p_{i}\)​. An optimal packing is a feasible one with maximum profit.

This problem is NP-hard.

However, if no items have a size larger than \(N^2\), is it still NP-hard? Explain your answer.

给出一种 dp 算法，遍历所有物品，遍历所有 \(w=1,2,3,\dots,M\)，这样时间复杂度为 \(O(NM)\) 或 \(O(N^2W_{max})\)。

如果 \(\forall w, w\leq N^2\)，那么 \(W_{max}\leq N^3\)，所以变为多项式时间复杂度。

6 Questions

6.1 Midterm Review

6.1.1 NP-Completeness

Given that problem A is NP-complete. If problem B is in NP and can be polynomially reduced to problem A, then problem B is NP-complete. (T/F)

Answer

F 只能推导出 B is in NP，B 不一定能由其他所有 NP 问题在多项式时间内归化得到

6.1.2 Decidable languages

All the languages can be decided by a non-deterministic machine. (T/F)

Answer

F，存在不可判定问题

6.2 Ex10

6.2.1 Lanuage Reduction

Which one of the following statements is FALSE?

• A. A language \(L_1\) is polynomial time transformable to \(L_2\) if there exists a polynomial time function \(f\) such that \(w\in L_1\) if \(f(w)\in L_2\)
• D. If language \(L_{1}​\) has a polynomial reduction to language \(L_2\)​, then the complement of \(L_1\)​ has a polynomial reduction to the complement of \(L_2\)​.

Answer

A A 不是 if 是 iff D 将 \(f\) 取反，如果 \(x\not\in L_{1}\)，那么 \(f(x)\not\in L_{2}\)？

6.2.2 NP-C Problems?

Which one of the following statements is FALSE?

• A. SAT, Vertex Cover, Hamiltonian Cycle, Clique, Knapsack, Bin Packing, and Domination Set problems are all NP-completeness problems.
• B. If there is a polynomial time \((1+\frac{1}{2n})\)-approximation algorithm for Vertex Cover with n being the total number of vertices in the graph, then P=NP.
• C. If there is a polynomial time 3/2-approximation algorithm for K-Center, then P=NP.
• D. Given a weighted directed acyclic graph (DAG) \(G\) and a source vertex \(s\) in \(G\), it is NP-hard to find the longest distances from s to all other vertices in \(G\)

Answer

让我们逐一分析每个选项，找出其中的 FALSE 陈述。

---

选项 A

陈述：SAT, Vertex Cover, Hamiltonian Cycle, Clique, Knapsack, Bin Packing, and Domination Set 问题都是 NP- 完全问题。

分析：

• SAT（布尔可满足性问题）是第一个被证明的 NP- 完全问题。
• Vertex Cover（顶点覆盖问题）、Hamiltonian Cycle（哈密顿回路问题）、Clique（团问题）、Knapsack（背包问题）、Bin Packing（装箱问题）和 Domination Set（支配集问题）都是经典的 NP- 完全问题。

结论：该陈述是 TRUE。

---

选项 B

陈述：如果存在一个多项式时间的 \((1+\frac{1}{2n})\)- 近似算法（其中 \(n\) 是图中顶点的总数）来解决 Vertex Cover 问题，则 P=NP。

分析：

• Vertex Cover 是一个 NP- 完全问题。
• 已知 Vertex Cover 的近似算法的最小近似比为 \(2\)（即 2- 近似算法）。
• 如果存在一个比 \(2\) 更优的近似算法（例如 \((1+\frac{1}{2n})\)- 近似算法），则意味着可以在多项式时间内精确解决 Vertex Cover 问题，从而 P=NP。

结论：该陈述是 TRUE。

---

选项 C

陈述：如果存在一个多项式时间的 \(3/2\)- 近似算法来解决 K-Center 问题，则 P=NP。

分析：

• K-Center 是一个 NP- 完全问题。
• 已知 K-Center 的近似算法的最小近似比为 \(2\)（即 2- 近似算法）。
• 如果存在一个比 \(2\) 更优的近似算法（例如 \(3/2\)- 近似算法），则意味着可以在多项式时间内精确解决 K-Center 问题，从而 P=NP。

结论：该陈述是 TRUE。

---

选项 D

陈述：给定一个加权有向无环图（DAG）\(G\) 和一个源顶点 \(s\)，找到从 \(s\) 到所有其他顶点的最长距离是 NP- 难的。

分析：

• 在 DAG 中，最长路径问题（Longest Path Problem）可以在多项式时间内解决。
• 具体方法：对 DAG 进行拓扑排序，然后使用动态规划计算从 \(s\) 到每个顶点的最长距离。
• 因此，该问题不是 NP- 难的。

结论：该陈述是 FALSE。

---

最终答案

选项 D 是 FALSE。

6.3 Q11

6.3.1 All NP problems are decidable.

Answer

T 所有的 NP 问题都是可判定的，不可判定问题不存在 complexity class

Undecidable 不存在算法能够在有限的时间内解决的问题。

6.3.2 Proof of NP-C

To prove problem B is NP-complete, we can use a NP-complete problem A and use a polynomial-time reduction algorithm to transform an instance of problem B to an instance of problem A.

Answer

F 要证明的不止这些

1. B 是一个 NP 问题
2. 存在一个 reduction function \(f\)，能够将 A 中的任意实例转化为 B 中的实例，实现 \(A\leq_{p}B\)

7 Reference

• 高级算法入门必看—21个NPC问题及其证明-CSDN博客

Comments