Skip to content

14 Parallel Algorithms

1 Introduction#

  • Machine parallelism
    • multiple processors
    • pipelning
    • Very-Long Inst Word (VLIW)
  • Parallel algorithms

1.1 Models#

  • Parallel Random Access Machine (PRAM) 并行随机访问机
  • Work-Depth (WD) 工作深度

1.2 Basic concepts#

  • Unit time, 读写计算的操作都简化为单位时间
  • Shared memory, 所有处理器都使用同一块内存
vector_add
1
2
for Pi, 1<=i<=n pardo
    A(i):=B(i)

2 Conflicts#

step2\1 R W
R no conflict
W no conflict

2.1 Exclusive-Read Exclusive-Write (EREW)#

  • 完全不允许同时读写

2.2 Concurrent-Read Exclusive-Write (CREW)#

  • 同时读，分开写

2.3 Concurrent-Read Concurrent-Write (CRCW)#

  • 同时读，同时写
  • 同时写冲突解决
    • Arbitrary rule
    • Priority rule: 每个处理器分配一个权重，写入优先级高的
    • Common rule: 如果所有写入的值都一样，才允许同时写

2.4 Paralell find_max#

find_max
1
2
3
4
5
6
7
for i, j in [1, n], pardo
    if x[i] < x[j]:
        m[i] = 1
for i in [i, n], pardo
    if m[i] == 0:
        max = x
return max

利用了 common rule

  • \(\text{Depth}=O(1)\)
  • \(\text{Work}=O(N^2)\)
  • \(T=\text{Depth}=O(1)\)

3 Parallel Summation#

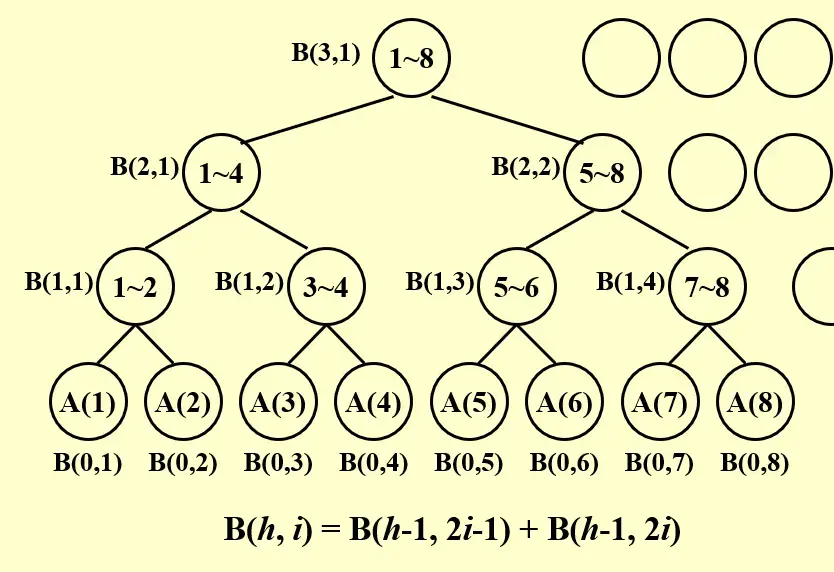
__assets/ADS 14 Parallel Algorithms/IMG-ADS 14 Parallel Algorithms-20241209135328356.webp

  • \(\text{Depth}=O(\log N)\)
  • \(\text{Work}=O(N)\)

3.1 PRAM Model#

PRAM Model
1
2
3
4
5
6
7
8
for i in [1, N] pardo
    B[0, i] = A[i]
for h=1 to log(N) do
    if i <= n / 2^h
        B[h, i] = B[h-1, 2*i-1] + B[h-1, 2*i]
    else stay idle

for i = 1: output B[log(N), 1]; for i > 1: stay idle

__assets/ADS 14 Parallel Algorithms/IMG-ADS 14 Parallel Algorithms-20241209141734817.webp

Bug

  • 无法揭示算法和实际使用的处理器个数之间的关系
  • 该模型需要指定哪个处理器处理哪部分的指令，这时就需要知道一些可能不太必要的细节，例如上面的 stay idle

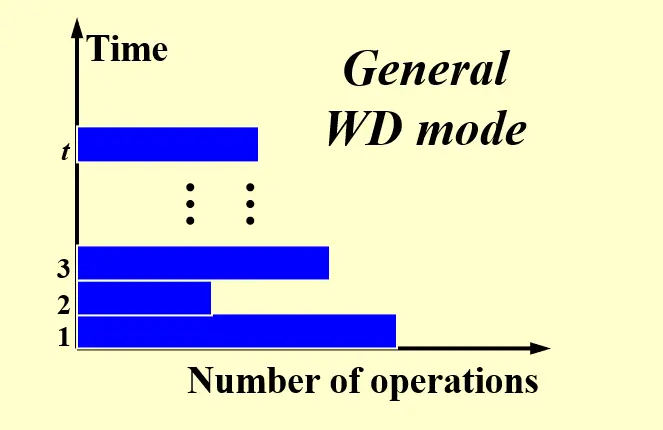
3.2 Work-Depth (WD) Presentation#

WD Model
1
2
3
4
5
6
7
for i in [1, n] pardo
    B[0, i] = A[i]
for h=1 to log(N)
    for i in [1, n/2^h] pardo
        B[h, i] = B[h-1, 2*i-1] + B[h-1, 2*i]
for i = 1 pardo
    output B(log N, 1)

Tip

这里与 PRAM 不同，不再显式地指出每个处理器应该干什么

__assets/ADS 14 Parallel Algorithms/IMG-ADS 14 Parallel Algorithms-20241209143120102.webp

4 Performance Measurement#

  • Work load \(W(n)\)
  • Running time \(T(n)\)

4.1 PRAM#

  • 将处理器个数与实际复杂度关联，其中的 \(T(n)\) 表示的是理想状态下（无限处理器个数）的 worst case time
    • PRAM: \(P(n)=W(n)/T(n)\) processors and \(T(n)\) time
    • PRAM: \(W(n)/p\) time using any number of \(p\leq W(n)/T(n)\) processors
    • PRAM: \(W(n)/p+T(n)\) time using any number of \(p\) processors
  • All asymptotically equivalent

4.2 WD#

Brent's Theorem

\[ \frac{W}{p}\leq T(n) \leq \frac{W}{p}+D \]

4.2.1 Discussion#

Question

Please prove that a parallel algorithm with workload \(W\) and depth \(D\) can be implemented in \(W/p+D\) time using \(p\) processors for any \(p>0\).

Assume that the workload on \(\text{depth}=i\) is \(w_{i}\).

In the worst case that each layer must be totally completed before executing any workload of the upper layer, we have \(t_{i}=\lceil w_{i}/p \rceil\), then:

\[ T=\sum_{i=1}^D t_{i}\leq \sum_{i=1}^D (\frac{w_{i}}{p}+1)=\frac{W}{p}+D \]

5 Prefix Sums#

Question

求一个序列所有的 \(n\) 个前序和

可以借助求和问题：假设我们已经有了求和的树状结构和每个 node 的值 B[h, i]，那么可以进一步求出 C[h, i] ，表示到其右叶子的前缀和

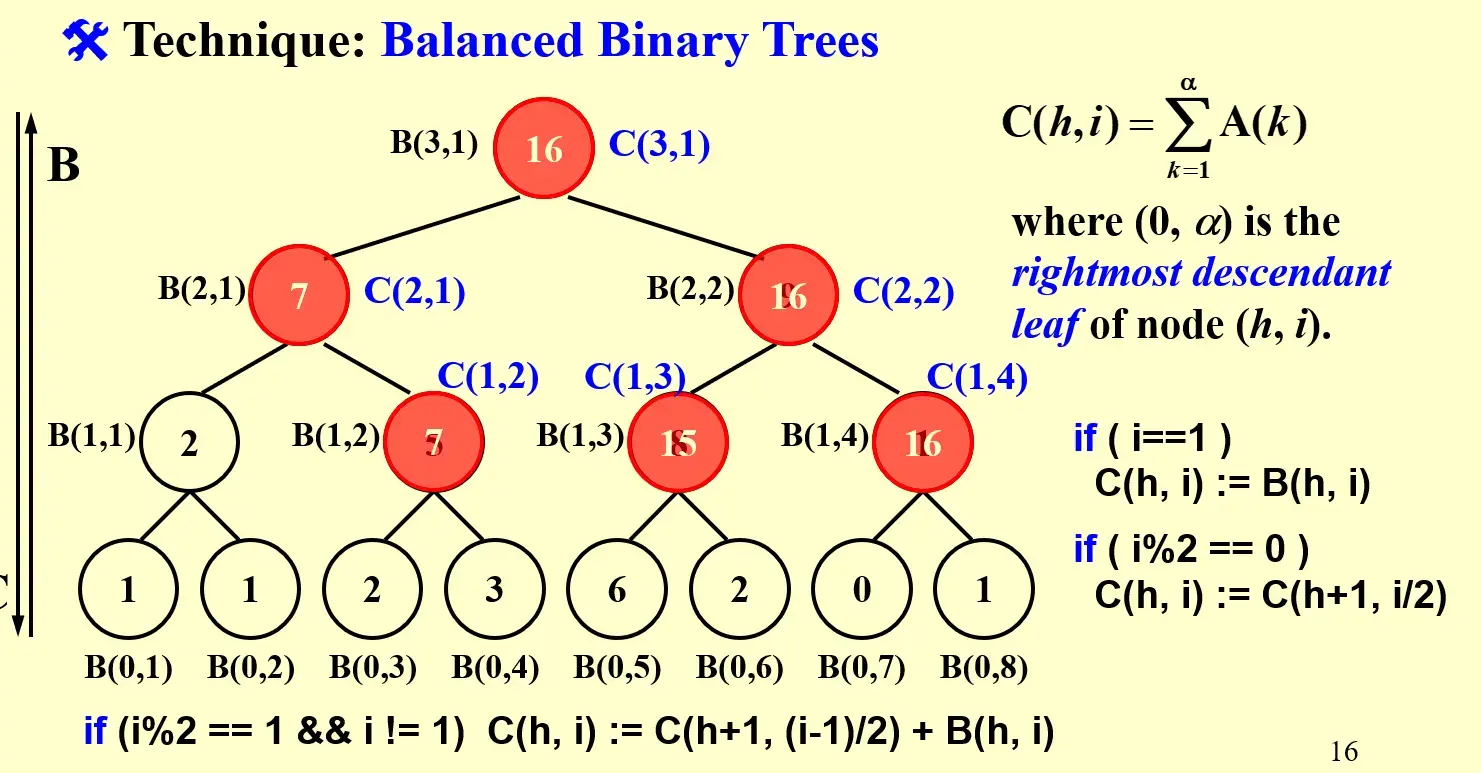
__assets/ADS 14 Parallel Algorithms/IMG-ADS 14 Parallel Algorithms-20241223005444998.webp

5.1 Implementation#

  • 首先，左路径上 C[h, 1] = B[h, 1]
  • 其次，每一层的偶数节点都等于父节点 if (1 % 2 == 0) C[h, i] := C(h + 1, i / 2)
  • 最后，计算除了左路径外的所有奇数节点，相当于其左上方节点的值加上自己的 B 值
    • if (i % 2 == 0 && i != 1) C[h, i] := C[h+1, (i - 1) / 2] + B(h, i)

Note

top-down，每一层都可以并行计算

5.2 WD Analysis#

  • \(T(N)=O(N \log N)\)
    • Prefix Sum 和 Summation 是一样难的
  • \(W(N)=O(N)\)

6 Merging#

将两个非递减的数组 \(A,B\) 合并到一个数组 \(C\)

进行下列简化

  • \(A,B\) 元素不重复
  • \(A,B\) 长度相等
  • \(\log n,\frac{n}{\log n}\) 均为整数

6.1 Partition#

  • 将较大的任务划分成很多独立的小任务
  • 并行执行这些小任务
  • 每个小任务用 serial algo 来解决

6.2 Ranking#

\[ \text{RANK}(j, A)=\begin{cases} i &\text{if }A(i)<B(j)<A(i+1), \text{for} 1\leq i<n \\ 0 &\text{if }B(j)<A(1) \\ n &\text{if }B(j)>A(n) \end{cases} \]
  • \(\text{RANK}(j,A)\) 表示元素 \(j\) 在非递减的 \(A\) 中的插入位置索引
  • 最终在 \(C\) 数组中的位置就是两个 RANK 之和
1
2
3
4
for P_i, 1 <= i <= n pardo
    C[i + RANK(i, B)] := A[i]
for P_i, 1 <= i <= n pardo
    C[i + RANK(i, A)] := B[i]

6.3 Ranking Methods#

6.3.1 并行二分查找#

  • \(T(n)=O(\log n)\)
  • \(W(n)=O(n\log n)\)

6.3.2 串行双指针#

  • \(T(n)=O(m+n)\)
  • \(W(n)=O(m+n)\)

6.3.3 Parallel Ranking#

假设 \(m=n\)，而且 \(A(n+1), B(n+1)\) 都比 \(A(n),B(n)\) 大

6.3.3.1 Stage 1: Partitioning#
  • 假设有 \(p=n/\log n\) 个处理器
  • 首先进行选择，以 \(\log n\) 为步长在两个数组中选择部分元素
  • 然后对选中的元素进行排序 下图中的箭头标记了插入位置
  • 转化成子问题 下图中部分标记为绿色

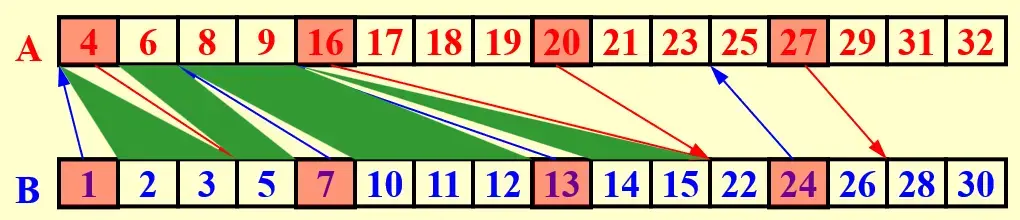
__assets/ADS 14 Parallel Algorithms/IMG-ADS 14 Parallel Algorithms-20241228121045932.webp

6.3.3.2 Stage 2: Actural Ranking#

最多得到 \(2p\) 个 \(O(\log n)\) 大小的子问题，分别进行串行排序

  • \(W(n)=\frac{2n}{\log n} O(\log n)=O(n)\)
  • \(T(n)=O(\log n)\)

7 Ultimate Parallel find_max#

no. type \(T\) \(W\)
a serial \(N\) \(N\)
b binary \(\log N\) \(N\)
c pair-wise brute-force \(1\) \(N^2\)
d.1 \(\log \log N\) \(N\log \log N\)
d.2 \(\log \log N\) \(N\)

7.1 A Doubly-logarithmic Paradigm#

假设 \(h=\log \log n\) 是整数，\(n=2^{2^h}\)。

7.1.1 \(\sqrt{ n }\) partition d.1#

每一层都用 \(\sqrt{ n }\) 进行分治，那么在每一层的 conquer 开销为：

  • \(T=C_{1}\)
  • \(W=C_{2}n\)

那么有

\[ \begin{align} T(n)&\leq T(\sqrt{ n })+C_{1} \\ W(n)&\leq \sqrt{ n }W(\sqrt{ n })+C_{2}n \end{align} \]

所以 \(T(n)=O(\log \log n),\,W(n)=O(n\log \log n)\)。

7.1.2 \(h\)-partition d.2#

第一层先用 \(h\)-partition，后面还是 \(\sqrt{ n }\)-partition；那么第一层分过之后，有 \(n/h\) 个大小为 \(h\) 的子问题，每个子问题有 \(T=O(\log \log (n/h)),\,W=O((n/h)\log \log (n/h))\)；最后再进行一个 \(T=O(h),\,W=O(h \cdot(n/h))\) 的 conquer：

\[ \begin{align} T(n)&=O(h+\log \log(n/h))&&=O(\log \log n) \\ W(n)&=O(h\cdot(n/h)+(n/h)\log \log(n/h))&&=O(n) \end{align} \]

7.1.3 Random Sampling d.3#

\(T=O(1),\,W=O(n)\), with very high probability, on an Arbitrary CRCW PRAM

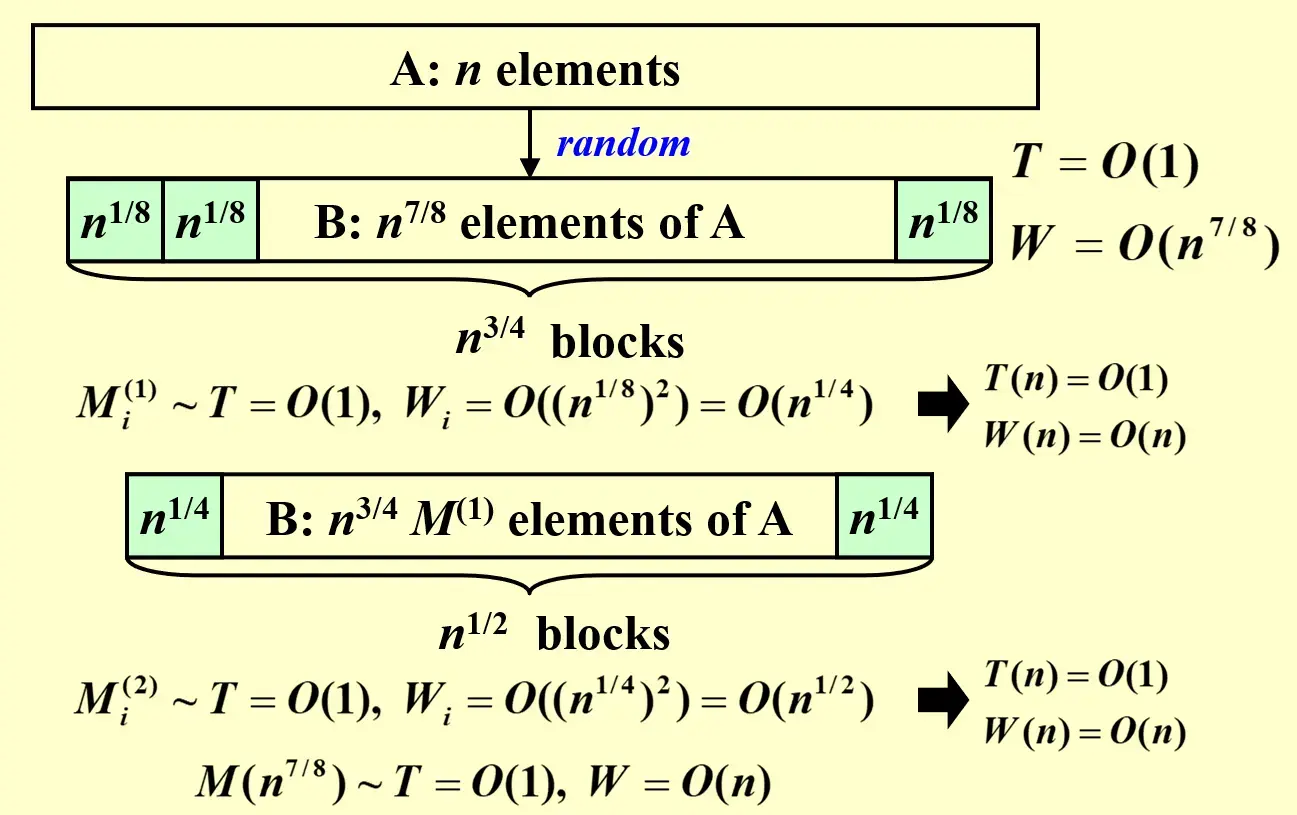
__assets/ADS 14 Parallel Algorithms/IMG-ADS 14 Parallel Algorithms-20241209153751412.webp

  1. 随机选择 \(n^{7/8}\) 个元素，分成 \(n^{3/4}\) 个大小为 \(n^{1/8}\) 的块
    • \(T=O(1)\)，可以并行选择
    • \(W=O(n^{7/8})\)
  2. 对这 \(n^{3/4}\) 个块进行并行 maximum finding
    • \(T=O(1)\)
    • \(W_{i}=O(n^{1/4}), W=n^{3/4}O(n^{1/4})=O(n)\)

  3. 然后，让 \(n\) 个处理器拿着找到的最大值与原来的 \(n\) 个元素进行比较，如果原来的元素比这个大的话就随机写入到一个长度仍然为 \(n^{7/8}\) 的数组中，再进行一次，直到找到最大值

  4. 得到正确结果的概率相当大，失败的概率为 \(O(\frac{1}{n^c})\)

8 Questions#

8.1 HW14#

8.1.1 Merge-sort complexity#

Sorting-by-merging is a classic serial algorithm. It can be translated directly into a reasonably efficient parallel algorithm. A recursive description follows.

MERGE−SORT( A(1), A(2), ..., A(n); B(1), B(2), ..., B(n) )

Assume that \(n=2^l\) for some integer \(l\ge 0\)

if n = 1 then return B(1) := A(1)

else call, in parallel, MERGE−SORT( A(1), ..., A(n/2); C(1), ..., C(n/2) ) and

  • MERGE−SORT(A(n/2+1), ..., A(n); C(n/2+1), ..., C(n) )
  • Merge (C(1),...C(n/2)) and (C(n/2 + 1),...,C(n)) into (B(1), B(2), ..., B(n)) with time O(n)

Then the MERGE−SORT runs in __ .

Answer

Merge 一次的时间开销是 \(O(\log n)\)，所以总体的时间开销应该是 \(O(\log^2 n)\) 题目中说 \(O(n)\) merge，但是这样的话早就 \(O(n)\) 了，估计是题目的问题

8.2 Q14#

8.2.1 W-D#

In Work-Depth presentation, each time unit consists of a sequence of instructions to be performed concurrently; the sequence of instructions may include any number. (T/F)

Answer

T, 定义就是这样说的，只要给定一个 unit 就行了，内部的操作数量任意

8.2.2#

Comments