02 Red-Black Trees and B+ Trees

1 Red-Black Trees

Target: balanced BST

1.1 Definition

1. 每个节点红或黑
2. 根是黑色
3. 每个叶子（NIL）都是黑色，NIL 是一个共享的没有 key 的叶子节点
4. 红色节点的两个孩子都是黑色，不能有两个连续的红色节点
5. 每个节点到叶子的路径上黑色节点数量相同，same black height

Attention

• Black height 计算时不算自己，算 NIL
• 所有有 key 的节点都是 internal node

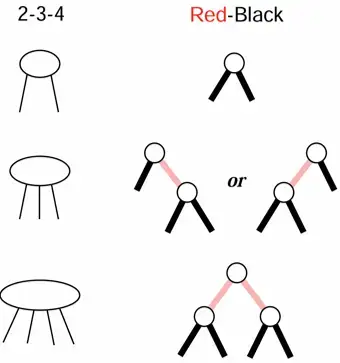
Red-Black Trees are just a way of representing 2-3-4 trees!

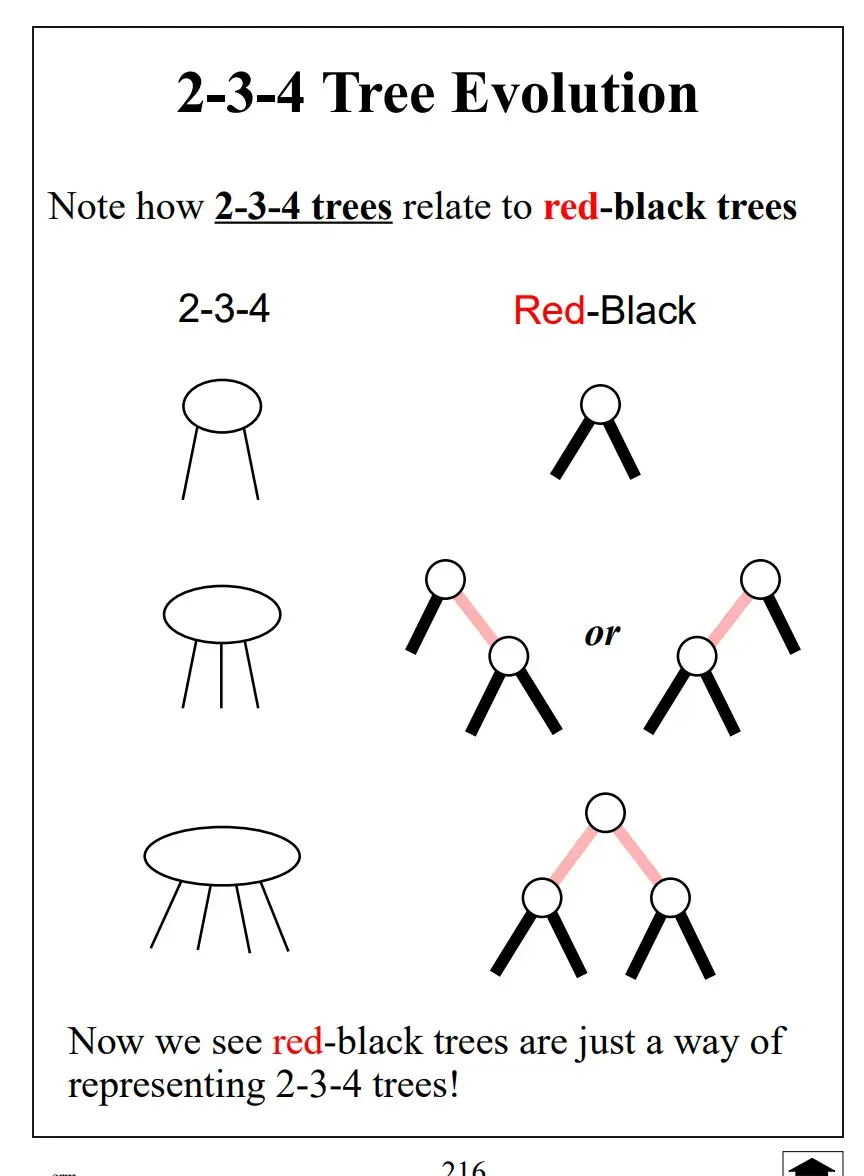
1.2 Black Height

\(Lemma\): A red-black tree with \(N\) internal nodes has height at most \(2\ln(N+1)\), 因此它是平衡树

\(Proof\): 数学归纳，即证 \(N\ge 2^{h/2}-1\)

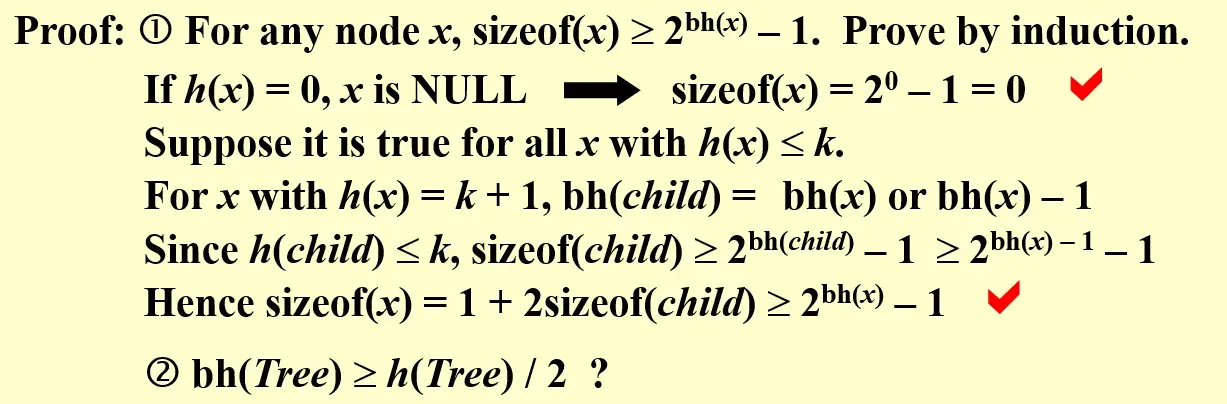
显而易见，没有连续的红色节点，所以 \(bh(x)\ge h(x)/2\)，证毕，原命题证毕

1.3 Insertion

1.3.1 Basic: Bottom-Up Insertion

Note

优先选择红色：不用改变 bh，有几率不需要做任何其他操作；但如果出现红色相邻，就要进行以下调整

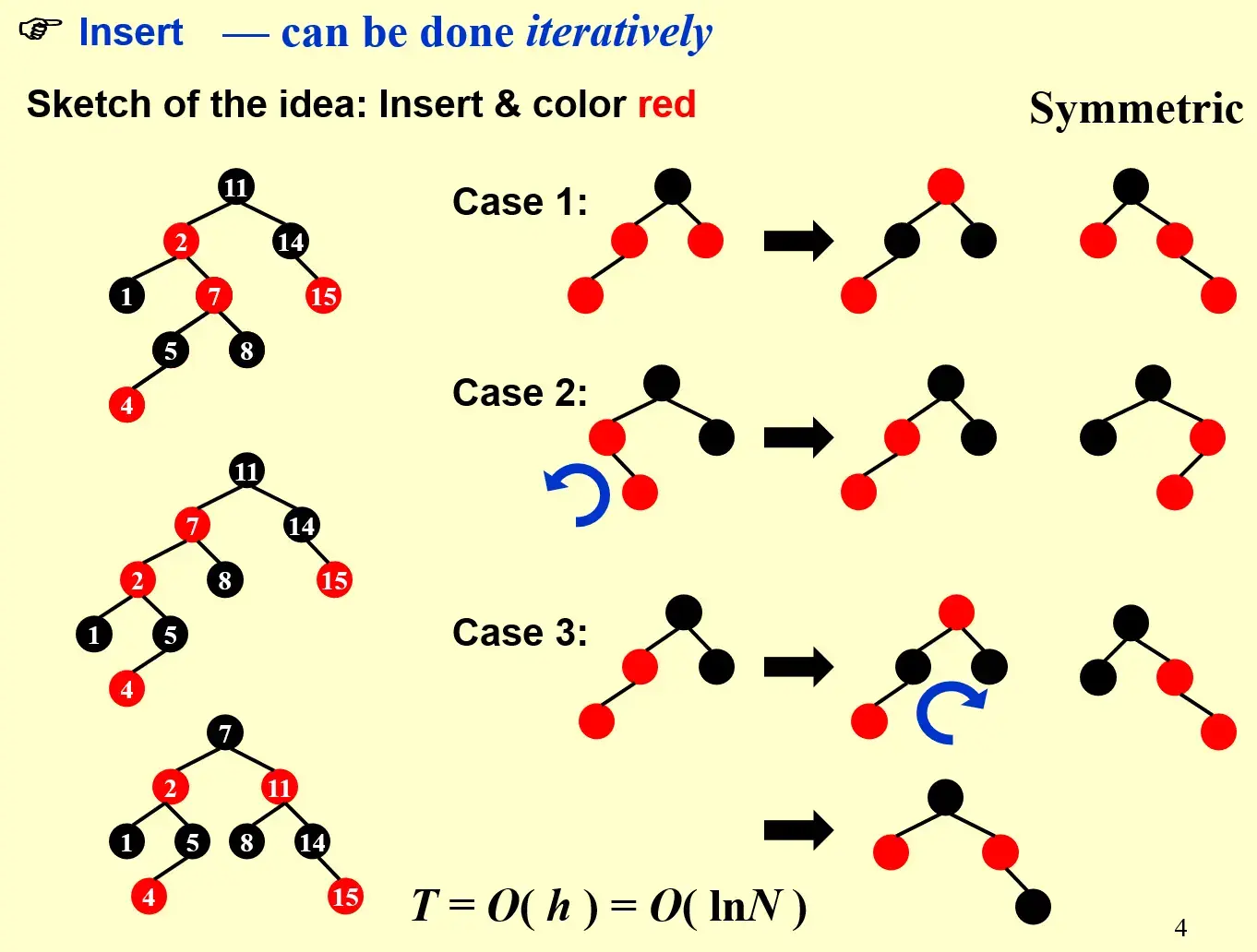
• Case 1: 解决局部问题，向上递归
• Case 2: 旋转，归纳为 Case 3
• Case 3: 更改颜色，为了修正 bh，需要旋转，Case 3 修正后就完成了，不需要向上传递

状态机

flowchart TD
    A[Case 1] -->|C| A
    C[Case3] -->|C&R| D(End)
    A -->|C| B[Case2]
    B -->|R| C
    A -->|C| C
    A -->|C| D

• 其中 C 为染色，R 为旋转
• 可以发现旋转操作最多也就 2 次

Dicussion

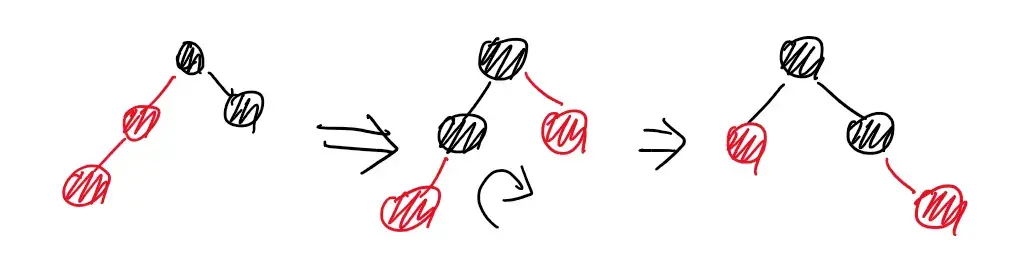为什么不行？

• 最右侧节点直接换红色可能导致出现红色节点连续
• P.right 子树的 bh 可能改变

1.3.2 Advanced: Top-Down Insertion

Question

Q1：为什么使用 Top-Down
A1：为了减少 rotation 的次数，不进行 percolate up
Q2：Top-Down 如何保证插入时最多只用 rotate 一次？
A2：在 search 的过程中进行操作，保证了插入节点的叔叔节点是黑色，直接来到 Case 3

1.3.2.1 Procedure

• Top-Down search 的过程中，如果发现一个节点 X 有两个红色孩子，那么将 X 染成红色，孩子染成黑色，注意此时 X 的父亲和叔叔不可能都是红色，否则它们将已经都被染成黑色
  • 若 X 的父亲是红色，其叔叔节点必为黑色，则进入 Case ⅔ 进行修正，不会产生递归
• 到了插入位置
  • 若父亲是红色，叔叔必为黑色，进入 Case ⅔，结束
  • 若父亲为黑色，结束

Example

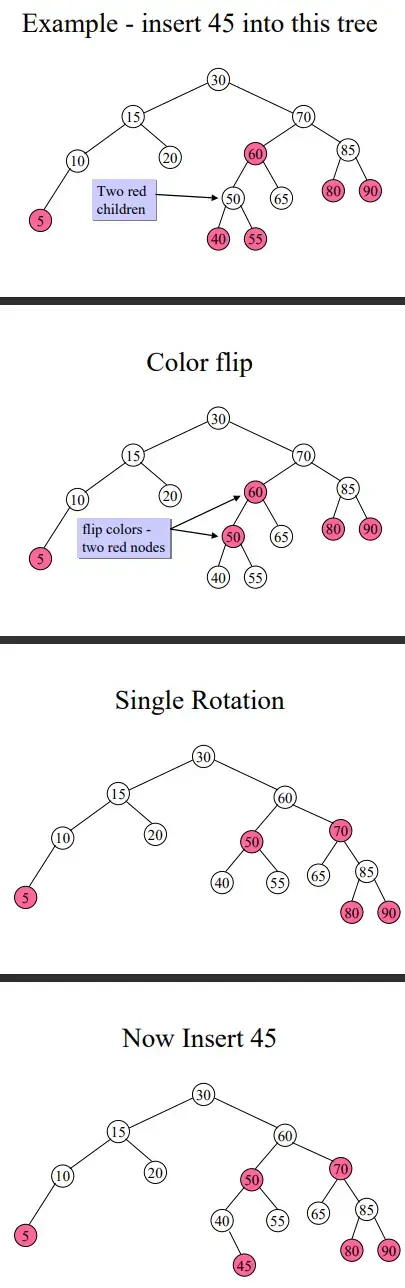
1.4 Deletion

1.4.1 Basic: Bottom-Up Deletion

1.4.1.1 Step 1. 查找并删除

1. Delete a leaf node: 这个节点就是 x，将父亲指向 NIL。如果这个节点是红色，进入 Step 2，否则，结束
2. Delete a degree 1 node:
   1. 先分析一下，如果这个节点是 degree 1，那么它的 bh = 1，它的孩子一定是红色，否则 bh 不相等，所以这个节点一定是黑色
   2. 用子节点替代待删除节点，并染成黑色，结束
3. Delete a degree 2 node: 将前驱（后继）的值 copy 过来并尝试删除前驱（后继），递归

找到 key 之后的流程图

flowchart TD
A[To delete leaf] -->|is red, delete|B{End}
A -->|is black, delete|D[Step 2: adjust black height]
C[To delete degree 1 node] -->|replace, recolor| B
E[To delete degree 2 node] -->|copy, recur| Z{Begin}
Z ---> |is leaf|A
Z --->|is degree 1| C
Z ---> |is degree 2|E

1.4.1.2 Step 2. 调整 Black Height

Target

x 是黑色叶子节点，让 x 所在的路径 bh+1 以保持平衡

1.4.1.2.1 Case 1 x 有红色邻居

Target

将邻居换成黑色，化归为其他 Case

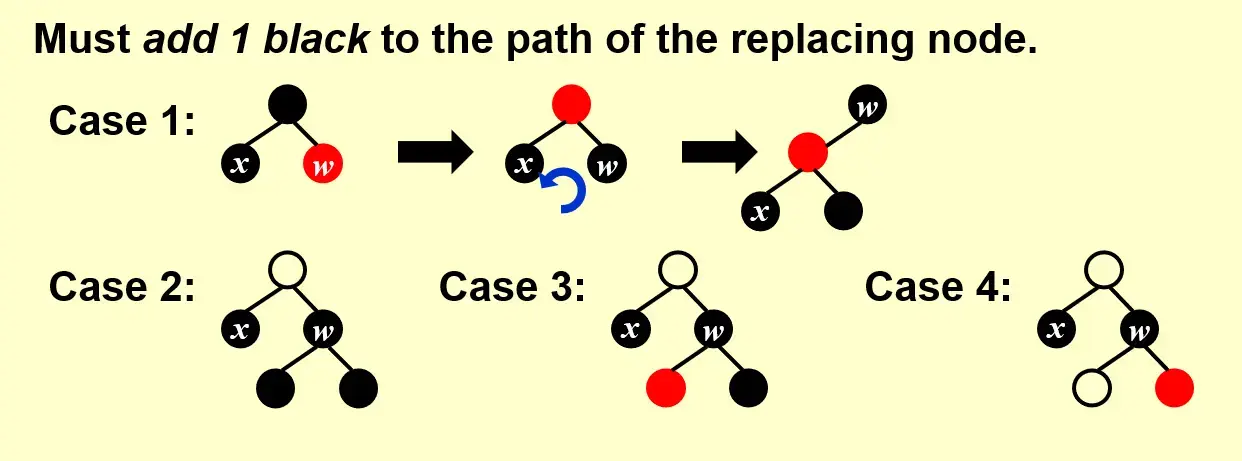
• 由于 w 是红色的，必有两个黑色孩子 考虑 NIL
• 进行染色，左侧 bh-1，右侧 bh 不变
• 进行旋转，左侧 bh+1，右侧 bh 不变
• 最终实现：
  1. 不改变左右的 bh
  2. 将 x 的邻居变成黑色，化归为其他 Case

1.4.1.2.2 Other cases x 有黑色邻居

Target

Add 1 black to the path of x, not to change others

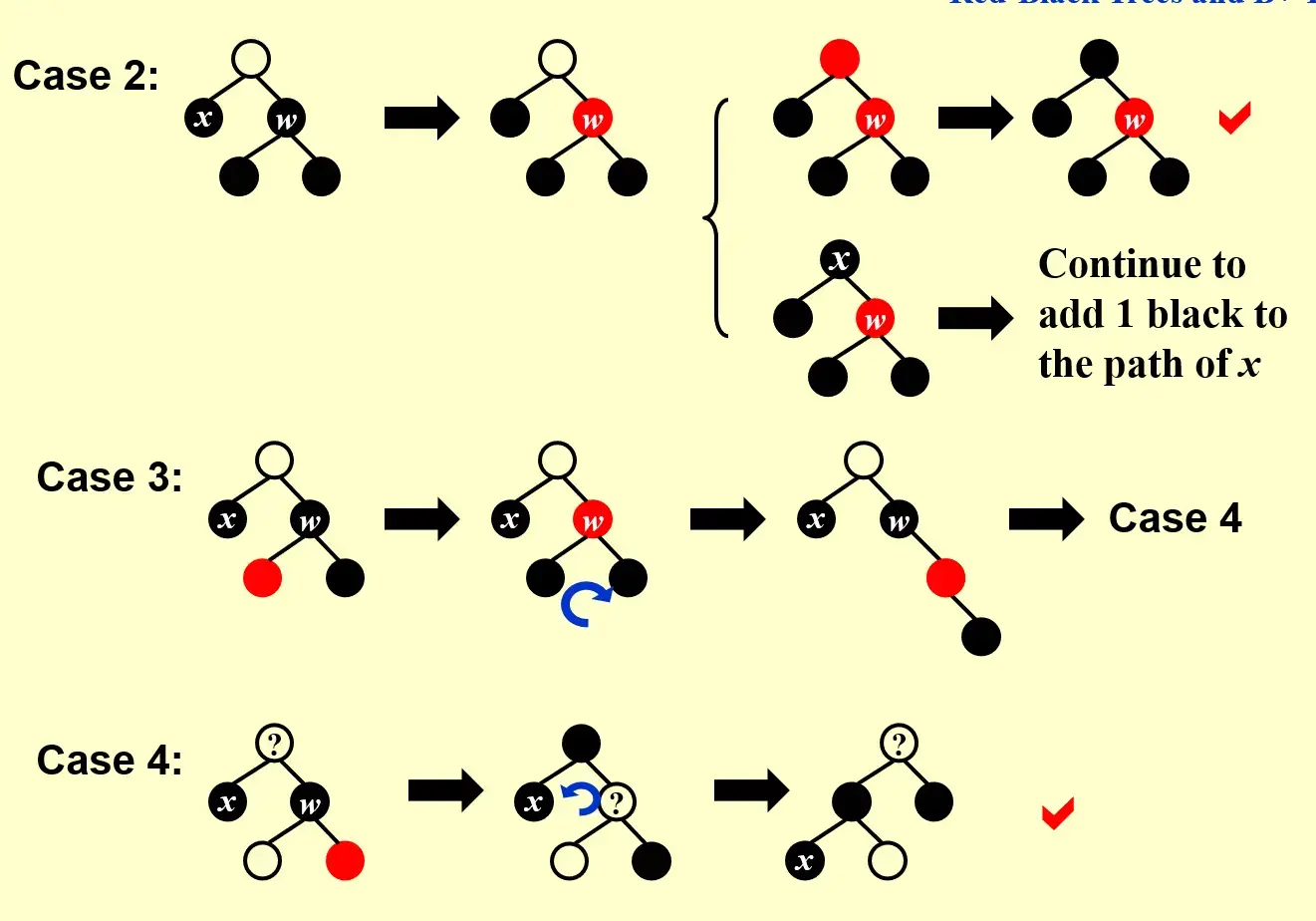
• 最多旋转次数为 3，Case 1 -> Case 2 -> Case 4 -> End

Example

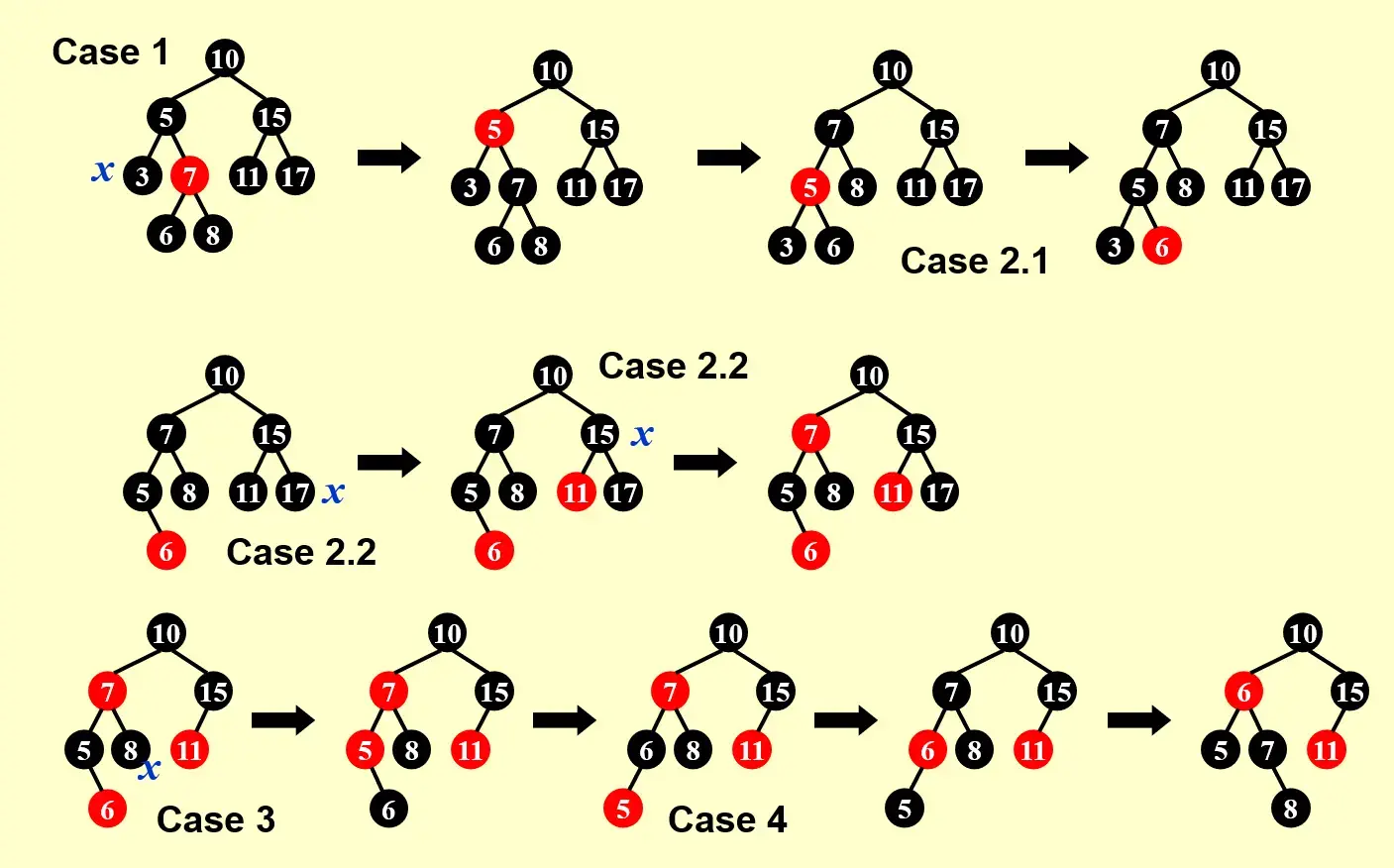
1.4.2 Advanced: Top-Down Deletion

Bug

并没有找到相关的资料？& 不知道和前面的 Bottom-Up 有什么具体区别？

1.5 Advantage

Number of rotations	AVL	RBT
Insertion	\(\le 2\)	\(\le 2\)
Deletion	\(O(\log N)\)	\(\le 3\)

2 B+ Trees

2.1 Definition

1. 根是叶子或有 \([2, M]\) 个孩子
2. 所有非叶子节点（除了根）都有 \([\lceil M/2\rceil, M]\) 个孩子
3. 所有叶子的深度相同

Important

• 所有数据都在叶子上
• 每个中间节点有 \(M\) 个 ptr，\(M-1\) 个 key value
• 每个叶子节点有 \(M\) 个 key 和 \(M\) 个 ptr，这里的 ptr 指向实际的数据结构而不是其他节点

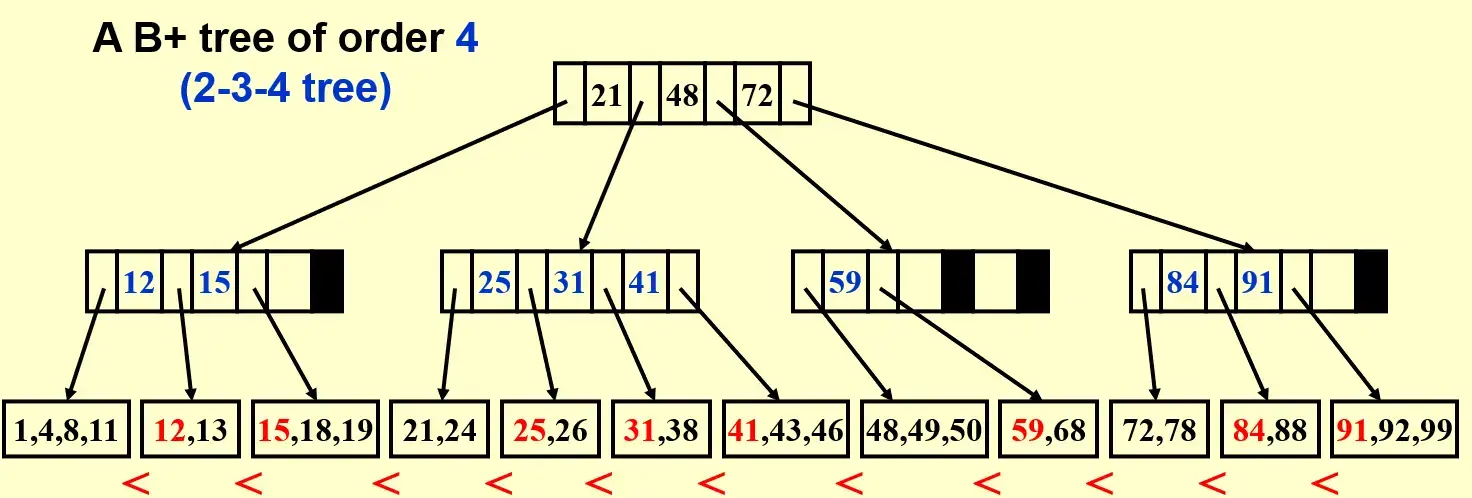
2.1.1 复杂度分析

考虑 \(M\) order B+ tree 有 N 个数据 - \(Depth(M, N)=O(\lceil \log_{\lceil M/2\rceil} N\rceil)\) - \(T_{find}=Depth(M, N) \times O(\log M)=O(\log N)\)

2.2 Insertion

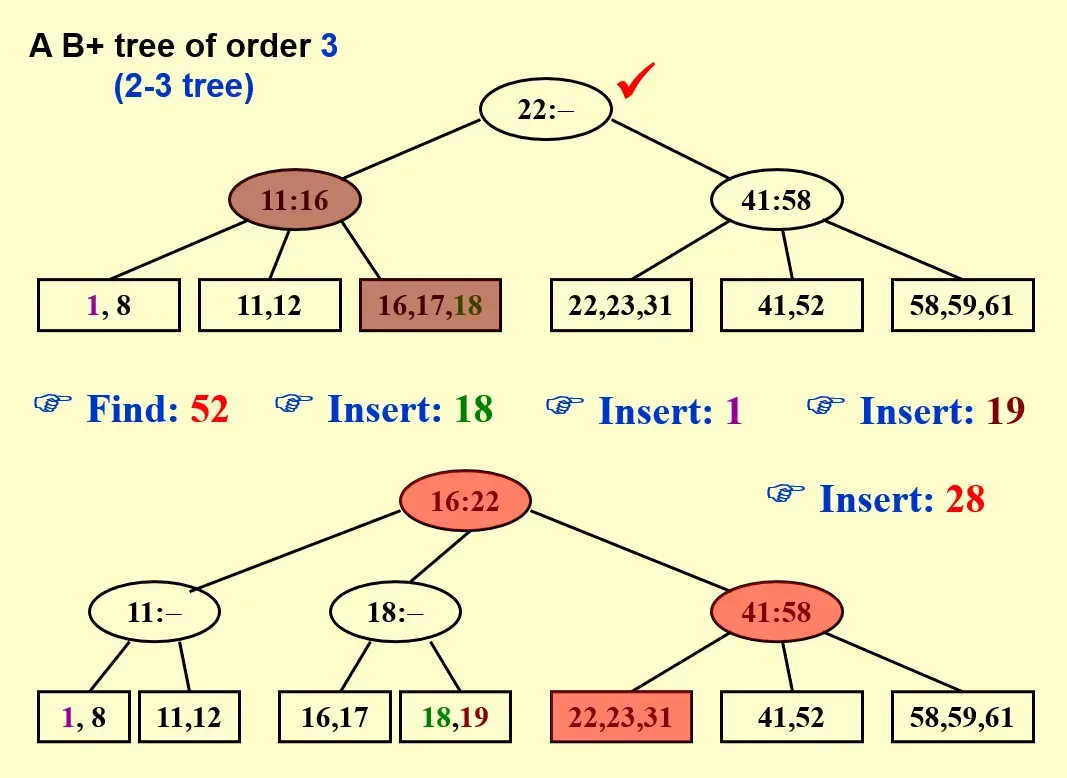
1. 找到要插入的位置，直接插入
2. 如果插入节点已满
   1. 可以查看同层的邻居还有没有位置，可以进行调整（如上图，其实可以匀一个位置出来，但这样的实现比较复杂）
   2. 进行分裂，并向上传递

Btree Insert ( ElementType X,  Btree T )
{
    Search from root to leaf for X and find the proper leaf node;
    Insert X;
    while ( this node has M+1 keys ) {
        split it into 2 nodes with \lceil (M+1)/2 \rceil and \lfloor (M+1)/2 \rfloor keys, respectively;
        if (this node is the root)
            create a new root with two children;
        check its parent;
    }
}

\[T_{insert}(M, N)=O((M/\log M)\log N)\]

Note

\(M\) 最好的选择是 3 或 4，但在数据库中经常选几千的

2.3 Deletion

类似 Insertion，当父节点只有一个孩子时，需要移除

A RB tree corresponds to a 2-3-4 tree

3 Questions

3.1 Q2

3.1.1 2-3 Tree 插入

When insert three keys into a non-empty 2-3 tree, and if the tree gains height when the first key is in, then it is possible that the 2-3 tree will gain more height after the insertions of the next two keys. (T/F)

Answer

F，因为如果树高增大的话，至少是从单个满的叶子节点（3keys）变成一根 2 叶子（4keys），这样完全可以容纳剩下的两个 key 而一定不会增加树高

3.1.2 Validity of a RBTree

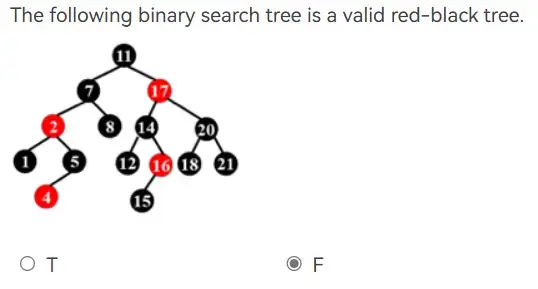
Answer

F，16 节点的 NIL 叶子黑高少一，总结为红色一度节点出现就非法

3.2 HW2

3.2.1 2-3 Tree 最多 key 数量

A 2-3 tree with 3 nonleaf nodes must have 18 keys at most. (T/F)

Answer

T
一定是一个根两个中间节点，所以 3*6=18

3.2.2 2-3 Tree 结构和插入详解

Insert 3, 1, 4, 5, 9, 2, 6, 8, 7, 0 into an initially empty 2-3 tree (with splitting). Which one of the following statements is FALSE?

• A. 7 and 8 are in the same node
• B. the parent of the node containing 5 has 3 children
• C. the first key stored in the root is 6
• D. there are 5 leaf nodes

Question: 2-3 树与 B+ 树的区别是什么，数据只在叶子节点还是在所有节点？

• 按照 2-3 Trees | (Search, Insert and Deletion) - GeeksforGeeks 所给的定义，2-3 树的每个节点都最多能有 2 keys, 3 pointer，并且数据不全在叶子上
• 所教的 2-3 树则更像是 B+ 树，所有数据全都在叶子节点上，中间节点最多 2 keys, 3 ptrs，叶子节点最多 3 keys

Answer

A¹

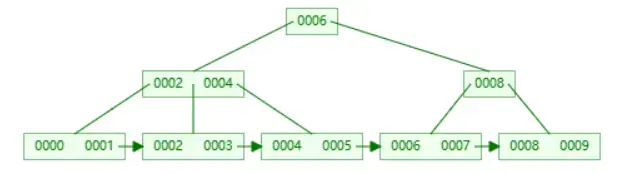
3.2.3 2-3 Tree 删除

After deleting 9 from the 2-3 tree given in the figure, which one of the following statements is FALSE?

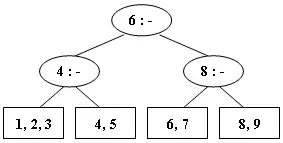
• A. the root is full
• B. the second key stored in the root is 6
• C. 6 and 8 are in the same node
• D. 6 and 5 are in the same node

Answer

D¹

3.2.4 Self-printable B+ Tree %% fold %%

• 实现 OEDER = 3 的 B+ 树插入和打印即可

3.3 Midterm Review

3.3.1 BPTree least 2-degree node

A B+ tree of order 3 with 21 numbers has at least __ nodes of degree 2.

Answer

0 这题不能_~贪心，~认为 2 度节点最少的情境下就是叶子节点最少；事实上，如果有 9 个叶子，就可以没有 2 度节点了 所以贪心方案应该是尽量构建全是 3 度节点的树

3.4 Midterm

3.4.1 RBTree Insert

After inserting { 1, 2, 3, 4, 5, 6, 7 } into an initially empty red-black tree, then the number of black nodes in the red-black tree is 4. (T/F)

Answer

T 建议再尝试一次

---

1. 图片来自 Homework - Jianjun Zhou's Notebook ↩↩

Comments