09 Greedy Algorithm

1 Introduction

1.1 Optimization Problems

• constraints 约束
• optimization function 目标函数
• feasible solution 可行解
• optimal solution 最优解

1.2 The Greedy Method

• 在每个阶段都按照一定的贪心方法做出局部最优选择，选择不可回溯、不可修改，每个选择都必须至少满足可行。
• 只能在 local optimal 局部最优 等于 global optimal 全局最优 的情况下得到最优解
• heuristics 近似：贪心法属于一种启发式算法，不一定能得到全局最优解，但是通常能够产生足够近似的可行解

2 Activity Selection Problem 活动选择问题

Question

给定活动的集合 \(S=\{a_{1},a_{2},a_{3},\dots,a_{n}\}\)，每个活动的持续时间为 \([s_{i},f_{i})\)，求一个房间最大能安排的活动数量

2.1 A DP Solution

每个贪心算法总是对应一个复杂度更高的 dp

• \(S_{ij}\) 表示从活动 \(a_i\) 到 \(a_j\) 的活动集合（不包括两端）

• \(c_{ij}\) 表示 \(S_{ij}\) 中最大安排活动数量，状态转移方程为 \(\(c_{ij}=\begin{cases}0 &\text{if }S_{ij}=\emptyset\\max_{{a_{k}\in S_{ij}}}\{c_{ik}+c_{kj}+1\}\quad &\text{if }S_{{ij}}\neq \emptyset\end{cases}\)\)

• \(T(N)=O(N^3)\)，这是因为有 \(i,j,k\) 三个变量的遍历

2.2 Greedy Solution

Select the interval which ends first but not causing overlapping. 关键思想在于尽早释放资源 \(T(N)=O(N \log N)\)

2.3 Correctness

• feasible: 保证不出现 overlapping，这显然成立
• optimal: 下面会给出证明

2.3.1 Proof of optimality

对于任意子问题，假设 \(A_{k}\) 是最优解的集合，\(a_{ef}\) 是 \(A_k\) 里最早完成的活动，\(a_m\) 是所有活动中最早完成的活动，那么

如果 \(a_m=a_{ef}\)，那么将会考虑两个相同的子问题，形成归纳；

否则，由于 \(a_{m}\leq a_{ef}\)，用 \(a_m\) 代替 \(a_{ef}\)，得到了和最优解一样好的 \(A_k'\)；

继续操作，总能得到和最优解一样好的 \(\hat{A_{k}}\)，其中所有元素都是子问题中最早结束的活动，这证明贪心结果和最优解等价。

交换参数法，通过构造不可能更差的解来证明贪心选择不可能比最优解差

2.4 Weighted Activity Selection 有权活动选择

• 简单来讲，只能用回 dp
• \(c_{1,j}\) 表示 \(a_1\) 到 \(a_j\) 里最好的安排，那么 \(c_{1,j}=\begin{cases}w_{1} &\text{if }j=1\\ \max\{c_{1,j-1},c_{1,k(j)}+w_{j}\}&\text{if }j>1\end{cases}\)

2.5 Interval Scheduling 区间调度问题

详见 6.2.3 Room Scheduling

3 Elements of the Greedy Strategy

1. 问题需要满足：做出一个选择，就留下一个子问题
2. 证明问题的最优解一定能够通过某种贪心过程得到
3. 证明最优子结构，即：
   当做出 greedy choice 后，余下的子问题具有这样的性质，子问题的最优解与先前的 greedy choice 合并后能够得到原始问题的最优解

Tip

Beneath every greedy algorithm, there is almost always a more cumbersome dynamic-programming solution.

4 Huffman Codes 霍夫曼编码

Huffman Coding 过于简单，可以参考离散的内容

void Huffman ( PriorityQueue  heap[ ],  int  C )
{   consider the C characters as C single node binary trees,
     and initialize them into a min heap;
     for ( i = 1; i < C; i++ ) { 
        create a new node;
        /* be greedy here */
        delete root from min heap and attach it to left_child of node;
        delete root from min heap and attach it to right_child of node;
        weight of node = sum of weights of its children;
        /* weight of a tree = sum of the frequencies of its leaves */
        insert node into min heap;
   }
}

• 算法
  • 构建优先队列，插入所有节点
  • 每次取权重最小的两个元素，作为一个新根的左右孩子，新根的权重为两个元素之和，将新根插入队列
  • 重复直到队列中只有一个元素
• \(T=O(C\log C)\)
• 所有的 character 都在叶子节点
• 每个 internal node 都是 2 degree 的，full tree
  • 区别于 complete tree 完全二叉树

4.1 Correctness

4.1.1 The greedy-choice property

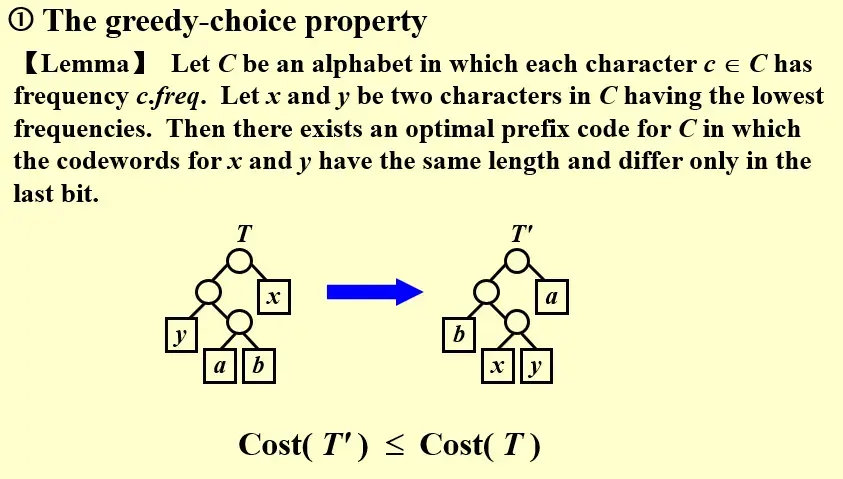
• 频率小的一定有更长的 prefix，频率最小的两个 prefix 长度相等且只有最后一个 bit 不同

4.1.2 The optimal substructure property

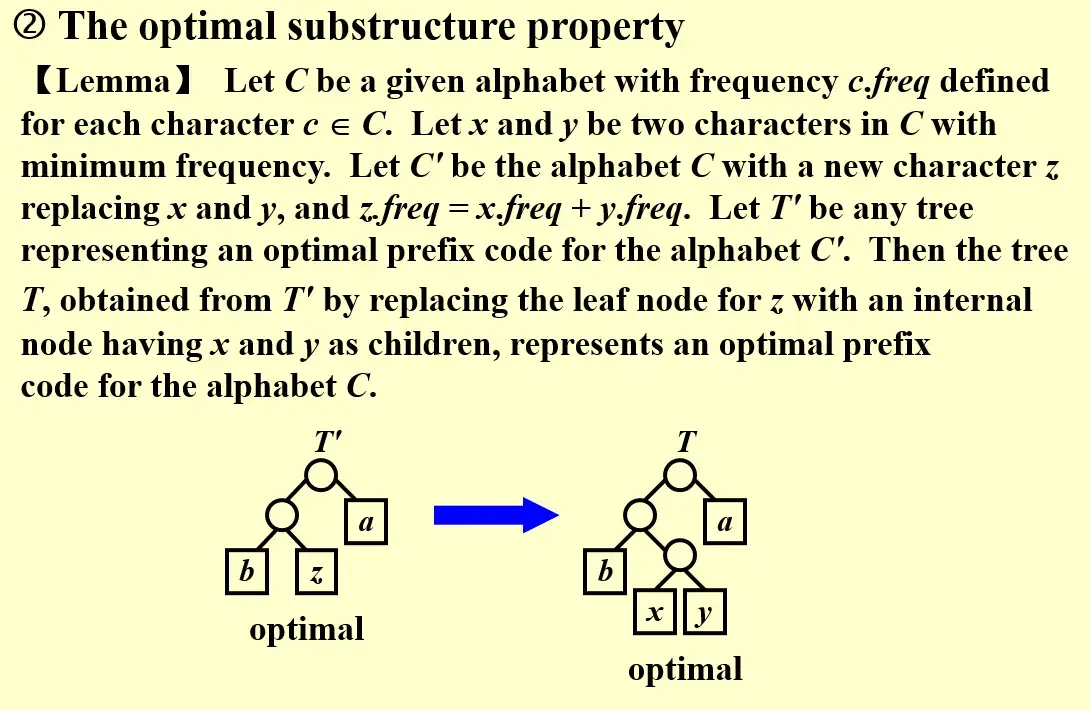
• \(x, y\) 节点在后面的解题过程中，与一个 \(z\) 节点等价，所以构成了最优子结构
• 可以使用反证法来证明这一点

5 Discussion

Question

Suppose that all the characters are sorted by their frequencies. Can you compute the Huffman code in \(O(n)\) time?

建立两个队列 \(Q_{1}, Q_{2}\)，其中 \(Q_{1}\) 就是排好序的 characters，\(Q_{2}\) 初始化为空。

每次考虑 \(Q_{1},Q_{2}\) 中的前两个共四个元素，将其中非空且最小的两个进行合并，enqueue 到 \(Q_{2}\)。

直到 \(Q_{1}\) 为空，\(Q_2\) 中只有一个元素时，这个元素就是结果。

证明：每次合并后得到的 trie 元素的总权重总是递增的，因此 \(Q_{2}\) 必然是增序的。

6 Questions

6.1 HW9

6.1.1 找零问题

Consider the problem of making change for n cents using the fewest number of coins. Assume that each coin's value is an integer. The coins of the lowest denomination（面额） is the cent.

(I) Suppose that the available coins are quarters (25 cents), dimes (10 cents), nickels (5 cents), and pennies (1 cent). The greedy algorithm always yields an optimal solution.

(II) Suppose that the available coins are in the denominations that are powers of c, that is, the denominations are \(c^0\), \(c^1\), ..., \(c^k\) for some integers \(c>1\) and \(k\geq1\). The greedy algorithm always yields an optimal solution.

(III) Given any set of k different coin denominations which includes a penny (1 cent) so that there is a solution for every value of n, greedy algorithm always yields an optimal solution.

Which of the them are correct?

Answer

只有 III 错

• 关键问题是，如果剩余的空缺刚好能用两个中等面值填上，但如果放了最大面值，可能还需要放很多个最小面值，远远超过两个，这样就不是最优解，所以 III 肯定错
• II 是 \(c\) 进制唯一表示，肯定对
• 现在考虑解决这个关键问题，假设面值递增序列为 \(w_{i}\)，满足贪心要求的面值满足以下其一
  • \(w_{i+1}=k*w_{i}\)，即 \(w_{i+1}\) 是 \(w_i\) 的整数倍
  • 若 \(w_{i+1}\) 不是 \(w_i\) 整数倍，那么存在一个 \(k_{i}\)，使得 \((k_{i}-1)w_{i}<w_{i+1}\)，且 \(k_{i}w_{i}>w_{i+1}\)；若 \(k_{i}w_{i}=w_{i+1}+k_{i-1}w_{i-1}+k_{i-1}w_{{i-2}}+\dots+k_{0}w_{0}\)，必须满足 \(k_{i}\geq 1+k_{i-1}+k_{i-2}+\dots+k_{0}\)

6.1.2 Fill or Not to Fill %% fold %%

Question

With highways available, driving a car from Hangzhou to any other city is easy. But since the tank capacity of a car is limited, we have to find gas stations on the way from time to time. Different gas station may give different price. You are asked to carefully design the cheapest route to go.

Input Specification:

Each input file contains one test case. For each case, the first line contains 4 positive numbers: \(C_{max}\)​ (≤ 100), the maximum capacity of the tank; \(D\) (≤30000), the distance between Hangzhou and the destination city; \(D_{avg}\)​ (≤20), the average distance per unit gas that the car can run; and \(N\) (≤ 500), the total number of gas stations. Then \(N\) lines follow, each contains a pair of non-negative numbers: \(P_{i}\)​, the unit gas price, and \(D_i\)​ (≤\(D\)), the distance between this station and Hangzhou, for \(i=1,\dots,N\). All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the cheapest price in a line, accurate up to 2 decimal places. It is assumed that the tank is empty at the beginning. If it is impossible to reach the destination, print The maximum travel distance = X where X is the maximum possible distance the car can run, accurate up to 2 decimal places.

Sample Input 1:

50 1300 12 8
6.00 1250
7.00 600
7.00 150
7.10 0
7.20 200
7.50 400
7.30 1000
6.85 300

Sample Output 1:

749.17

Sample Input 2:

50 1300 12 2
7.10 0
7.00 600

Sample Output 2:

The maximum travel distance = 1200.00

assign the destination to be station N with price 0.0

if is not at the 1st station:
    print maximum dist = 0.0
    exit

while i < N:
    // assume now at station i
    if there is not station accessible in the next run:
        maximum dist = current dist + max run
        print maximum dist
        exit
    else:
        int next
        for station j in accessible stations:
            if station j is the cheapest among accessible stations:
                next = j
            if station j is cheaper than station i:
                break

        if next is cheaper than i:
            try to get just enough fuel to go to next
            i = next
        else:
            fill the tank
            i = next

if i == N:
    print total cost

6.2 Ex9

6.2.1 Vertex Cover Problem

To solve the vertex cover problem, there is a greedy algorithm that collects the vertex with the highest degree (i.e., the one covering the largest number of edges) and remove it from the graph at each stage. This greedy algorithm achieves an approximation ratio of 2. (T/F)

Answer

F 顶点覆盖问题是从 \(G\) 中取尽量少的顶点组成集合 \(C\)，使得每一条边都和 \(C\) 中至少一个顶点相连；这是一个 NP-C 问题。 一种近似算法如下：

C = null
E = G.E
while E != null:
    let (u, v) be an arbitraty edge of E
    C = C union {u, v}
    remove from E edge (u, v) and every edge incident on either u or v
return C

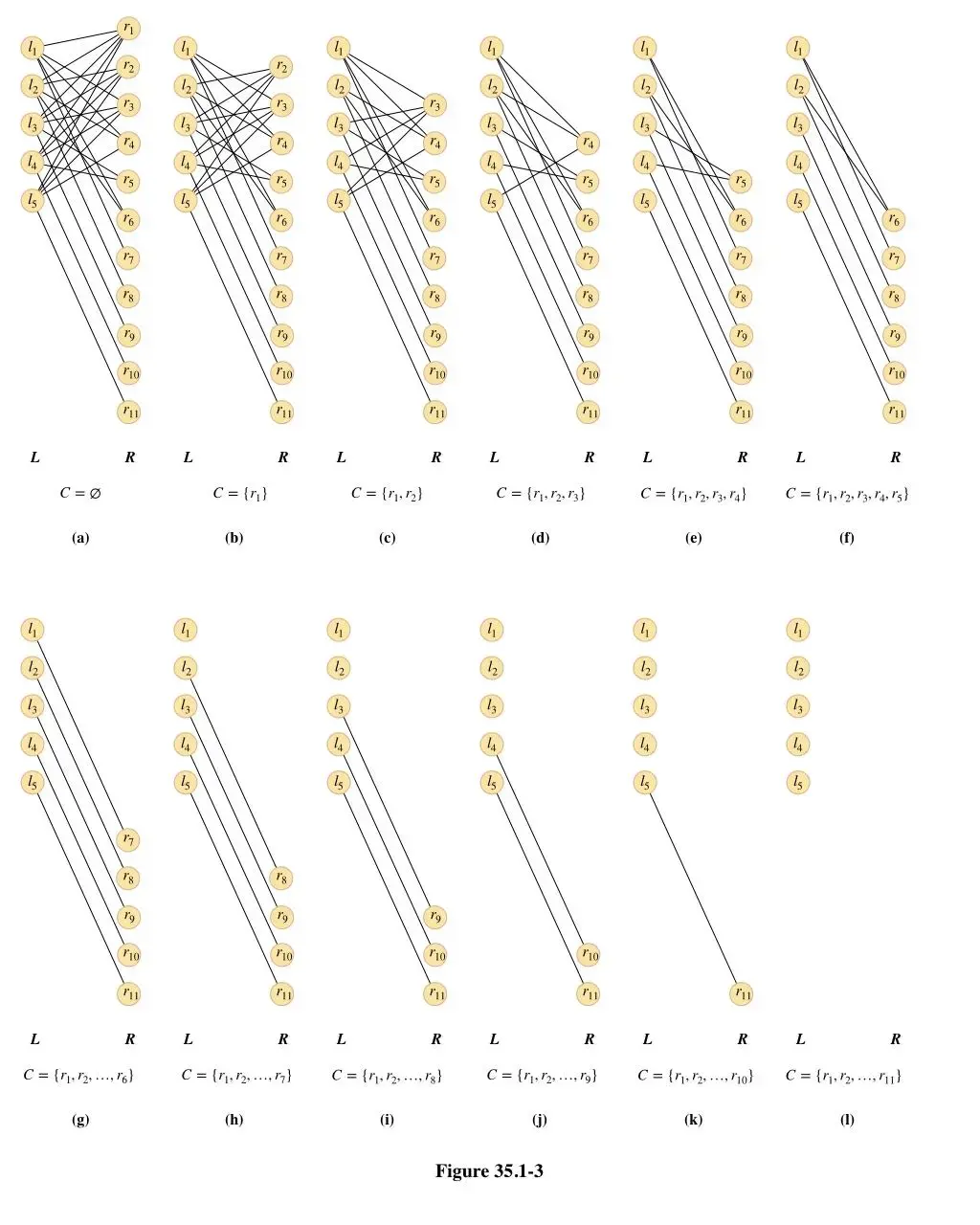如果使用题目的算法（启发式算法），其解的近似比是大于 2 的，可以举出这样一个例子 ¹： 此时，最优解是左边的 5 个顶点，但是算法会找到右边的所有 11 个顶点，于是近似比 \(\geq 11/5\)

6.2.2 Binary Tree and Prefix Code

A binary tree that is not full cannot correspond to an optimal prefix code. (T/F)

Answer

T 注意区分 full 和 complete 的概念，满树没有一度节点

6.2.3 Room Scheduling

In Activity Selection Problem, we are given a set of activities \(S=\{a_1 ​,a_2​, \dots, a_{n}\}\) that wish to use a resource (e.g. a room). Each \(a_{i}​\) takes place during a time interval \([si​,fi​)\).

Let us consider the following problem: given the set of activities \(S\), we must schedule them all using the minimum number of rooms.

Greedy1: Use the optimal algorithm for the Activity Selection Problem to find the max number of activities that can be scheduled in one room. Delete and repeat on the rest, until no activities left.

Greedy2:

• Sort activities by start time. Open room \(1\) for \(a_1\)​.
• for \(i=2\) to \(n\) if \(a_i\)​ can fit in any open room, schedule it in that room; otherwise open a new room for \(a_i\)​.

Are they optimal methods?

Answer

Greedy1 is not, while Greedy2 is

对于 Greedy1，可以举出一个反例，如 (1,4),(2,5),(6,7),(4,8) ²

对于Greedy2，先给出一个最优解：关键在于最大化利用已经安排了活动的教室，所以不能随意安排进能用的教室；要对已经安排了活动的教室的下一个释放时间放到 minHeap 中，对于每个活动，先与这个最早的释放时间比较，如果大于则安排到那个教室并重新插入堆；如果小于则必须开辟新的教室，伪代码如下 ²：

sort activities by starting time in ascending order
H = null  // minHeap of room release time 
create room for course[0], calculate release time, insert to H

for activity 1 to N:
    if activity.start > H.top:
        room = H.pop
        assign activity to room
        recalculate release time insert room to H
    else:
        create a new room, assign activity, calculate release time, insert to H

可以发现，Greedy2 和上述最优解其实是等价的，如果到这个活动开始的时候有很多房间都空了，从这个时间点之后这些房间如何安排其实是等价的，可以相互交换，随机安排也是最优解

6.3 Q10

6.3.1 Proof of greedy algo

To prove the correctness of a greedy algorithm, we must prove that an optimal solution to the original problem always makes the greedy choice, so that the greedy choice is always safe.

Answer

F，证明的要点有很多

1. 优化问题能够经过 choice 变成子问题 Cast the optimization problem as one in which we make a choice and are left with one subproblem to solve.

2. 证明一定存在某种最优解，能通过某种贪心过程得到 Prove that there is always an optimal solution to the original problem that makes the greedy choice, so that the greedy choice is always safe.

3. 证明最优子结构 Demonstrate optimal substructure by showing that, having make the greedy choice, what remains is a subproblem with the property that if we combine an optimal solution to the subproblem with the greedy choice we have made, we arrive at an optimal solution to the original problem.

---

1. 来自 算法导论（第四版）第三十五章：近似算法　第一节：顶点覆盖问题 - 知乎 ↩

2. 参考 算法导论16章贪心算法习题活动教室分配问题（区间图着色问题）分析详解与代码实现-CSDN博客 ↩↩

Comments