15 External Sorting
1 Introduction#
Quicksort on a disk is slow because of random access. Use Merge-sort to optimize.
1.1 Terms#
- simplification
- 将数据存在 tape 上,只能顺序访问
- 至少有 3 个 tape drives
- run: 归并子序列
- pass: 初始创建归并段或者归并段大小增加一倍称为一个 pass
- \(\text{\#passes}=1+\lceil \log_{2} (N/M) \rceil\)
- 有序归并段长度指数增长,所以有 \(\lceil \log_{2}(N/M) \rceil\)
- 另外还有第一次排序

- efficiency concerns
- #passes
- parallelism
- block
2 \(k\)-way Merge#
\(k\)-way,表示一次合并有 \(k\) 个指针
- 用 minheap 处理每个 way 的当前最小元素,每次写入最小的元素
- 至少需要 \(2k\) tape,同一时刻有 \(k\) 条读、\(k\) 条写
2.1 Less tapes: Polyphase merge#
- 2-way 3 tapes
- 如果每次二等分操作,\(\text{\#passes}=1+2\log_{2}\lceil N/M \rceil\),因为可能出现需要一直
- 如果不均匀分割,最优方法是近似成 fibonacci,\(\text{\#passes}=1+\log_{1.618}\lceil N/M \rceil\)
- \(k\)-way \(k+1\) tapes
- \(k\) 阶 fibonacci 序列:\(F_{N}=\sum_{i=N-k}^{N-1}F_{i}\),而且 \(F_{k-1}=1, F_{i}=0\text{ for } i <k-1\)
2.2 Buffers#
- internal memory 分成 input buffer 和 output buffer,最小划分单位是 block
- 每当一个 output buffer 写满,则输出到 disk
- 双缓冲
- 给 output buffer 分配一个备份,output 不会打断排序
- 给 input buffer 也分配一个备份,input 不会打断排序
- 所以一共 \(k\)-way 需要 \(2k+2\) 个 buffer
2.3 Longer run: Replacement selection#
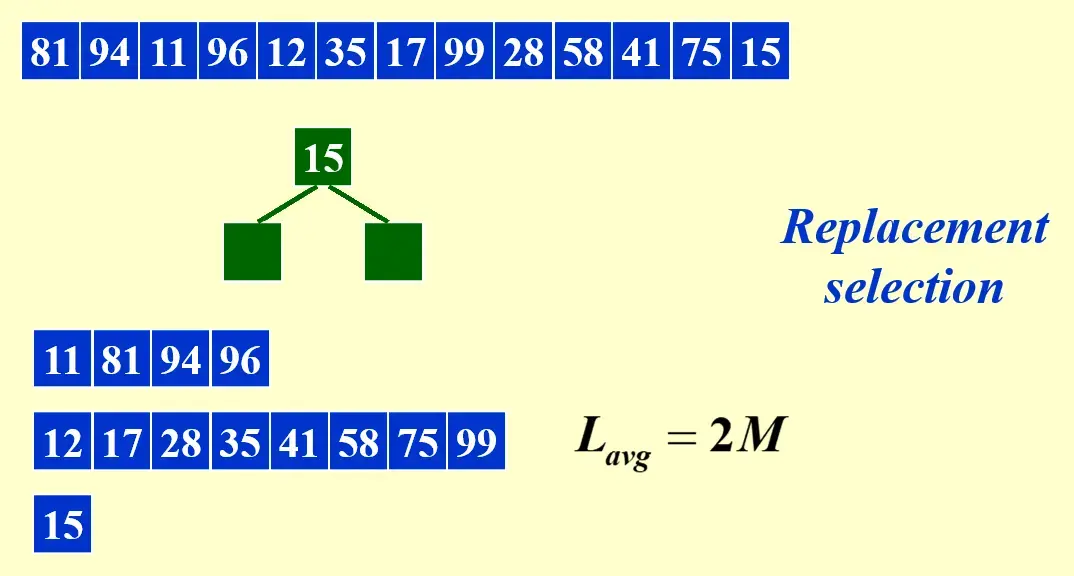
输出时,在 heap 中继续放入下一个数,直到这个数比上一个输出的小,标记一个 cut
期望 run 长度为 \(2M\)
2.3.1 Minimize merge time#
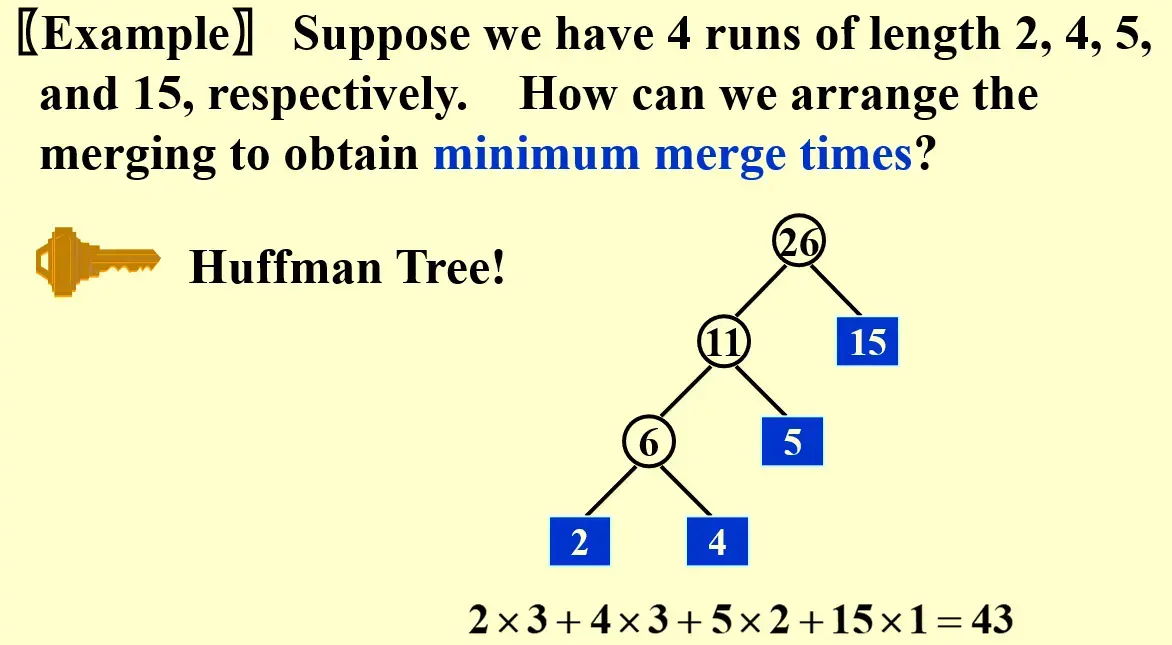
永远只合并最小的,所以形成 Huffman Tree 的结构
3 Discussion#
3.1 Tournament Trees#
Question
Tournament tree is a complete binary tree with n external nodes and n−1 internal nodes. The external nodes represent the players and internal nodes represent the winner/loser of the match between the two players.
There are mainly two type of tournament tree:
- Winner tree: each node represents the winner. The final winner is represented by the root.
- Loser tree: The loser of the match is stored in internal nodes of the tree. But the overall winner of the tournament is stored at tree[0].
Tournament tree may be used in k-way merges.
What are the differences between winner and loser trees? Which one would you prefer for k-way merge? Why?
The winner tree stores the winner in internal nodes, while loser tree stores the loser in internal nodes. The loser tree is better for k-way merge. When the element on a tape is updated, all the necessary elements to compare is stored in its way to path, thus eliminating unnecessary comparisons.
3.2 The expected run length#
Question
Suppose that the internal memory can handle \(M = 7\) records at a time. Given the input sequence { 19, 12, 25, 31, 56, 21, 40, 16, 29, 14, 35, 23 }. What are the runs generated by the replacement selection?
What is the best case? How about the worst case?
Why is the expected length of a run generated by replacement selection \(2M\) (where \(M\) is the internal memory size)?
{12, 16, 19, 21, 25, 29, 31, 35, 40, 56}, {14, 23}
- Worst case: the input sequence is sorted in reversed order, all runs have the length of \(M\).
- Best case: the input sequence is already sorted, only 1 run is generated, and the sorting is done.
For a memory with the size off \(M\) records, the expected times that any record in the memory can be replaced in this method is \(1/0.5=2\). Thus, the expected length of a run is \(2M\).
4 Questions#
4.1 HW15#
4.1.1 One tape drive#
If only one tape drive is available to perform the external sorting, then the tape access time for any algorithm will be \(Ω(N^2)\).
Answer
T, 寻道时间从 \(\Omega (1)\) 为 \(\Omega (N)\)
4.2 Parallel cycles#
Suppose we have the internal memory that can handle 12 numbers at a time, and the following two runs on the tapes:
Run 1: 1, 3, 5, 7, 8, 9, 10, 12
Run 2: 2, 4, 6, 15, 20, 25, 30, 32
Use 2-way merge with 4 input buffers and 2 output buffers for parallel operations. Which of the following three operations are NOT done in parallel?
A. 1 and 2 are written onto the third tape; 3 and 4 are merged into an output buffer; 6 and 15 are read into an input buffer
B. 3 and 4 are written onto the third tape; 5 and 6 are merged into an output buffer; 8 and 9 are read into an input buffer
C. 5 and 6 are written onto the third tape; 7 and 8 are merged into an output buffer; 20 and 25 are read into an input buffer
D. 7 and 8 are written onto the third tape; 9 and 15 are merged into an output buffer; 10 and 12 are read into an input buffer
Answer
D
因为这个时候,第一个 way 原有的 (_, 7), (8, 9) 中 (7, 8) 被 merge 了,但是仍然要等待 (10, 12) 在下一个周期中加载,再下一个周期才能继续 merge (9, 10)
4.3 Ex15#
4.3.1 To sort \(N\) numbers by...#

Answer
A 引入败者树后,比较和归并的次数与 \(k\) 无关!