07 Divide and Conquer

1 Intro

• The maximum subsequence sum
  • \(T(N)=2T(N/2)+O(N)\)
  • \(T(N)=O(N\log N)\)
• Tree traversals
  • \(T(N)=2T(N/2)\)
  • \(T(N)=O(N)\)
• Mergesort and quicksort
  • \(T(N)=2T(N/2)+O(N)\)
  • \(T(N)=O(N\log N)\)

出发点：递推公式

\[T(N)=aT(\frac{N}{b})+f(N)\]

1.1 Example: Closest Points Problem

Question

一个平面上有 \(N\) 个点，找到距离最近的一对点

• Divide
  • 找到一条直线，平分所有点 re
  • 变成两个子问题
• Conquer
  • 若子问题中找到的最小距离为 \(\delta\)，在分割直线左右两侧 \(\pm \delta\) 范围内查找是否有更小的距离
  • problem: 如何减小合并的复杂度？

Solution

按照一个方向坐标大小进行排序，然后顺序遍历，如果相邻的两个节点在这个方向上距离小于 \(\delta\)，才考虑它们之间的距离，并更新点对和 \(\delta\)
这样就是 \(O(N)\)

\(T(N)=2T(N/2)+O(N)=O(N\log N)\)

优化前后时间复杂度推导和对比

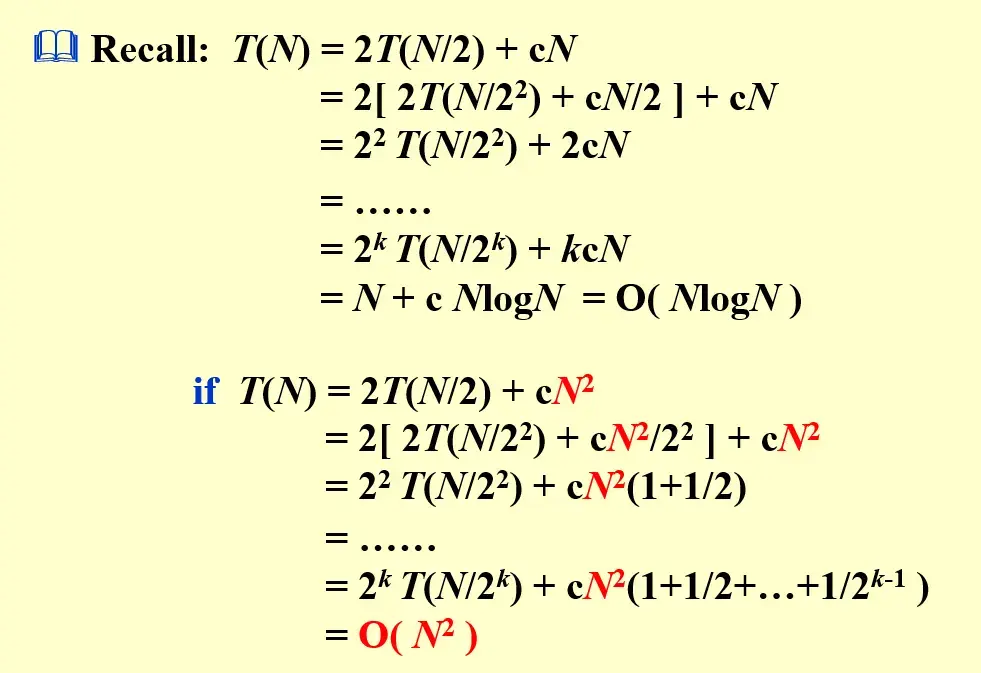
2 Solving Recurrences

• Three methods for solving recurrences
  • Substitution method 代换法
  • Recursion-tree method 递归树法
  • Master method 主方法
• Details to be ignored
  • if \(N/b\) is int or not
  • always assume \(T(n)=\Theta(1)\) for small \(n\)

2.1 Substitution Method

进行猜测，然后使用归纳法证明，方便用于验证

Example

\[T(N)=2T\left( \left\lfloor \frac{N}{2} \right\rfloor \right)+N\]

假设对于所有 \(m<N\) 都成立，那么当 \(m=\lfloor N/2 \rfloor\) 时也成立，即存在常数 \(c\geq 1\) 使得：

\[T(\lfloor N/2 \rfloor)\leq c \lfloor N/2 \rfloor \log \lfloor N/2 \rfloor\]

那么：

\[ \begin{align} T(N)&=2T(\lfloor N/2 \rfloor )+N \\ &\leq 2c\lfloor N/2 \rfloor +N \\ &\leq cN(\log N-\log 2)+N \\ &\leq cN\log N \end{align} \]

由此完成归纳，证毕。

Attention

可以选择足够大的常数 \(c\)，使得假设对于 \(N=1\) 等较小的 case 也一定成立

Exact form

放缩的时候必须确保常数不会变大

2.2 Recursion-tree Method

Example

\[T(N)=3T(N/4)+\Theta(N^2)\]

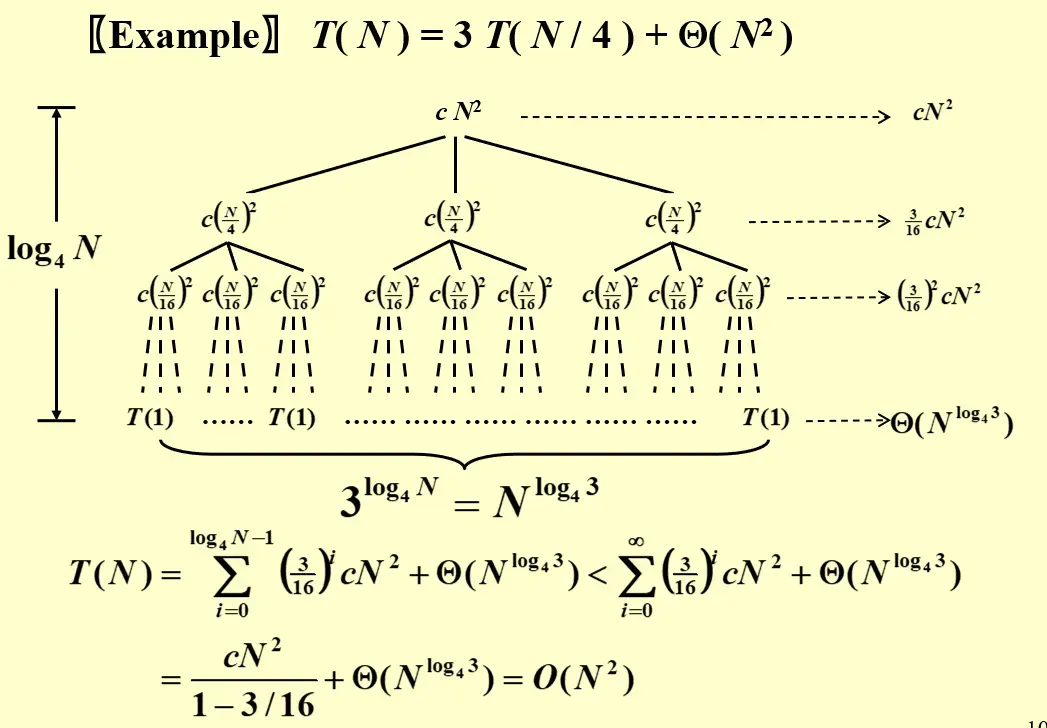
不一定适用于所有情况！

这里展开之后是斜树，可以计算但比较麻烦

比较新颖的一道题

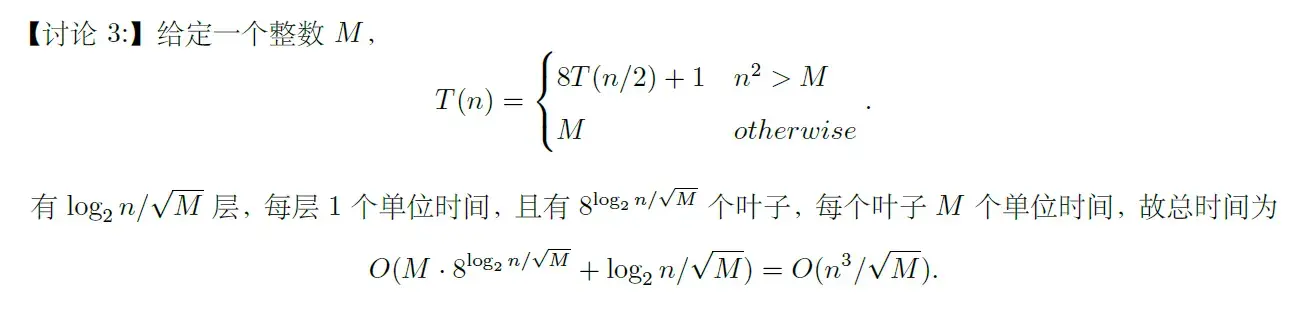
• 核心思路是一样的，找出叶子的数量和分叉的数量，计算和比较开销
• 这里不是每层开销不是一个单位时间，而是本层的节点数量，所以答案应该是 \(O(M \cdot 8^{\log_{2}n/\sqrt{ M }}+\frac{8^{\log_{2}n/\sqrt{ M }}-1}{8-1})=O(M \cdot 8^{\log_{2}n/\sqrt{ M }})=O(n^3/\sqrt{ M })\)

2.3 Master method

2.3.1 form 1

对于递推式 \(T(N)=aT(N/b)+f(N)\)，有：

1. 如果 \(f(N)=O(N^{\log_{b}a-\epsilon}\))，即 \(f(N)\) 的阶低于 \(\log_{b}a\)，那么 divide 是主要开销，\(T(N)=\Theta(N^{\log_{b}a})\)
2. 如果 \(f(N)=\Theta(N^{\log_{b}a})\)，即二者开销同阶，\(T(N)=\Theta(N^{\log_{b}a}\log N)\)
3. 如果 \(f(N)=\Omega(N^{\log_{b}a+\epsilon})\)，即 \(f(N)\) 的阶高于 \(log_b a\)，且 \(af(N/b)<cf(N)\) (regularity condition)，那么 conquer 是主要开销，\(T(N)=\Theta(F(N))\)

Attention

无法覆盖所有条件，例如 \(T(N)=2T(N/2)+N\log N\) 不满足任何一种条件，但是可以使用 2.3.4 form 3 来解决

Regularity Condition 的作用

Polynomially smaller

Polynomially smaller 是指一个函数与另一个函数相比，在增长速率上相差一个多项式级别。

具体来说，如果有两个函数 \( f(n) \) 和 \( g(n) \)，我们说 \( f(n) \) polynomially smaller（多项式级别小）于 \( g(n) \)，意味着存在某个多项式函数 \( n^k \)，使得

\[f(n) = O(\frac{g(n)}{n^{k}})\]

换句话说，\( f(n) \) 的增长速率比 \( g(n) \) 慢，并且相差一个多项式因子 \( n^k \)，其中 \( k \) 是一个常数。

举例

1. \( f(n) = n \) 和 \( g(n) = n^2 \)： 在这种情况下，\( f(n) \) 是 \( g(n) \) 的多项式级别小，因为 \( n = O\left(\frac{n^2}{n}\right) \)，这里 \( k = 1 \)，所以 \( n \) 是 \( n^2 \) 的多项式级别小。

2. \( f(n) = n \) 和 \( g(n) = n^3 \)： 这里 \( f(n) \) 也是 \( g(n) \) 的多项式级别小，因为 \( n = O\left(\frac{n^3}{n^2}\right) \)，这里 \( k = 2 \)，所以 \( n \) 是 \( n^3 \) 的多项式级别小。

为什么多项式级别小很重要？

在算法分析中，特别是递归分析或分治算法的分析中，多项式级别小的概念经常用来比较递归关系中不同部分的增长速率。比如：

• 在 Master Theorem 中，当你分析递归关系时，会比较子问题的数量（即递归部分）与额外的工作量（即合并部分）。如果合并部分（比如 \( f(n) \)）在某一层比递归部分（比如 \( aT(n/b) \)）要小得多，那么可以认为这个合并部分是 多项式级别小，递归部分占主导地位。
• 反之，如果 \( f(n) \) 增长得与递归部分差不多或者更快，那么合并部分会成为主要开销，这时就会有不同的时间复杂度分析。

总结

"Polynomially smaller" 就是指在增长速度上，两个函数相差一个多项式的级别。这个概念在分析算法和递归关系时经常出现，帮助我们判断哪些部分在整体复杂度中占主导地位，哪些部分可以忽略掉。

2.3.2 Prove by Recursion-tree

2.3.3 form 2

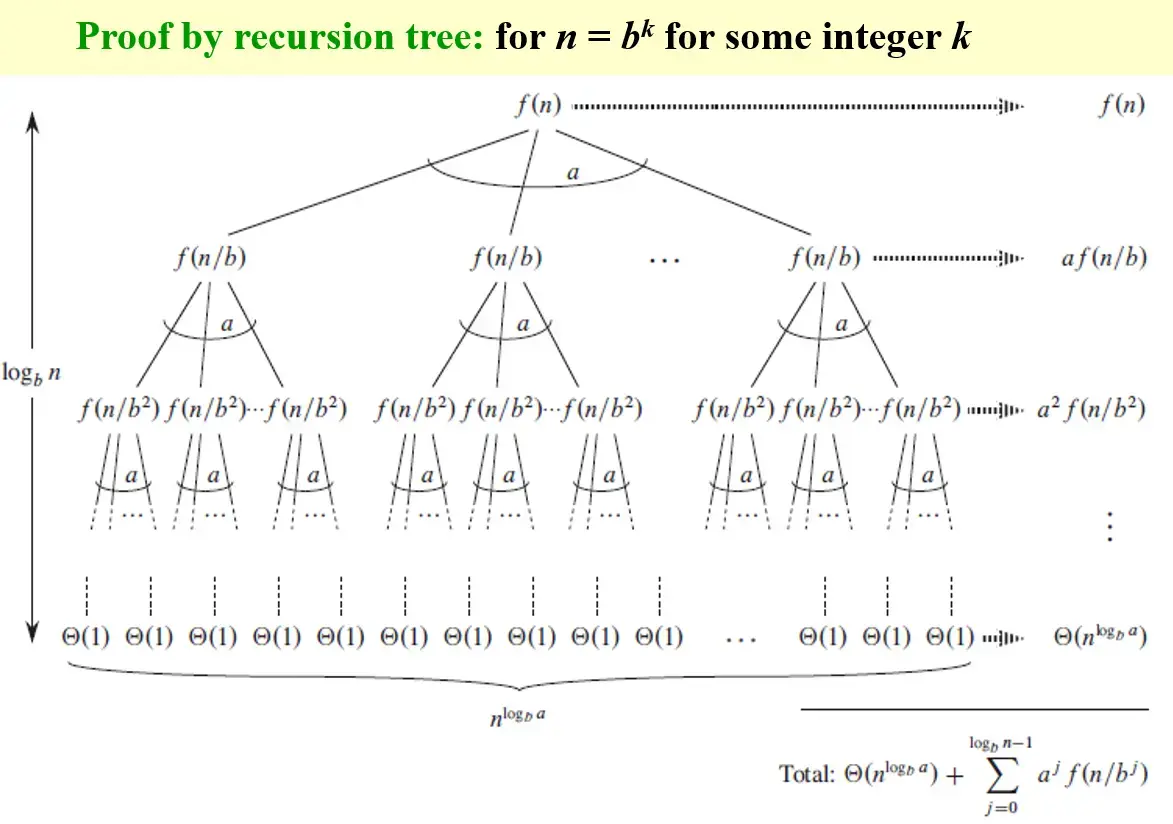
1. 如果存在常数 \(k<1\)，使得 \(af(N/b)=kf(N)\)，那么 \(T(N)=\Theta(f(N))\)
2. 如果存在常数 \(K>1\)，使得 \(af(N/b)=Kf(N)\)，那么 \(T(N)=\Theta(N^{\log_{b}a})\)
3. 如果 \(af(N/b)=f(N)\)，那么 \(T(N)=\Theta(f(N)\log_{b}N)\)

Attention

这种形式的适用范围没有前一种那么广，例如：

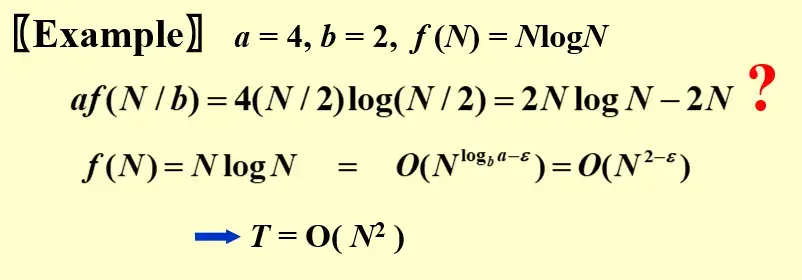
2.3.4 form 3

当 \(a\ge 1,b\geq 1, p\geq 0\) 时，对于递推式：

\[T(N)=aT(N/b)+\Theta(N^k \log^p N)\]

1. if \(a>b^k\), \(T(N)=O(N^{\log_{b}a})\)
2. if \(a=b^k\), \(T(N)=O(N^k \log^{p+1}N)\)
3. if \(a<b^k\), \(T(N)=O(N^k \log^p N)\)

Important

这种形式的使用场景最广，但仍然可以进行以下推广，使 \(p\) 为任意实数，则：

1. if \(a<b^k\), then
   1. if \(p<0\), \(T(N)=\Theta(N^k)\)
   2. if \(p\geq 0\), \(T(N)=\Theta(N^k\log^pN)\)
2. if \(a=b^k\), then
   1. if \(p<-1\), \(T(N)=\Theta(N^k)\)
   2. if \(p=-1\), \(T(N)=\Theta(N^k\log \log N)\)
   3. if \(p>-1\), \(T(N)=\Theta(N^k\log^{p+1}N)\)
3. if \(a>b^k\), \(T(N)=\Theta(N^{\log_{b}a})\)

3 Discussion

3.1 Three-way-mergesort

Question

Three-way-mergesort : Suppose instead of dividing in two halves at each step of the mergesort, we divide into three one thirds, sort each part, and finally combine all of them using a three-way-merge.

What is the overall time complexity of this algorithm for sorting n elements? Prove it.

How about \(k\)-way merge?

\(T(n)=kT(n/k)+O(n)\), where \(O(n)\) is merge time.

By Master theorem, \(a=k\), \(b=k\), \(f(n)=O(n)\), making \(\log_{b}a=1\), the recurrence relation falls under Case 2 of Master theorem, thus \(T(n)=\Theta(n^1\log n)=\Theta(n\log n)\)

3.2 Solve this recursion beyond master theorem

Question

\(T(n)=2T(|\sqrt{ n }|)+\log n\)

Let \(m=\log n\),
thus \(T(n)=2T(\sqrt{ n })+\log n \Rightarrow T(e^m)=2T(e^{m/2})+m\);
Let \(T_{1}(m)=T(e^m)\),
thus \(T_{1}(m)=2T_{1}(m/2)+m\);
By Master theorem, \(T_{1}(m)=T(e^m) = O(m\log m)\),
thus \(T(n)=O(\log n \cdot \log \log n)\)

conclusion

遇到 \(\sqrt{ N }\) 之类的，就进行代换

4 Questions

4.1 Q7

4.1.1 More about cloest pair of points

If devide-and-conquer strategy is used to find the closest pair of points in a plane, unless the points are sorted not only by their \(x\) coordinates but also by their \(y\) coordinates, it would be impossible to solve it in a time of \(O(N\log N)\), where \(N\) is the number of points.

Answer

T why? 难道不能先进行一个 \(O(N\log N)\) 的排序吗

4.2 HW7

4.2.1 Master theorem form3 利用

When solving a problem with input size \(N\) by divide and conquer, if at each stage the problem is divided into 8 sub-problems of equal size \(N/3\), and the conquer step takes \(O(N^2logN)\) to form the solution from the sub-solutions, then the overall time complexity is __.

Answer

\(O(N^2\log N)\) 因为 \(T(N)=8T(N/3)+O(N^2\log N)\)，其中 \(a=8,b=3,k=2,p=1\) 由于 \(a<b^k\)，所以 \(T(N)=O(N^k\log^pN)=O(N^2\log N)\)

4.3 Ex7

4.3.1 从代码使用 Master Theorem

Consider the following function, where the time complexity for function calc() is \(O(1)\).

void fun(int l, int r) {
    if(r-l+1<=1234) return;
    int m=(l+r)/2;
    int m1=(l+m)/2, m2=(m+1+r)/2;
    fun(l, m);
    fun(m1+1, m2);
    for(int k=1;k<=r-l+1;k++)
        for(int i=1;i<=r-l+1;i++)
            for(int j=l;j<=r;j+=i)
                calc(j, i);
    fun(m+1, r);
    fun(m1+1, m2);
}

Assume the initial input is l=1, r=N, What is the running time of this function? Your answer should be as tight as possible.

Answer

\(O(N^2\log^2N)\)

• Divide: 进行 4 次递归调用，每次的序列长度为 \(N/2\)
• Conquer:
  • for (int k = 1; k <= r - l + 1; k++) 这里有 \(N\) 次
  • for (int i = 1; i <= r - l + 1; i++) for (int j = l; j <= r - l + 1; j += i) 这里其实是 \(N(1+1/2+1/3+\dots+1/N)=N\log N\)
  • 因此，conquer 的总花销是 \(N^2\log N\)
• 依据 2.3.4 form 3 \(a=b^k\) 情况，得到 \(O(N^2\log^2N)\)

Comments