Skip to content

16 Query Optimization

Introduction#

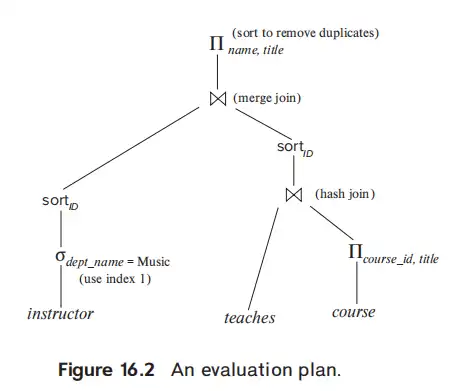
500x433

  • 执行计划，包括了算子的执行顺序（expression tree）和每一个环节的具体算法
  • 一个查询需求可能对应多种 expression tree，一个 expression tree 也可以对应多个 evaluation plan
  • 3 steps
    1. 根据 equivalence rules 生成一系列等价表达式
    2. 细化表达式的执行算法，找到对应的多种执行计划
    3. 找到最小的 estimated cost

Transformation of Relational Expressions#

  • euaivalent: 对于任意合法数据库，查询结果均相同

Equivalence Rules#

Examples of Transformations#

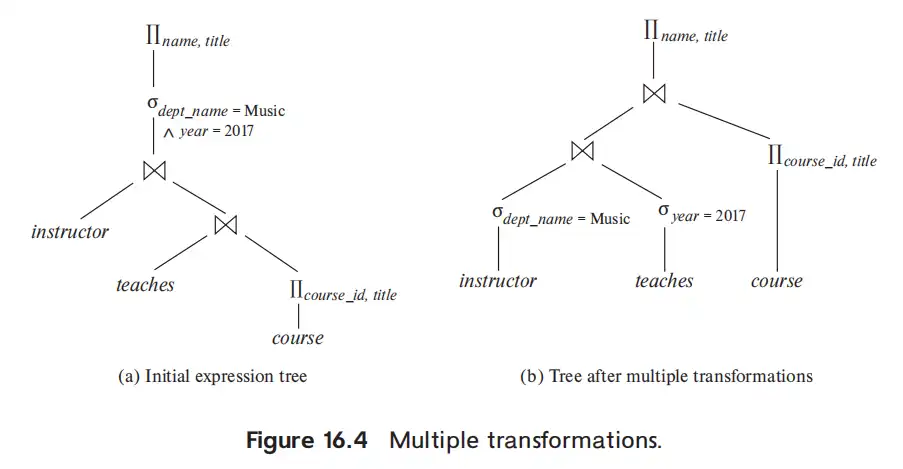
500x260

  • pushing selections: 提前选择操作，可以减少链接时 relation 的大小
  • pushing projection: 也是减小 join 时的大小
  • join ordering: 调整 join 的顺序也有助于减小 realtion 的大小

Enumeration of Equivalent Expressions#

500x247

  • 不断匹配 eq rules，添加新的表达式

Estimating Statistics of Expression Results#

Catalog Information#

  • \(n_r\): \(r\) 中元组数量
  • \(b_r\) blocks 数量， \(b_r=\lceil\frac{n_r}{f_r}\rceil\)
  • \(l_r\): 一个元组的 bytes 数量
  • \(f_r\): 一个 block 中能放下 (fit) 元组的数量
  • \(V(A,r)\): \(r\) 中属性 \(A\) 的不同取值的数量

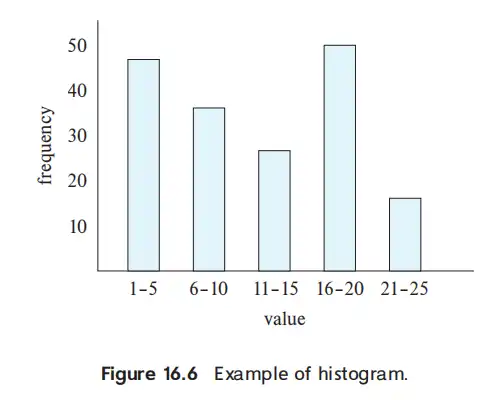
500x400

  • histogram
    • equi-width: 等间距
    • equi-depth: 使得 frequency 相等的间距

Selection Size Estimation#

Join Size Estimation#

  • Cartesian product \(r\times s\) 有 \(n_r\cdot n_s\) 个元素
  • \(R\cap S=\emptyset\), no common attr，就是 cartesian
  • \(R\cap S\) is a key for \(R\)，则 \(S\) 中一个 tuple 最多连接 \(R\) 中的一个 tuple，\(\leq n_s\)
  • \(R\cap S\) 不是 \(R\) 或 \(S\) 的 key，若 \(R\cap S=\{A\}\)
    • 平均下来，\(R\) 中一个 tuple 会产生 \(\frac{n_s}{V(A,s)}\) 个 tuple
    • 也就是 \(\frac{n_r\cdot n_s}{V(A,s)}\)，反过来就是 \(\frac{n_r\cdot n_s}{V(A,r)}\)，其中取更小的来估计更准确

Materialized Views#

Incremental View Maintainance#

  • 例如，\(v=r\bowtie s\)
  • 在 \(r\) 更新，如增加时，只需要考虑 \(r\) 中新增的 tuple 与 \(s\) 计算，在 \(v\) 中增加 tuple

Optimization#

  • 如果存在可用的 mv，可以替换查询表达式
  • 但是，考虑可能会进行 \(\sigma\) 选择操作，按照先选择的策略，可能用不到 mv