14 Indexing

Basic Concepts

• search key: 可以是单个或多个属性
• index file: 每个 entry 包含 [search_key, pointer]
• basic kinds of indices
  • ordered
  • hash: 通过 hash 将数据均匀分布在 buckets 中

Index Evaluation Metrics

• access types
  • point query
  • range query
• access time
• insertion time: 索引插入的维护时间
• deletion time: 索引删除的维护时间
• space overhead

Ordered Indices

• Clustering index: 聚集索引/主索引/primary index，search key 和 record 的顺序一样
• Secondary index: 辅助索引/nonclustering index，search key 定义的顺序和 record 顺序不同

Dense Index Files

• 表示所有的 search key 都出现在了索引文件中

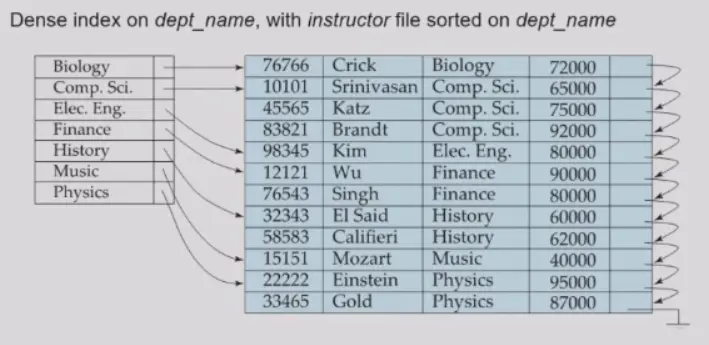
Sparse Index Files

• 只包含了部分 search key
  • 减少空间占用
  • 减少维护成本
• 查询时间更长了
• Good pracitce
  • 对于 clustered index，将 index 分 block，然后将每个 block 中保存最小的 search key
  • 对于 unclustered index，sparse index 必须是 dense index 的上层索引

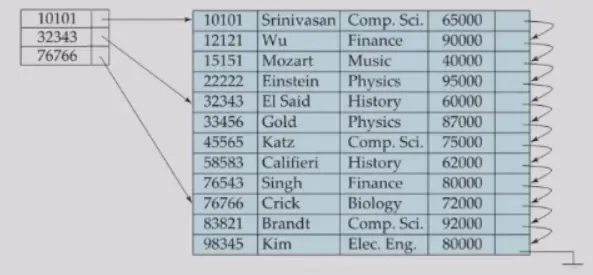
• more views
  • clustered index，顺序检索
  • secondary index，非顺序检索，跳读，导致 io 花销增大

Multilevel Index

如果索引文件仍然很大，也无法放在内存中

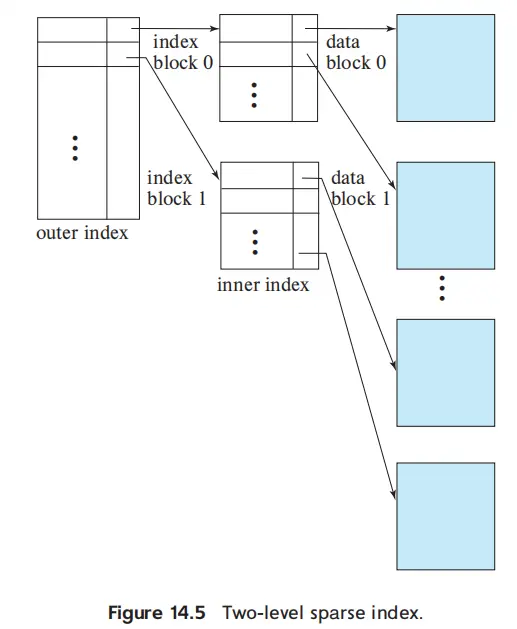
• inner index - basic index file
• outer index - a sparse index of the basic index
• 维护成本增大
• e.g. B+Tree

Index Update

Deletion

如果 index 中的 search key 对应的数据项被删除了，那么 index 中也需要删除

• dense index，直接删除
• sparse index
  • 如果下一个 search key 不在 index 中，则用其替换
  • 如果已经在 index 中，直接删除

Insertion

• single-level
  • dense index
    • 需要创建新的空间并插入，可能需要添加 overflow blocks
  • sparse index
    • 如果是 block of file 的 index，只有创建新的 block 时才插入
• multilevel: 类似 single-level

indices on multiple keys

multiple keys, e.g. (name, ID), 通过字典序排列

• query name or (name, ID) 都可以
• 查 ID 时索引无效，因为 ID 是乱的，可能还不如顺序扫描

可见 index 在有些情况下并没有用

B+ Tree Index Files

• indexed-sequential files 的维护代价比较大，需要周期性重组织
• B+ Tree 能够在 insert delete 时以较小的代价调整 index file 结构
  • 会有 perf overhead，但 minor

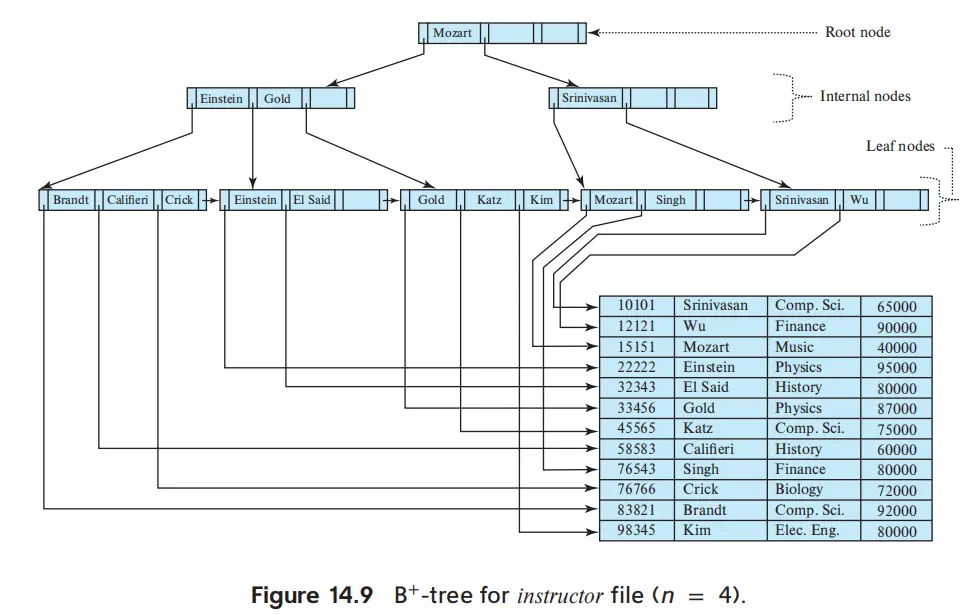
• order \(n\)，结构性质
  • 根节点
    • 孩子数量 \([2,n]\)
    • 作为叶子，\([0,n-1]\) value
  • 中间节点
    • 孩子数量 \([\lceil n/2 \rceil, n]\)
    • key 是右边指针指向的最小值
  • 叶子节点（非根）
    • 对应 entry 数量 \([\lceil (n-1)/2\rceil,n-1]\)
      • 记忆：二分之一向上取整
    • 最后一个指针指向下一个叶子节点
    • key 是左边指针指向的 entry 值
• \(Height\leq\lceil \log_{\lceil n/2\rceil} K\rceil\)，\(K\) 是文件的 search key value 数量

Non-Unique Keys

• 如果一个 key \(a_i\) non-unique，添加一个 key \(A_p\) 使得 \((a_i,A_p)\) 是唯一的
• 查找 \(a_i=v\) 相当于范围查找 \([(a_i, -\infty),(a_i, +\infty)]\)
• 但是会导致更多的 I/O
  • clustering，sequential
  • non-clustering，每个 record access 可能都需要一次 i/o

Complexity

• Worst case \(O(\log_{\lceil n/2\rceil} K)\)
• n 和 K 确定后，树的高度和插入顺序有关
  • insert in sorted order，每次都会导致一个 leaf full，分裂成 half full，就不会继续插入了，所以 occupancy = 0.5
  • insert in random order，occupancy = ⅔

B+ Tree Extensions

• file organization: 需要考虑 leaf node 的合并，可能一次要考虑更多的 leaf node
• secondary index
  • 辅助索引也需要更新，且代价很大
  • 也可以 secondary index 只保存 search key，查询的时候，通过 secondary index 找到 search key，再去 B+ tree 中查询对应的指针
• indexing strings
  • varible fanout，因为 string 是变长度的
  • string 还可以前缀压缩，减少空间占用
• B+ Tree disadvantages
  • 大量插入时，每次插入都需要多于一次 i/o，如何解决？
    • 先排序 external sort 再一个个插入，i/o 性能提升，但是大部分节点都 half full
    • 先排序，bottom-up 构建 B+ tree

Hash Indices

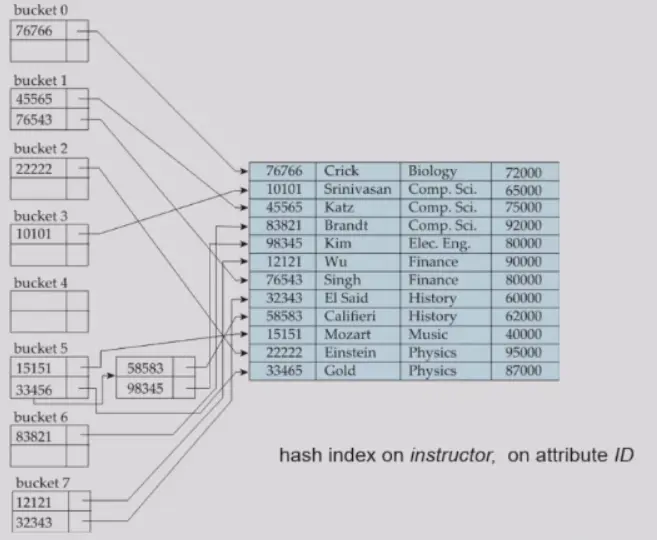
• hash function 的设计非常重要，与数据分布密切相关

Multiple-Key Access

• 要进行 where dept_name = 'Finance' and salary = 80000 查找时
  • 对 dept_name 做 index，然后检查 salary，或反之
  • 同时索引，效果更好
• where dept_name < 'Finance' and salary = 80000，这时 (dept_name, salary) 的索引就失效了

Other Features

• covering indices
  • 索引中可以有除了 search-key 之外的一些属性，且只保存在叶子节点中
  • 部分查询不需要取数据

Creation of Indices

CREATE INDEX <index-name> ON <relation-name> (<attr-list>)
DROP INDEX <index-name>

• 外键索引
  • 大多数数据库并不会自动创建
  • \(takes \bowtie \sigma_{name=Shankar}(student)\)，根据 student 查询到 id，然后用 id 查询 takes，如果有外键索引，效率会高很多

Write-Optimized Index Structures

• B+ tree 在随机插入时性能很低
  • 如果树过大，叶子节点的数量大于内存容量，每次随机访问叶子节点都很可能会导致 io
  • 参考 bottom-up b+ tree construct，就是顺序 io，关键在于将随机 io 变成顺序 io
• lsm tree:
• buffer tree: lazy writes, bulk processing

LSM Trees

支持高吞吐更新、写集中

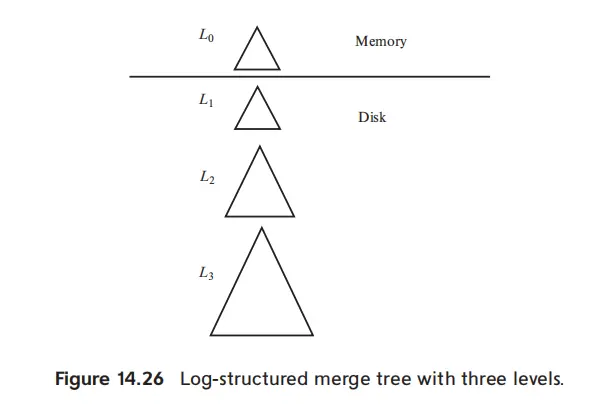
Insert

• 所有的 insert 都先插入到 L0
• 当 L0 满了，整个合并到 L1
  • 使用 bottom-up build 来进行 merge
  • 将 L1 的叶子读入内存，建树，写回 disk
• L1 超过一定 threshold，则合并到 L2

Pros and cons

• pros
  • 插入全都在内存操作，效率更高
  • io 都是顺序的
  • 叶子总是满的
• cons
  • 查询时需要遍历所有树
  • 合并时 copy 很多次
• stepped-merge index
  • 达到 threshold 才进行 merge，也就是每一层都有 k 个位置
  • bloom filter，树有一些标记，可以在查询时跳过部分树

Delete

• 加入一个特殊的 delete entry
• 在进行 merge 的时候可以同时遇到原 entry 和 delete entry，删掉这个 entry

Buffer Tree

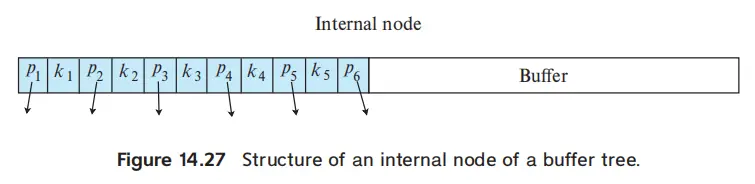
• 每个中间节点，包括根，都附带一个 buffer
• 插入
  • 找到最近的 buffer，记录在 buffer 里，buffer 中按 key 排好序
  • 当 buffer 满了再下推，也就是分发到孩子的 buffer 中
  • leaf 没有 buffer，就是执行正常的插入
  • leaf 分裂可能让 internal node 分裂，此时 buffer 也要分裂
• 查找
  • 相比普通的查找，多了一个检查叶子缓冲区的步骤
  • 同样可以使用范围查找（internal node 和 buffer 双指针完成）
• 删除和更新
  • 和 LSM 一样，通过加入 key 一样的删除和更新项来进行

最坏情况下，buffer tree 的 I/O 次数上界比 LSM 更低；读操作 buffer tree 更快，写操作 buffer tree 更差，因为需要更多的随机 I/O，寻道时间更多。因此，写操作多用 LSM tree，读操作多用 buffer tree

Bitmap Indices

方便进行多个条件的搜索

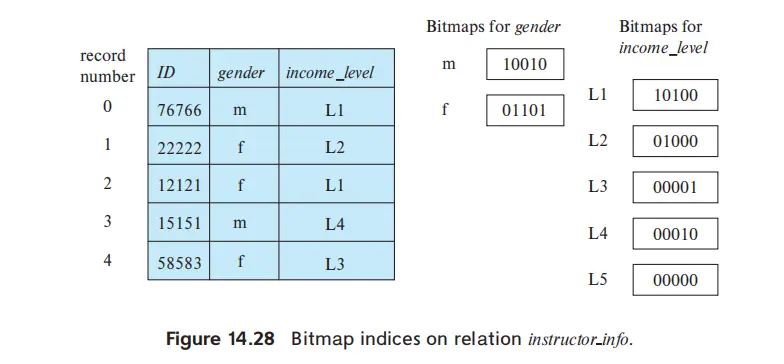
• 和 attr 的 domain 有很大关系
  • enum 比较方便编码
  • 连续的可以划分 level
• and or 都能直接进行位运算，sum 也可以直接计算 1 的数量