15 Query Processing

Overview#

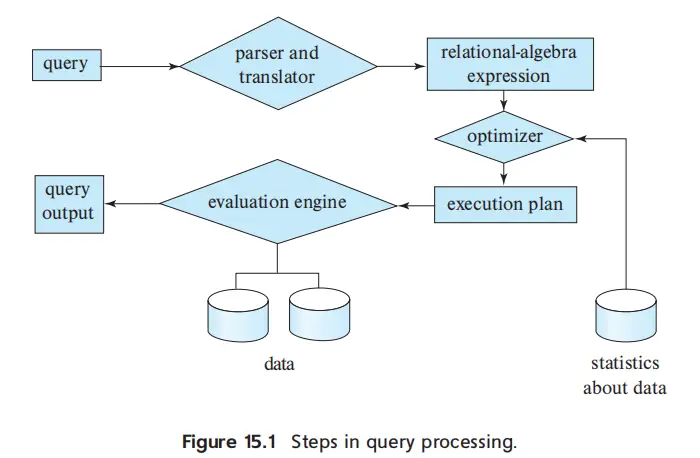
IMG-DB 15 Query Processing-20250429142938821.webp

exec-plan: annotated expr specifying detailed evaluation strategy
- e.g. use an index on salary to find instructors with salary < 75000

Measures of Query Cost#

factors
- disk, cpu, network

Disk#

factor: num of seeks/blocks read/block written
为了简单，用 seek 和 block transfer 来分析
- \(bt_T+St_S\)
- \(t_T, t_S\) 和硬件有关
进行 worst case 分析，假设初始 buffer 中没有任何数据

Selection Operation#

Using File Scans and Indices#

A1: Linear Search#

linear search: \(t_S+b_r t_T\)
linear search, equality on key: \(t_S+(b_r/2)t_T\)

A2: Clustering B+-tree Index, Equality on Key#

\((h_i+1)(t_T+t_s)\)
需要找到叶子节点，并读取数据所在 block，每次都要寻址和读

A3: Clustering B+-tree Index, Equality on Non-key#

\(h_i(t_T+t_S)+t_S+bt_T\)
找到位置后，顺序读 \(b\) 个块

A4: Secondary B+-tree Index#

equality on key: \((h_i+1)(t_T+t_S)\)
- 和 clustering 差不多
equality on non-key: \((h_i+n)(t_T+t_S)\)
- \(n\) 是取到的 record 数量，每个 record 都可能在不同且不连续的 block 上，所以认为每次都要寻址和传输

Selections Involving Comparisons#

A5: Clustering B+-tree Index, Comparison#

\(h_i(t_T+t_S)+t_S+bt_T\)
找到第一个满足的 key，然后顺序读 \(b\) 个块
和 A3 比较像

A6: Secondary B+-tree Index, Comparison#

\((h_i+n)(t_T+t_S)\)
找到第一个满足的 key，然后读 \(n\) 个 record
和 A4 比较像

Implementation of Comploex Selections#

考虑多个 selection condition 的逻辑运算，包括 conjunction, disjunction, negation

A7: Conjunctive Selection Using One Index#

首先检查是否有能通过 A2-A6 进行计算的简单条件，如果有则先用成本最低的方法运算
剩下的部分，从前面的结果中 fetch and check

A8: Conjucntive Selection Using Composite Index#

如果存在可用的复合索引，就使用 A2-A4 中的算法进行激素那

A9: Conjunctive Selection by Intersection of Identifiers#

索引有 record ptr，首先利用各个条件得到 sets of record ptrs
然后计算交集，再从文件中取
没有 index 的 condition 还是 fetch and check

A10: Disjunctive Selection by Union of Identifiers#

和 A9 类似，用并集

P.S. Negation

linear search
如果有 index，而且满足 \(\neg\theta\) 的 record 数量非常少，可以用 index

Sorting#

Exteranl Sort-Merge Algorithm

Stage 1. Run Sorting#

每次读取 \(M\) 个 block 到 buffer，进行 in-memory sorting
排好序的一组称为 run，保存为 run file \(R_i\)
run file 的保存有两种策略
- early materialization: 存储实际数据
- late materialization: 存储 sort key 和 ptr(record ID)

Stage 2. Merge#

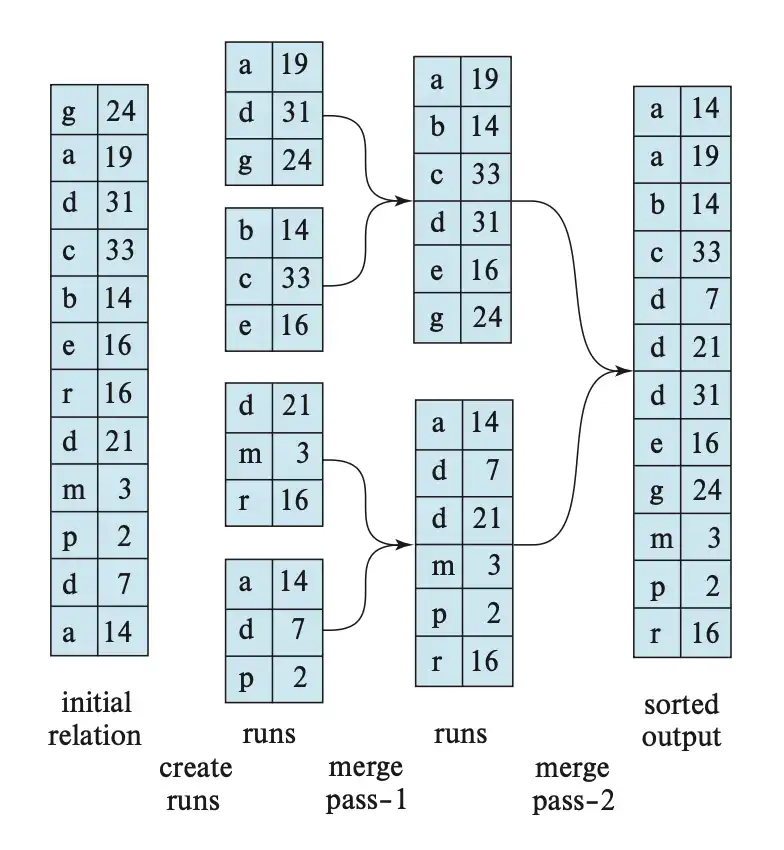
500x542

假设一共有 \(N\) 个 run file，考虑 output buffer，每趟最多将 \(M-1\) 个 run 作为输入
若 \(N<M\)，每个 run 都能分配到一个 input buffer，进行一次 N-way merge 即可
但一般情况下 \(N>M\)，此时要用多趟合并
- 每一趟最多将 \(M-1\) 个 run 合并为 1 个 run，也就是 run 数量减少到 \(\frac{1}{M-1}\)
- 可以将初始创建 run 的过程视作 pass 0，pass 数量的计算方法为：\(\text{\# passes}=1+\lceil \log_{M-1} \lceil N/M\rceil\rceil\)

Cost Analysis#

假设 relation 有 \(b_r\) 个 block，为了减少 seek 数量，每次读写 \(b_b\) 个 block，忽略最终结果写回的任何开销
block transfer
- run sorting: \(2b_r\)，因为需要读取并写回这么多数据
- merge
  - 每一趟合并了 \(\lfloor M/b_b-1\rfloor\) 个 run
  - 总合并趟数 \(\lceil \log_{\lfloor M/b_b-1 \rfloor} (\frac{b_r}{M})\rceil\)
  - 每趟都需要读写整张表大小的数据，所以 \(2b_r \lceil \log_{\lfloor M/b_b-1 \rfloor} (\frac{b_r}{M})\rceil\)
- 考虑忽略最终结果的写回操作开销 (\(-b_r\))，则总 block transfer \(b_r(2 \lceil \log_{\lfloor M/b_b-1 \rfloor} (\frac{b_r}{M})\rceil+1)\)

Note

如果使用 LIMIT 语句，只查询 top-N，可以维护一个大小为 N 的 heap，并使用线性扫描

Join Operations#

\(r\bowtie_{r.A=s.B} s\)
同样忽略最终结果的任何开销

Nested-Loop Join#

for all tuple tr in r do
    for all tuple ts in s do
        test pair (tr, ts) to see if the join condition theta is satisfied
        if so, add tr * ts to the result
    end for
end for

假设 \(r\) 是外层关系
最好情况下，内存能容纳两张表
- block transfer: \(b_r+b_s\)
- seek: \(2\)
最坏的情况下，内存只能为每个关系保存一个块
- block transfer: \(b_r+n_r b_s\)
- seek: \(b_r+n_r\)
如果内存能保存一个完整的关系，最好将内层关系完整保存，也是最好的
- block transfer: \(b_r+b_s\)
- seek: \(2\)

Block Nested-Loop Join#

按照块读取关系，节省块的访问次数
最好情况下，内存能够容纳内层关系
- block transfer: \(b_r+b_s\)
- seek: \(2\)
最坏情况下，仍然只能各容纳一块
- block transfer: \(b_r+b_rb_s\)
- seek: \(2b_r\)
一般情况下，每次从外层循环读取尽量多的内存块，减少内层的读取次数
- block transfer: \(b_r+\lceil\frac{b_r}{M-2}\rceil b_s\)
- seek: \(2\lceil\frac{b_r}{M-2}\rceil\)

Indexed Nested-Loop Join#

for all tuple r in R do
    for all tuple s in Index(ri = sj) do
        if r and s match then
            add r * s to the result
        end if
    end for
end for

对于外层关系 r 的每一个元组，都对 s 的索引进行一次查找
最坏情况下，仅容纳 r 的一个块和 index 的一个块，链接成本为 \(b_r(t_T+t_S)+n_rc\)，其中 \(c\) 是从 s 中进行索引和数据读取的开销

Merge Join#

流程
- r 和 s 先按照 join attr 排好序
- 使用双指针法判断是否需要 join，并写入 result
假设为了减少随机 I/O，分配了 \(b_b\) 个缓存块
- block transfer: \(b_r+b_s\)
- seek: \(\lceil b_r/b_b\rceil+\lceil b_s/b_b\rceil\)

Hybrid Merge-Join#

如果一个关系已经排序了，另一个在 join attr 上有 secondary index：

将 sorted relation 和 B+tree leaf entries 进行 merge
对来自 index 的 tuple 的物理地址进行排序
按照顺序访问这个 relation，减少 I/O，得到结果

Hash Join#

类似 merge，都是进行局部的判断来减少比较次数，进行 equi-joins 和 natural join
内存分配
- 假设划分为 \(n_h\) 个 bucket，考虑到希望每个 bucket 都能一次性读入内存，所以 \(n_h\) 要足够大，至少为 \(\lceil b_s/M\rceil\)
- 又希望内存里能够放下 \(n_h\) 个 buffer，这样不用递归划分，所以至少 \(M>n_h\)
- 综上 \(M^2>b_s\) 的时候不用递归划分
- 这里的 \(b_s\) 可以选择比较小的一张表
Partitioning
- 对于 \(s,r\) 中的元组，进行 hash 划分，得到 \(n_h\) 个 \(H_s\) 和 \(H_r\) buckets
- 在 \(M^2<b_s\) 的情况下，由于 \(n_h>M\)，第一轮的 bucket 存的可能不是单一 hash value 而是 hash value 在一个区间内的值，所以需要递归划分
  - 无论怎样，确保最终一个 bucket 能够放在内存中 \(n_h\geq \lceil b_s/M \rceil\)
    - 但即使满足了这个等式，也可能出现偏斜划分，导致部分 bucket 大小超出内存容量，所以一般划分数量要再多 20%
join
- 每次从 \(H_s\) 中取一个 bucket 放入内存，取 \(r\) 对应的 bucket（不一定都能放入内存）
Cost
- 如果不用递归划分
  - 划分需要 \(2(b_r+b_s)+2n_h\) 次传输，join 需要 \(b_r+b_s+2n_h\) 次传输，总共 \(3(b_r+b_s)+4n_h\) 次传输，其中 \(4n_h\) 基本可以忽略
  - 假设缓冲区大小是 \(b_b\)，划分需要寻道 \(2(\lceil b_r/b_b\rceil+\lceil b_s/b_b\rceil)\) 次，join 需要 \(2n_h\) 次，一共 \(2(\lceil b_r/b_b\rceil+\lceil b_s/b_b\rceil)+2n_h\) 次
- 需要递归划分
  - 每次递归，划分数量增加 \(\lceil M/b_b-1\rceil\) 倍，一共需要 \(\lceil \log_{\lfloor M/b_b -1\rfloor}\frac{b_s}{M}\rceil\) 趟
  - 总传输次数 \(2(b_r+b_s)\lceil \log_{\lfloor M/b_b -1\rfloor}\frac{b_s}{M}\rceil +b_r+b_s\)
  - 总寻道次数 \(2(\lceil b_r/b_b\rceil+\lceil b_s/b_b\rceil)\lceil \log_{\lfloor M/b_b -1\rfloor}\frac{b_s}{M}\rceil\)
  - 都已经忽略了 bucket 多余一些和 bucket 寻道的少量开销

Query Processing in Memory#

Cache-Conscious Algorithms#

目标是减少 cache miss

sorting -