07 Relational Database Design
Sumarry
引入范式理论,评估数据库设计的好坏
Features of Good Relational Designs#
- 如果只是保存 instructor 和 department 的 natural join 的表,则有信息重复、更新困难的缺点,所以需要 decomposition
Decomposition#
将一个 schema 分解成两种 schema
- 有损分解 (lossy decomposition)
- \(r\subset\Pi_{R_1}(r)\bowtie\Pi_{R_2}(r)\)
- e.g.

- 如果有重名,就会有信息损失
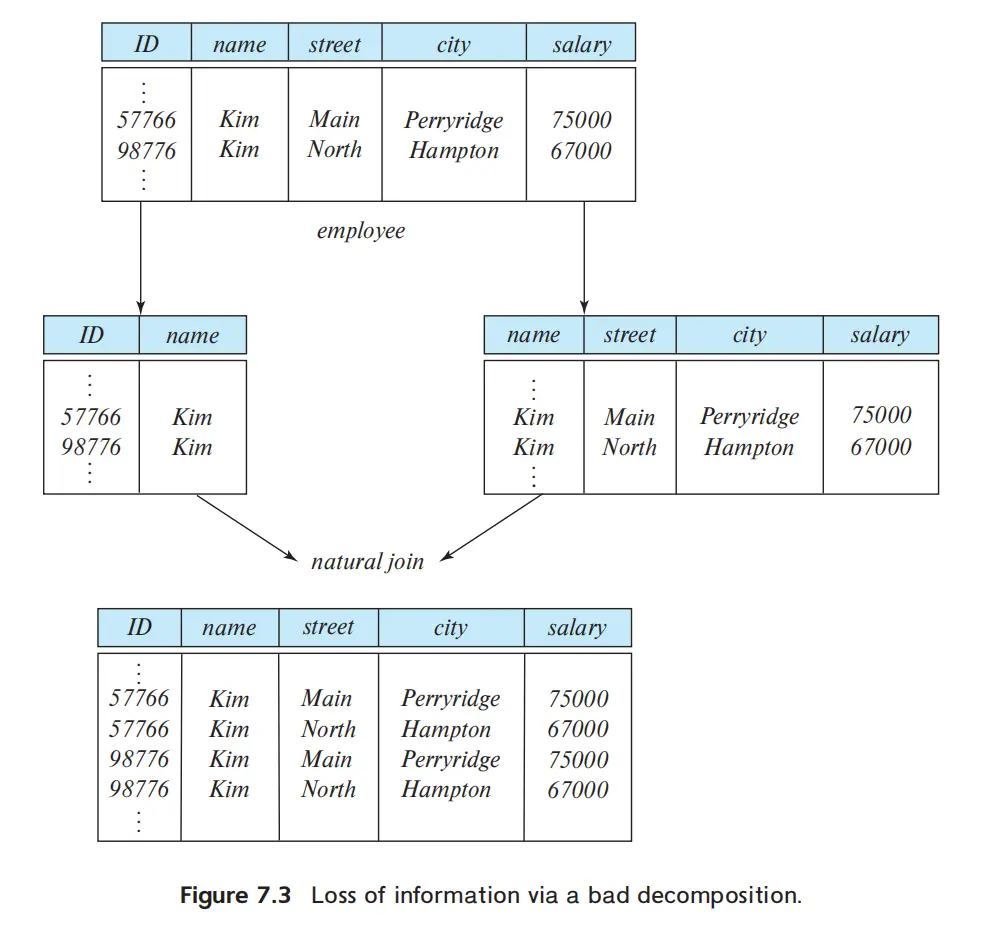
- 如果有重名,就会有信息损失
- 无损分解 (lossless decomposition)
- \(\Pi_{R_1}(r)\bowtie\Pi_{R_2}(r)=r\)
Question
分解是否无损,如果事后检查,成本很高而且不可恢复;本章主要研究如何快速判断无损分解
Normalization Theory#
- 判断一个 relation 是否是 good form
- 如果一个 relation 不是 good form,进行分解,使得
- 每个子 relation 都是 good form
- lossless decomposition
Functional Dependencies#
- Functional Dependencies
- schema \(R\), let \(\alpha\subseteq R, \beta\subseteq R\)
- functional dependency \(\alpha\rightarrow\beta\) 表示 \(\alpha\) 确定 \(\beta\),\(\alpha\) 相等则 \(\beta\) 相等
- 如果对于所有 \(r(R)\) 的 instance,都有 \(\alpha\rightarrow\beta\) 成立,则 \(r(R)\) 满足函数依赖 \(\alpha\rightarrow\beta\)
- e.g. dept_name -> building, ID -> building
- Different Functional Dependencies
- 如果 \(\beta\subseteq\alpha\),则显然 \(\alpha\rightarrow\beta\),称为 trivial functional dependency
- closure of \(F, F^+\)
- e.g. A->B, B->C, then A -> C, AB -> B, ... 大多数都是 trivial,指数复杂度
Lossless Decomposition#
将 \(R\) 分解为 \(R_1, R_2\), 分解无损若至少有一个成立(也就是 \(\in F^+\))
- \(R_1\cap R_2\rightarrow R_1\)
- \(R_1\cap R_2\rightarrow R_2\)
换句话说,要求 \(R_1\cap R_2\) 是 \(R_1\) 或 \(R_2\) 中的一个 superkey
Example

Dependency Preservation#
依赖保持:在测试一个函数依赖时只用考虑一个 relation
Normal Forms#
Boyce-Codd Normal Form#
- definition: 对于 \(R\),在其 \(F^+\) 中所有形似于 \(\alpha\rightarrow\beta\) 的函数依赖,都能至少满足以下一个条件,则 \(R\) in BCNF
- \(\alpha\rightarrow\beta\) is trivial
- \(\alpha\) is a superkey of \(R\)
- decomposition: 对于所有使得 \(R\) 不是 BCNF 的 \(\alpha\rightarrow\beta\)
- 将 \(R\) 分解为 \(\alpha\cup\beta\) 和 \(R-(\beta-\alpha)\),于是能够保证 \(\alpha\cup\beta\) 是 BCNF
- 使用 BCNF 进行分解,不能保证 dependency preserving
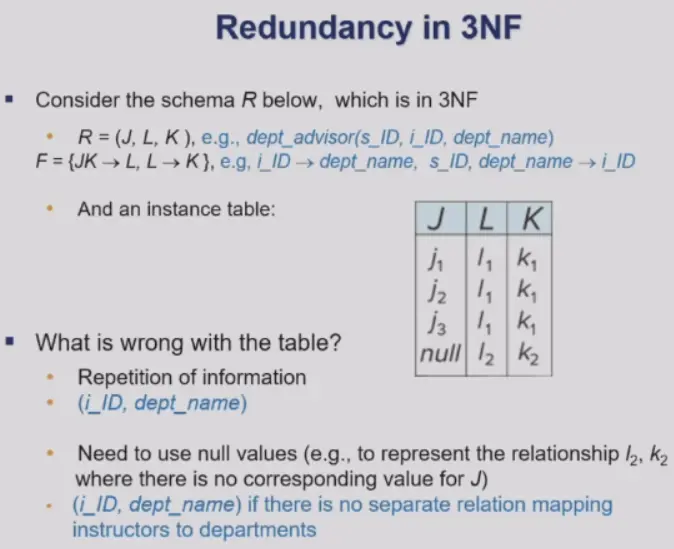
Thrid Normal Form#
- definition: 对于 \(R\),在其 \(F^+\) 中所有形似于 \(\alpha\rightarrow\beta\) 的函数依赖,都能至少满足以下一个条件,则 \(R\) in BCNF
- \(\alpha\rightarrow\beta\) is trivial
- \(\alpha\) is a superkey of \(R\)
- \(\beta-\alpha\) 中的每一个 attr \(A\) 都包含在 \(R\) 的一个 candidate key 中
- 如果 \(R\in BCNF\) 那么 \(R\in 3NF\),放宽了 BCNF 的约束
- tradeoff
- pros: 确保 dependency preserving
- cons: 存在信息冗余,重复 or NULL
回顾目标
- 每个 relation 都是 good form
- 分解时 lossless 的
- 分解最好是 dependency preserving 的
Functional-Dependency Theory#
Closure of \(F\)#
- closure of a set of functional dependencies \(F^+\)
- 重复使用 Armstrong's Axioms, these rules are sound(正确有效的) and complete(完备的)
- reflexive rule (自反): if \(\beta\subseteq\alpha\), then \(\alpha\rightarrow\beta\)
- augmentation rule (增补): if \(\alpha\rightarrow\beta\), then \(\gamma\alpha\rightarrow\gamma\beta\)
- transitivity rule (传递): if \(\alpha\rightarrow\beta\) and \(\beta\rightarrow\gamma\), then \(\alpha\rightarrow\gamma\)
- additional rules
- union rule: if \(\alpha\rightarrow\beta\) and \(\alpha\rightarrow\gamma\), then \(\alpha\rightarrow\beta\gamma\)
- decomposition rule: if \(\alpha\rightarrow\beta\gamma\), then \(\alpha\rightarrow\beta\) and \(\alpha\rightarrow\gamma\)
- pseudotransitivity rule: if \(\alpha\rightarrow\beta\) and \(\gamma\beta\rightarrow\delta\), then \(\alpha\gamma\rightarrow\delta\)
Closure of \(\alpha\)#

可以用来判断 \(\alpha\) 是不是 candicate key
- 若 \(\alpha^+=R\),则 \(\alpha\) 是一个 super key
- 其次再证明在 \(\alpha\) 中减少任意一个 attr,都不能得到 \(\alpha^+=R\)

Uses of Attr Closure#
- 测试是否为 superkey (e.g. in BCNF, trivial?, \(\alpha^+=R\)?)
- 测试函数依赖 (e.g. \(\alpha^+=\{A,B\}\), \(\alpha\rightarrow A, \alpha\rightarrow B\))
- 计算 \(F^+\) (计算 \(R\) 的所有子集 \(\gamma\),都计算 \(\gamma^+\),得到所有函数闭包)
Canonical Cover#
试图找到 \(F^+\) 等价的最小子集 \(F_c\),便于进行 decomposition 验证
满足以下条件的 \(F_c\)
- \(F_c^+=F^+\),即 \(F_c\) 与 \(F\) 等价
- \(F_c\) 中所有依赖都没有 extraneous attr
- \(F_c\) 中每个依赖的每一侧都是不同的
- 例如,\(\alpha\rightarrow\beta_1, \alpha\rightarrow\beta_2\) 应该简化成 \(\alpha\rightarrow\beta_1\beta_2\)

Extraneous Attributes#
extraneous attributes (无关属性): 删除后不会改变 \(F^+\) 的属性
- 对于 \(\alpha\rightarrow\beta\in F\)
- insight: 在左侧删除,依赖 stronger;右侧删除,依赖 weaker
- remove from the left side: \(A\in\alpha\) is extraneous in \(\alpha\) if \(F\) 能够推导出 \((F-\{\alpha\rightarrow\beta\})\cup\{(\alpha-A)\rightarrow\beta\}\)
- 也就是在 \(F\) 中将 \(\alpha\rightarrow\beta\) 换成了 \((\alpha-A)\rightarrow\beta\) 后仍然等价,只是推导到 \(F\) 是显然的所以不考虑
-
只用检查\(\beta\subseteq(\alpha-\{A\})^+\)
- remove from the right side: \(A\in\beta\) is exttraneous in \(\beta\) if \((F-\{\alpha\rightarrow\beta\})\cup\{\alpha\rightarrow(\beta-A)\}\) 能够推导出 \(F\)
-
只用检查\(A\in\alpha^+\)
-
Dependency Preservation#
-
将\(R\) 分解成 \(R_1, R_2, \dots, R_n\),若 \((F_1\cup F_2\cup\dots\cup F_n)^+=F^+\),那么这个分解是 dependency preserving 的
- \(F_i\) 表示 \(F\) 在 \(R_i\) 上的 restriction,是 \(F\) 中只包含 \(R_i\) 中 attr 的依赖的集合
Testing#

Algorithms for Decomposition#
BCNF Decomposition#
- BCNF 测试,检查一个分解 \(R_i\) 是否都满足 BCNF
- 测试 \(F^+\) 中,所有 FDs 左右都包含在 \(R_i\) 的依赖子集
- algo:

e.g. relation(1, 2, 3, ..., 11)
- FDs
- 1 -> 2,3,4
- 8,9 -> 10
- 1,5,6,7 -> 8,9,11
- result: (1, 2, 3, 4), (8, 9, 10), (1, 5, 6, 7, 8, 9, 11) 先用 FD1,再用 FD2
3NF Decomposition#
- motivation: 有些情况下 BCNF 没有 dependency preservation
- testing
- NP-hard: 因为需要查找 candidate keys
- 但是分解只需要多项式时间
- algo:

- 简单解释
- 首先将所有 \(F_c\) 中的依赖都建表
- 如果没有一张表中出现了 candidate key,那么加一张表存 candidate key
- 去重,保证 \(R_i\) 互不为子集
- dependency preservation: 因为对于 F 中的每个 dependency,都建立了表,总能在一张表中验证
- 总是保存了 candicate key for R,所以是无损的
- 简单解释
| BCNF | 3NF |
|---|---|
| lossless | lossless |
| may not dependency preservation | dependency preservation |
Note
数据库仅仅实现了 superkey,因为 FD 的验证花费很大
Decomposition Using Multivalued Dependencies#
BCNF 的缺陷

- 这个例子满足了 BCNF
- 但是仍然能够再分解为 inst_child, inst_phone
Multivalued Dependencies#
Definition 1
\(\alpha\rightarrow\rightarrow\beta\) 表示 \(\alpha\) 多值确定了 \(\beta\),if 存在 \(t_1[\alpha]=t_2[\alpha]\) 且存在 \(t_3, t_4\) 使得:
- \(t_1,t_2,t_3,t_4\) 的 \(\alpha\) 相等
- \(t_1,t_3\) 和 \(t_2,t_4\) 的 \(\beta\) 相等
- \(t_1,t_4\) 和 \(t_2,t_3\) 的 \(R-\alpha-\beta\) 相等
- 或者说,\(\beta\) 和 \(R-\alpha-\beta\) 是独立的
Definition 2
或者将 \(R\) 分解为非空的三个集合 \(Y,Z,W\),如果 \(<y_1,z_1,w_1>\in R \land <y_1,z_2,w_2>\in R\Rightarrow <y_1,z_1,w_2>\in R \land <y_1,z_2,w_1>\in R\),那么 \(Y\rightarrow\rightarrow Z, Y\rightarrow\rightarrow W\)
- FD 是 MVD 的特殊情况,if \(\alpha\rightarrow\beta\), then \(\alpha\rightarrow\rightarrow\beta\)
- MVD 集合 \(D\),闭包为 \(D^+\)
4NF#
Definition
\(R\) is in 4NF, if \(\forall \alpha\rightarrow\rightarrow\beta \in D^+\):
- \(\alpha\rightarrow\rightarrow\beta\) is trivial
- \(\alpha\) is a superkey for \(R\)
- if R in 4NF, then R in BCNF 4NF 更加严格


Additional Issues#
- first normal form: domain is atomic if its elements are considered to be indivisible units
- project-join normal form (5NF)
- ER 模型设计的好,不应该需要 normalization 优化