Skip to content

12 Animation

Mass Spring System#

A Simple Spring#

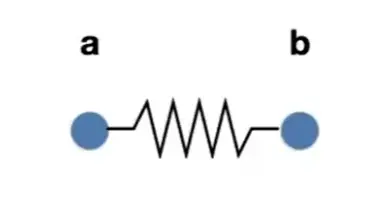
311x161

\[\begin{aligned} & \boldsymbol{f}_{a\to b}=k_S(\boldsymbol{b}-\boldsymbol{a}) \\ & \boldsymbol{f}_{b\to a}=-\boldsymbol{f}_{a\to b} \end{aligned}\]

考虑弹簧原长度：

\[\boldsymbol{f}_{a\to b}=k_S\frac{\boldsymbol{b}-\boldsymbol{a}}{||\boldsymbol{b}-\boldsymbol{a}||}\left(||\boldsymbol{b}-\boldsymbol{a}||-l\right)\]

考虑弹簧上的微小摩擦：

\[f_{\boldsymbol{b}}=-k_d\frac{\boldsymbol{b}-\boldsymbol{a}}{\|\boldsymbol{b}-\boldsymbol{a}\|}(\dot{\boldsymbol{b}}-\dot{\boldsymbol{a}})\cdotp\frac{\boldsymbol{b}-\boldsymbol{a}}{||\boldsymbol{b}-\boldsymbol{a}||}\]

Structures from Springs#

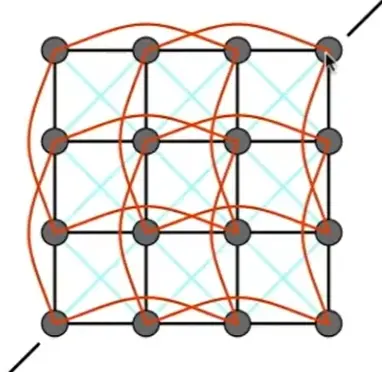
311x303

Note

能够保证在拉伸、压缩、翻折的时候都会导致部分弹簧长度变化，从而能自发稳定到平面形态

Note

Finite Element Method (FEM) 也可以用来实现类似的效果

Particle Systems#

  • 每个粒子的运动都取决于外力作用
  • 可能需要很多的粒子，以及邻居搜索的数据结构

Simulated Flocking#

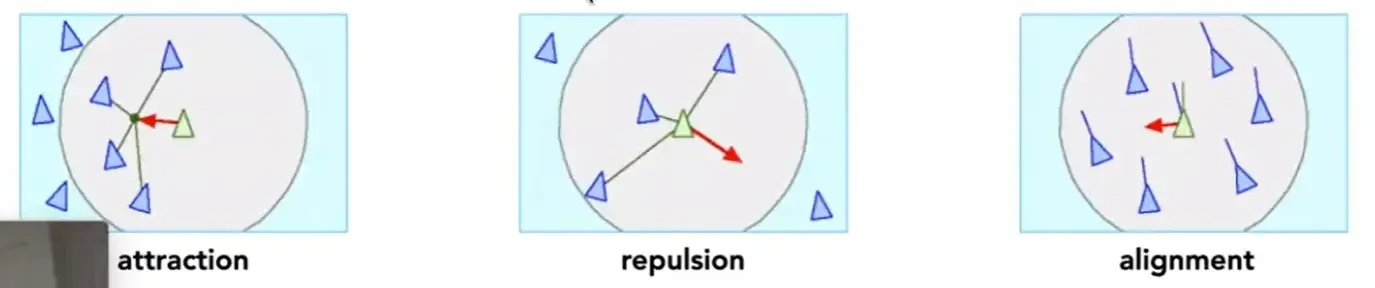
605x128

Note

定义个体和群体之间的关系，状态更新

Kinematics#

Forward#

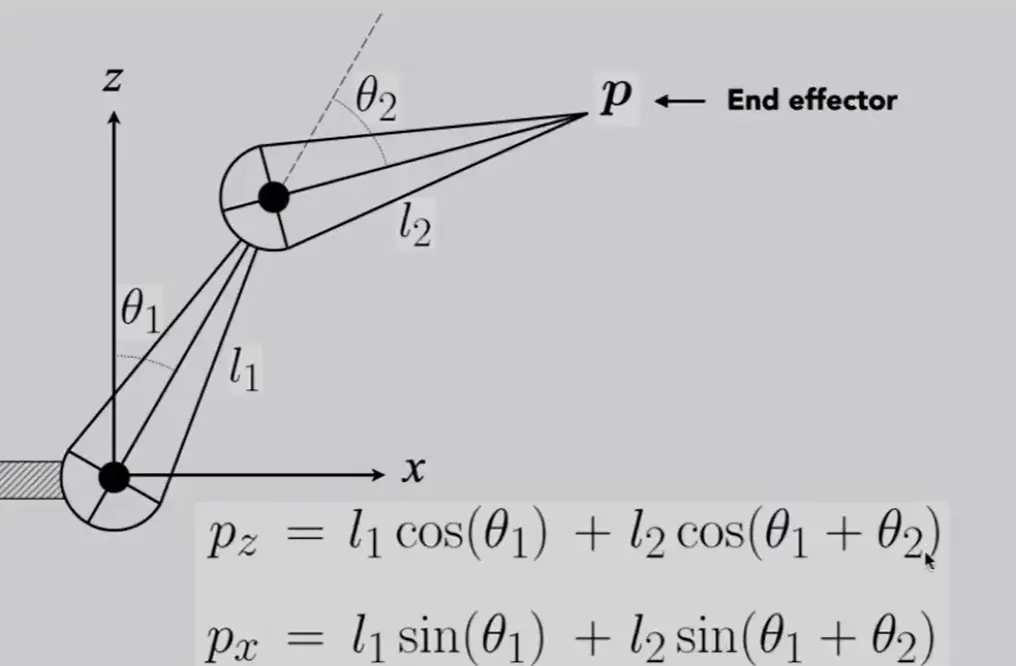
414x271

Inverse#

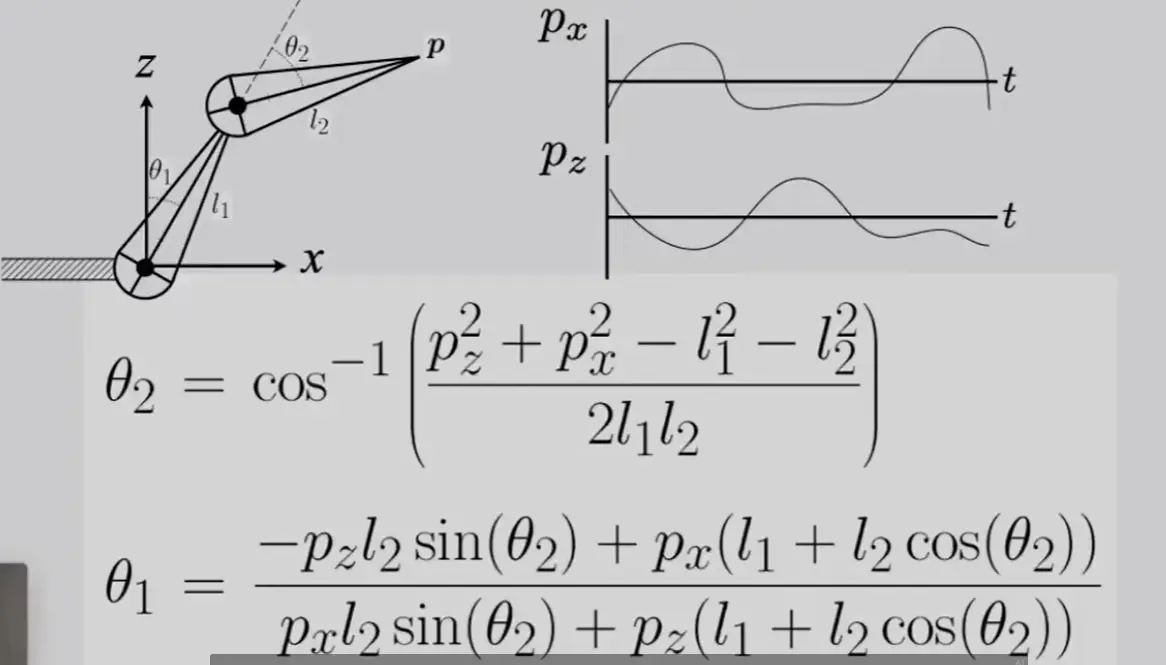
500x285

Note

  • 可能没有唯一解，可能没有解
  • 可以使用优化法来解方程

Rigging#

例如通过控制骨骼或者可动单元的控制点，来控制人物姿势或表情

Motion Capture#

Facial Motion Capture#

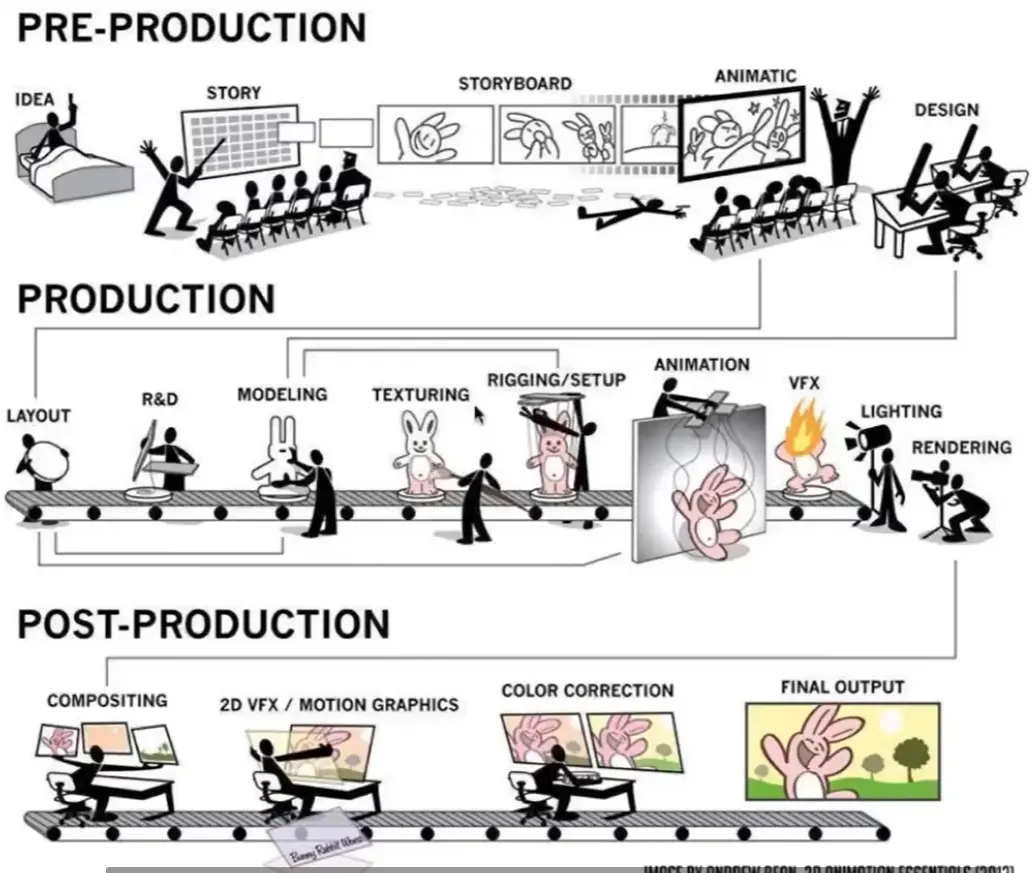
Production Pipeline#

500x422

Single Particle Simution#

模拟一个粒子在速度场中的运动

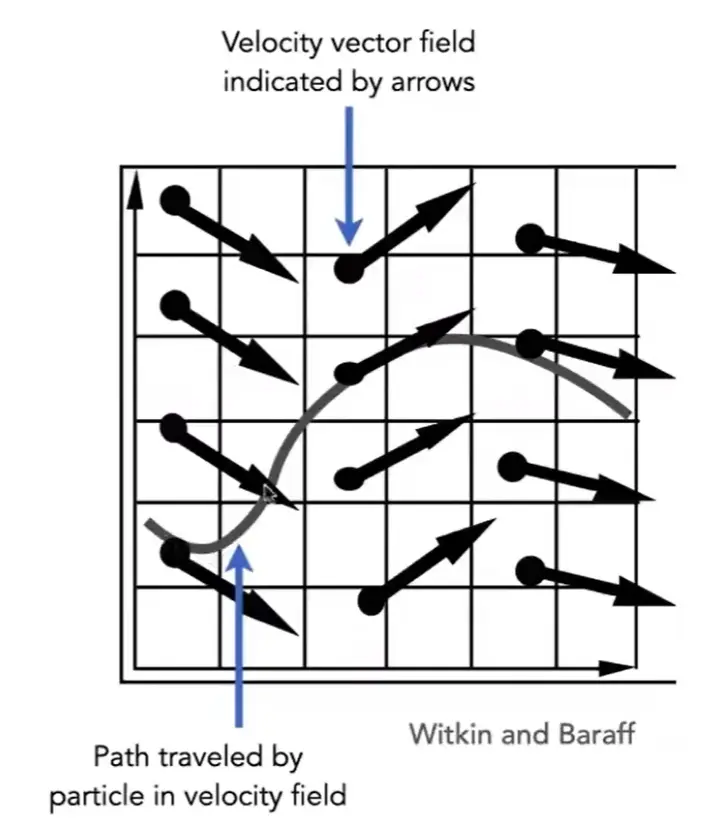
376x431

常微分方程：

\[\frac{\mathrm{d}x}{\mathrm{d}t}=\dot{x}=v(x,t)\]

Euler's Method#

\[\begin{aligned}\boldsymbol{x}^{t+\Delta t}&=\boldsymbol{x}^t+\Delta t\boldsymbol{\dot{x}}^t\\\boldsymbol{\dot{x}}^{t+\Delta t}&=\boldsymbol{\dot{x}}^t+\Delta t\boldsymbol{\ddot{x}}^t\end{aligned}\]

Note

  • simple iterative
  • commonly used
  • very inaccurate
  • most often goesunstable

Errors#

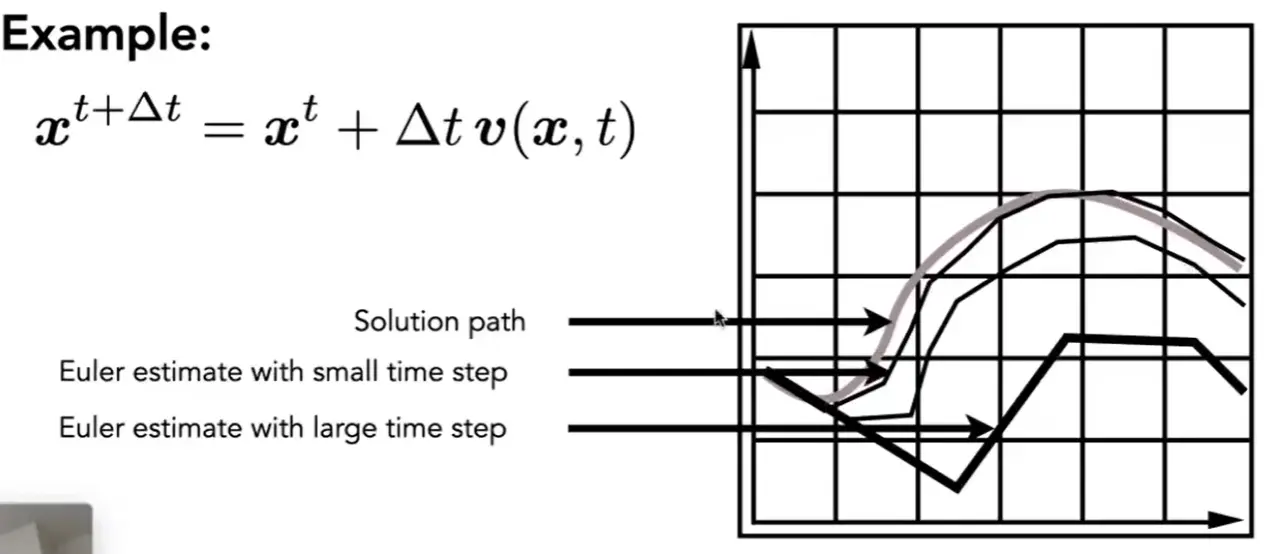
500x219

Note

减小 \(\Delta t\) 能够减小误差

Instability#

500x303

Note

  • 误差会积累，造成模型发散
  • 实际运用中，误差可以在一定程度上忽略，但是不稳定性不可被忽略

Midpoint Method#

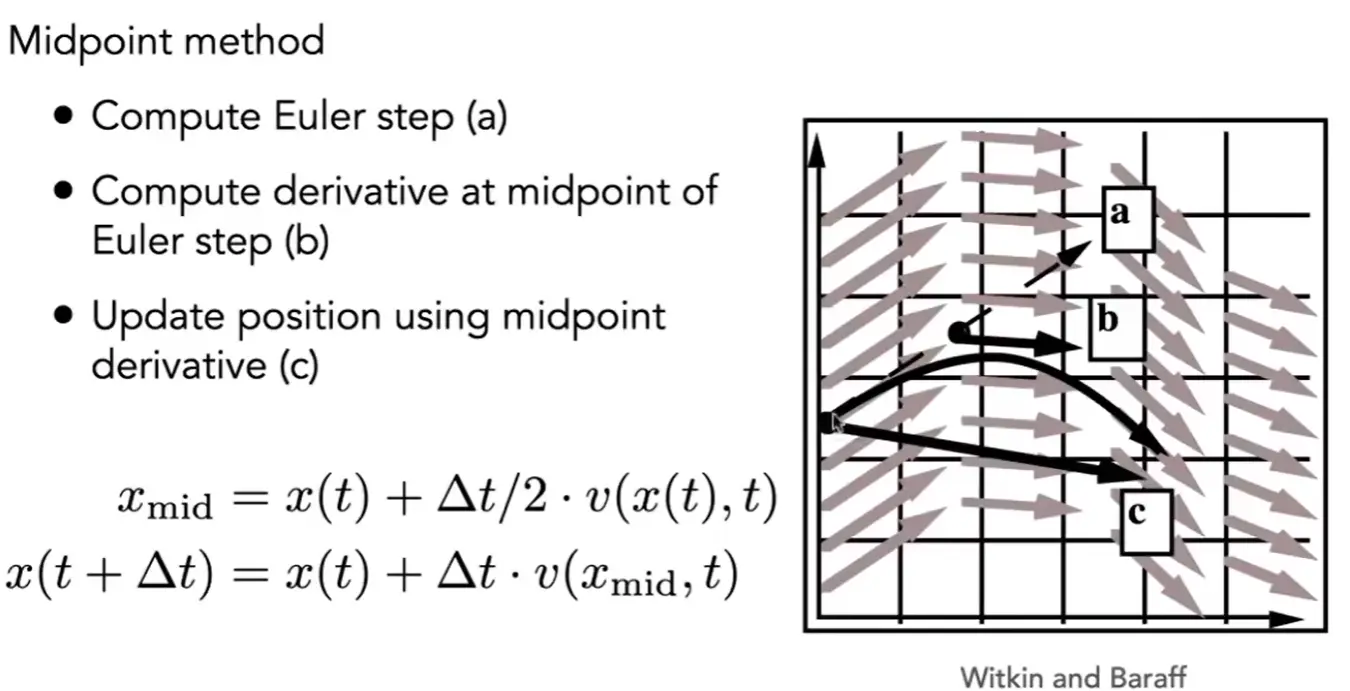
500x256

Note

  1. 计算欧拉方法
  2. 得到欧拉方法下的中点速度
  3. 使用这个中点速度
\[\begin{aligned} x_{\mathrm{mid}} & =x(t)+\Delta t/2\cdot v(x(t),t) \\ x(t+\Delta t) & =x(t)+\Delta t\cdot v(x_{\mathrm{mid}},t) \end{aligned}\]

Modified Euler#

\[\begin{aligned} & \boldsymbol{x}^{t+\Delta t}=\boldsymbol{x}^t+\frac{\Delta t}{2}(\dot{\boldsymbol{x}}^t+\dot{\boldsymbol{x}}^{t+\Delta t}) \\ & \dot{\boldsymbol{x}}^{t+\Delta t}=\dot{\boldsymbol{x}}^t+\Delta t\ddot{\boldsymbol{x}}^t \\ & \boldsymbol{x}^{t+\Delta t}=\boldsymbol{x}^t+\Delta t\dot{\boldsymbol{x}}^t+\frac{(\Delta t)^2}{2}\ddot{\boldsymbol{x}}^t \end{aligned}\]

Note

  • 使用起点和终点处的平均速度
  • 引入二次关系，更加准确

Adaptive Step Size#

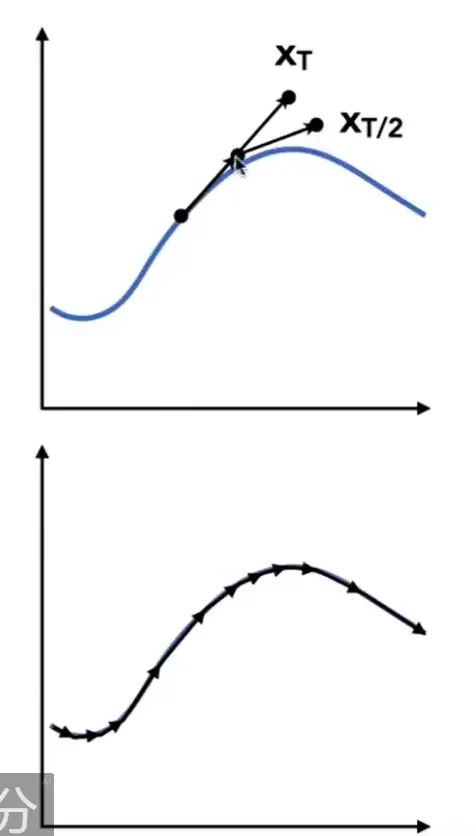
194x338

Note

  • 按照一个步长 \(\Delta t\) 计算得到一个终点
  • 取 \(\Delta t/2\) 计算两次得到另一个终点
  • 每次都取更小的步长，直到得到的终点位置相近

Implicit Euler Method#

\[\begin{aligned} \boldsymbol{x}^{t+\Delta t} & =\boldsymbol{x}^{t}+\Delta t\boldsymbol{\dot{x}}^{t+\Delta t} \\ \boldsymbol{\dot{x}}^{t+\Delta t} & =\boldsymbol{\dot{x}}^{t}+\Delta t\boldsymbol{\ddot{x}}^{t+\Delta t} \end{aligned}\]

Note

  • 直接使用下一时刻的速度加速度
  • 稳定性好，但是需要解方程

quantize "stability"

  • 两种误差定义
    • local truncation error (every step) 局部截断误差
    • total accumulated error (overall) 整体积累误差
  • 假设 \(h=\Delta t\) 表示步长，考虑两种误差的阶（对于隐式欧拉方法）
    • local: \(O(h^2)\)
    • global: \(O(h)\)
  • 如何理解 \(O(h)\)
    • 将步长减小一半，误差也可以减小一半

Runge-Kutta Families - RK4#

a family of advanced methods for solving ODEs, RK4 is a order-four version

500x207

Position-Based / Verlet Intergration#

Note

  • 不完全基于物理

Rigid Body Simulation#

\[\frac{d}{dt} \begin{pmatrix} {\mathrm{X}} \\ {\theta} \\ {\dot{\mathrm{X}}} \\ {\omega} \end{pmatrix}= \begin{pmatrix} {\dot{\mathrm{X}}} \\ {\omega} \\ {\mathrm{F}/M} \\ {\Gamma/I} \end{pmatrix}\]

是对粒子模拟的扩展

Fluid Simulation#

  • 假设用粒子模拟水
  • 假设水是不可压缩的
  • 如果出现了密度不正确的部分，需要修正小球的位置来纠正密度
  • gradient descent 进行局部调整，直到密度不超过阈值

Eulerian vs. Lagrangian#

  • lagrangian: 考虑空间所有的网格
  • eulerian: 考虑很多粒子

Material Point Methods (MPM)#

  • 使用 eulerian 中的粒子来表示物质性质
  • 使用 lagrangian 的网格进行计算
  • 同步更新两种数据结构

Comments