03 Transformation
Why study transformation#
- modeling
- translation
- rotation
- scaling
- viewing
- 3D to 2D projection
2D Transformation#
Scale#
\[\begin{bmatrix}
x^{\prime} \\
y^{\prime}
\end{bmatrix}=
\begin{bmatrix}
s_{x} & 0 \\
0 & s_{y}
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix}\]
- 对角阵
- 可以实现 reflection，例如 \(s_{x}=-1, s_{y}=1\)
Shear#
\[\begin{bmatrix}
x^{\prime} \\
y^{\prime}
\end{bmatrix}=
\begin{bmatrix}
1 & a \\
0 & 1
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix}\]
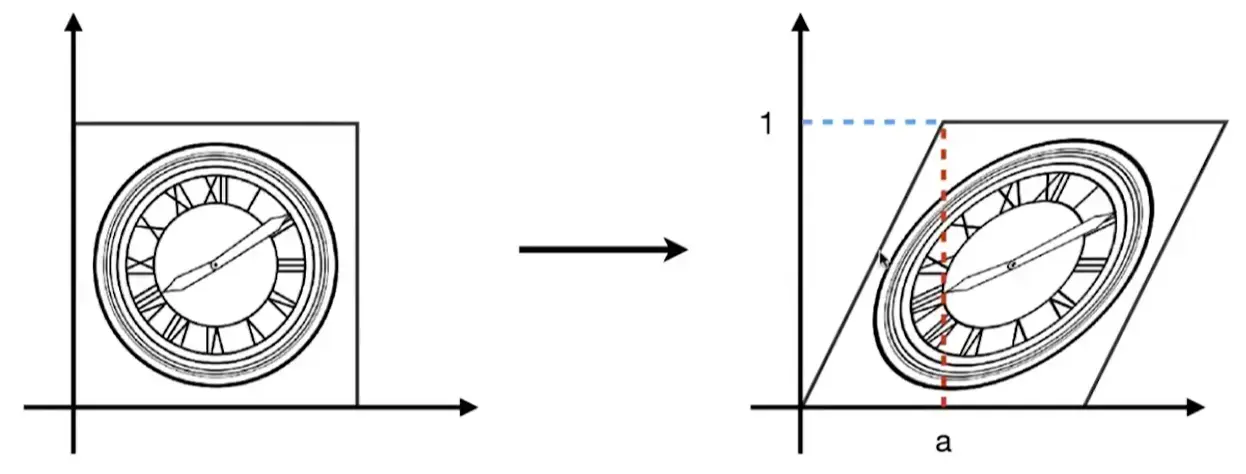
Rotate#
\[\begin{bmatrix}
x^{\prime} \\
y^{\prime}
\end{bmatrix}=
\begin{bmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix}\]
\(\mathbf{R}_{-\theta}=\mathbf{R}_{\theta}^T\)，矩阵的逆等于其转置，称为正交矩阵
Conc: Linear Transformations = Matrices#
\[\begin{bmatrix}
x^{\prime} \\
y^{\prime}
\end{bmatrix}=
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix} \quad \mathbf{x'=M~x}\]
Homogeneous coordinates#
Translation#
Why homogeneous coordinates
\[\begin{bmatrix}
x^{\prime} \\
y^{\prime}
\end{bmatrix}=
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix}+\begin{bmatrix}
t_{x} \\
t_{y}
\end{bmatrix}\]
平移变换中含有常向量，希望使用统一的方式表示变换
- \(w\)-coordinate
- 2D point: \((x,y,1)^T\)
- 2D vector: \((x,y,0)^T\) 向量平移不变性
- 理解
- vec+vec=vec
- point-point=vec
- point+vec=point
\[\begin{pmatrix}
x^{\prime} \\
y^{\prime} \\
w^{\prime}
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & t_x \\
0 & 1 & t_y \\
0 & 0 & 1
\end{pmatrix}\cdot
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}=
\begin{pmatrix}
x+t_x \\
y+t_y \\
1
\end{pmatrix}\]
In homogeneous coordinates, \(\begin{pmatrix}x\\y\\w\end{pmatrix}\) is the 2D point \(\begin{pmatrix}x/w\\y/w\\1\end{pmatrix}\), \(w\neq 0\).
\[\begin{pmatrix}
x^{\prime} \\
y^{\prime} \\
1
\end{pmatrix}=
\begin{pmatrix}
a & b & t_x \\
c & d & t_y \\
0 & 0 & 1
\end{pmatrix}\cdot
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}\]
inverse transform
\(M^{-1}\) 就是逆变换的变换矩阵
Composing Transforms#
- \(T_{(1,0)}\cdot R_{45}\neq R_{45}\cdot T_{(1,0)}\)，旋转默认是绕着原点旋转
- 先旋转再平移比较简单，表示为 \(\mathbf{T} \cdot \mathbf{R}\cdot \mathbf{x}\)
- 变换叠加等价于矩阵乘法，不满足交换律
- \(A_{n}(\ldots A_{2}(A_{1}(\mathbf{x})))=\mathbf{A}_{n}\cdots\mathbf{A}_{2}\cdot\mathbf{A}_{1}\cdot \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}\)
Decomposing Complex Transforms#
- 如何绕任意点 \(\mathbf{c}\) 旋转
- \(\mathbf{T}(\mathbf{c})\cdot \mathbf{R}(\alpha)\cdot \mathbf{T}(-\mathbf{c})\)
3D Transformations#
- 3D point \((x,y,z,1)^T\) 同样能够进行仿射使 \(w=1\)
- 3D vector \((x,y,z,0)^T\)
\[\begin{pmatrix}
x^{\prime} \\
y^{\prime} \\
z^{\prime} \\
1
\end{pmatrix}=
\begin{pmatrix}
a & b & c & t_x \\
d & e & f & t_y \\
g & h & i & t_z \\
0 & 0 & 0 & 1
\end{pmatrix}\cdot
\begin{pmatrix}
x \\
y \\
z \\
1
\end{pmatrix}\]
Summary
一般变换的矩阵表示形式下，先进行线性变换，再进行平移
rotation#
around axis#
\[\begin{gathered}
\mathbf{R}_{x}(\alpha)=
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\alpha & -\sin\alpha & 0 \\
0 & \sin\alpha & \cos\alpha & 0 \\
0 & 0 & 0 & 1
\end{pmatrix} \\
\mathbf{R}_{y}(\alpha)=
\begin{pmatrix}
\cos\alpha & 0 & \sin\alpha & 0 \\
0 & 1 & 0 & 0 \\
-\sin\alpha & 0 & \cos\alpha & 0 \\
0 & 0 & 0 & 1
\end{pmatrix} \\
\mathbf{R}_{z}(\alpha)=
\begin{pmatrix}
\cos\alpha & -\sin\alpha & 0 & 0 \\
\sin\alpha & \cos\alpha & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\end{gathered}\]
- 绕 \(x\) 轴旋转，则 \(x\) 坐标不变
- 其中的 \(\mathbf{R}_{y}\) 的正负号不同，这是因为 \(x \times y=z, y\times z=x\) 但是 \(z\times x=y\)
common#
- 组合绕轴旋转得到任意的 3D rotation: \(\mathbf{R}_{xyz}(\alpha,\beta,\gamma)=\mathbf{R}_x(\alpha)\mathbf{R}_y(\beta)\mathbf{R}_z(\gamma)\)，这里的 \(\alpha,\beta,\gamma\) 称为 Euler angles
- 与飞行模拟中的 roll, pitch, yaw 对应
Rodrigues' Rotation Formula
\[\mathbf{R}(\mathbf{n},\alpha)=\cos(\alpha)\mathbf{I}+(1-\cos(\alpha))\mathbf{n}\mathbf{n}^T+\sin(\alpha)\underbrace{
\begin{pmatrix}
0 & & -n_z & & n_y \\
n_z & & 0 & & -n_x \\
-n_y & & n_x & & 0
\end{pmatrix}}_{\mathbf{N}}\]
表示，绕着 \(\mathbf{n}\) 方向旋转 \(\alpha\) 角
但是上面的公式只能绕着过原点的轴旋转，如果要实现绕着任意轴旋转，如 Decomposing Complex Transforms 将轴上一点平移到原点、旋转并平移回来即可
View/Camera Transformation#
intro#
taking a photo: model -> view -> projection, mvp transformations
define a camera#
- position \(\vec{e}\)
- gaze direction \(\hat{g}\)
- up direction \(\hat{t}\) 画面的向上方向
Key observation
如果相机和其他物体相对静止，那么看到的结果是一样的，因此可以将相机放在标准位置上
- \(\vec{e}=\vec{0}\)
- \(\hat{g}=-Z\)
- \(\hat{t}=Y\)
这样能有利于操作简化，但也会带来问题
transform camera to standard pos#
- 基本思想
- 将相机移动到原点
- 将 g 转到 -Z
- 将 t 转到 Y
- \(M_{\text{view}}=R_{\text{view}}\cdot T_{\text{view}}\)
- \(T_{\text{view}}= \begin{bmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix}\)
- \(R_{\text{view}}\)?
如何求 \(R_{\text{view}}\)
从逆变换出发，先求出 \(Y\to t, g\to -Z, (g\times t)\to X\)
\[R_{\text{view}}^{-1}=
\begin{bmatrix}
x_{\hat{g}\times\hat{t}} & x_t & x_{-g} & 0 \\
y_{\hat{g}\times\hat{t}} & y_t & y_{-g} & 0 \\
z_{\hat{g}\times\hat{t}} & z_t & z_{-g} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}\]
然后进行转置就能得到
\[R_{\text{view}}=
\begin{bmatrix}
x_{\hat{g}\times\hat{t}} & y_{\hat{g}\times\hat{t}} & z_{\hat{g}\times\hat{t}} & 0 \\
x_t & y_t & z_t & 0 \\
x_{-g} & y_{-g} & z_{-g} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}\]
Conc.#
- 物体和相机进行相同的变换
- 相机变换到标准位置
- 然后就能处理投影了
Projection Transformation#
- 3D to 2D
- Orthographic projection 正交投影
- Perspective projection 透视投影
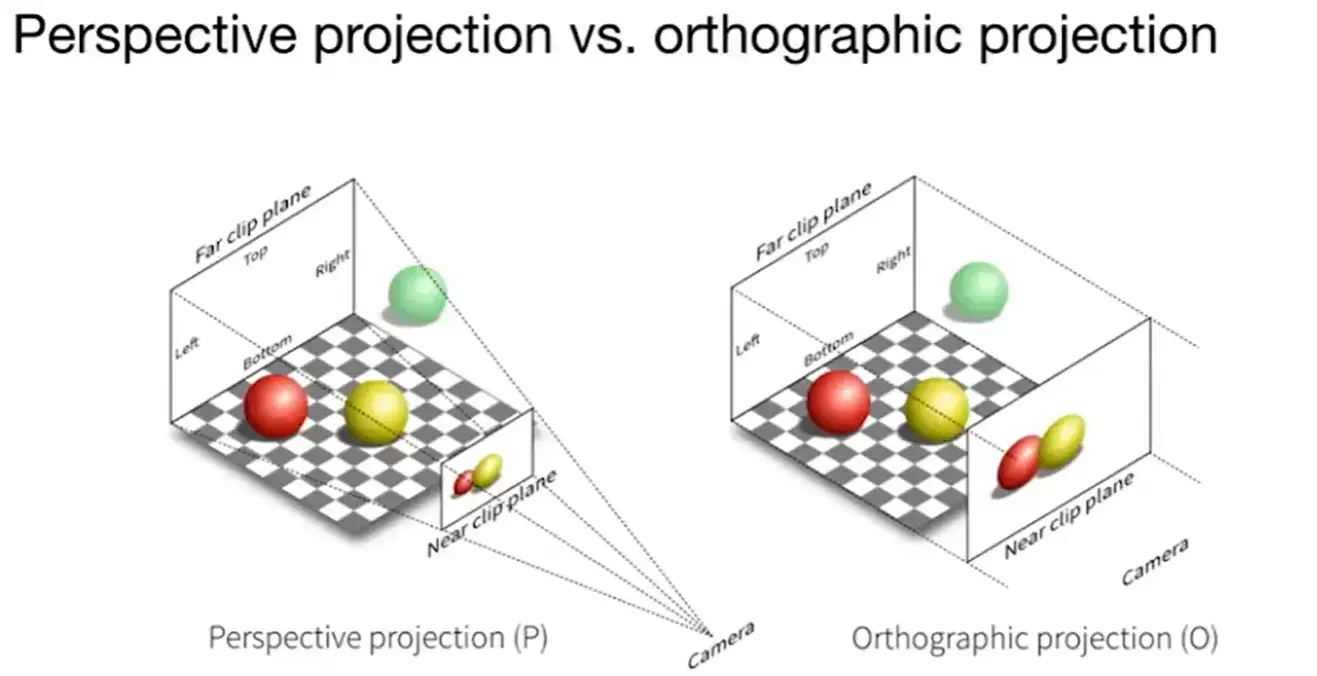
Orthographic Projection#
simple way#
- 相机在原点，朝向 -Z，向上 Y
- 扔掉 Z 坐标 先不考虑物体的遮挡
- 将所有的内容移动和缩放到 \([-1,1]^2\)，方便后续计算
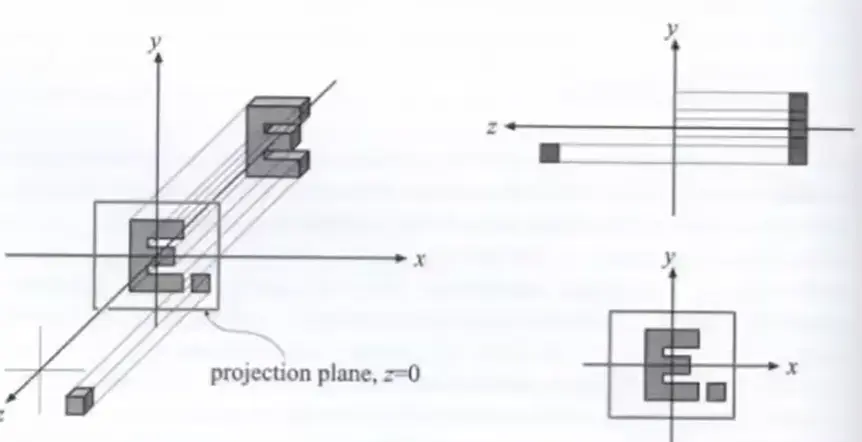
in general#
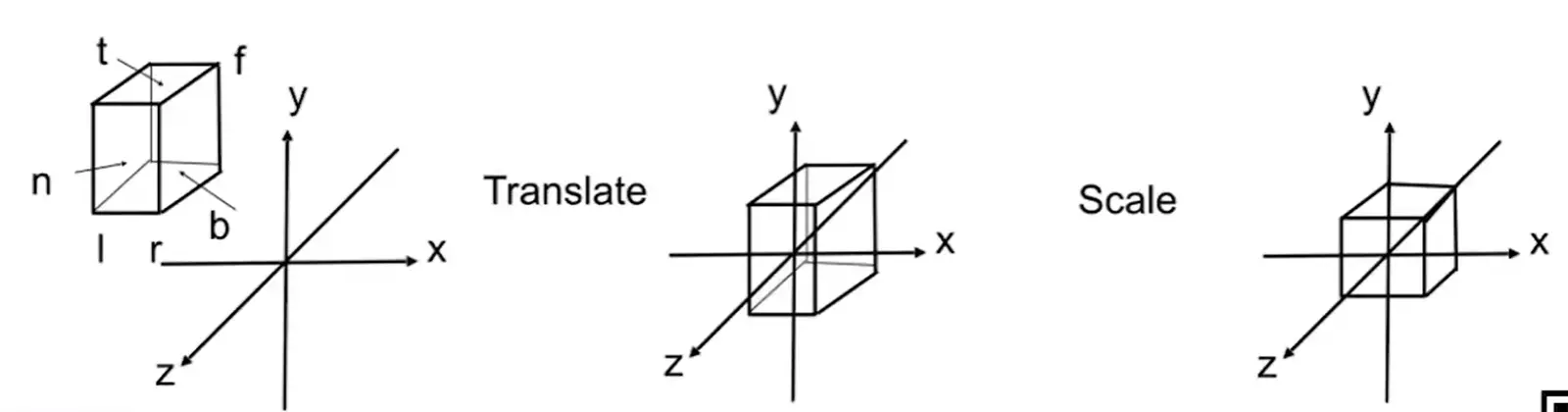
- 将空间中任意一个立方体 (Cuboid) \([l,r]\times[b,t]\times[f,n]\) 映射到标准立方体 \([-1,1]^3\)，注意右手系中 Z 越大表示距离相机越近
- 先平移，中心点移到原点
- 再缩放
\[M_{ortho}=
\begin{bmatrix}
\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{n-f} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & -\frac{r+l}{2} \\
0 & 1 & 0 & -\frac{t+b}{2} \\
0 & 0 & 1 & -\frac{n+f}{2} \\
0 & 0 & 0 & 1
\end{bmatrix}\]
Note
OpenGL 之类的 API 使用的是左手系，Z 越大表示离相机越远
Perspective Projection#
平行线不再平行了 例如铁轨相交
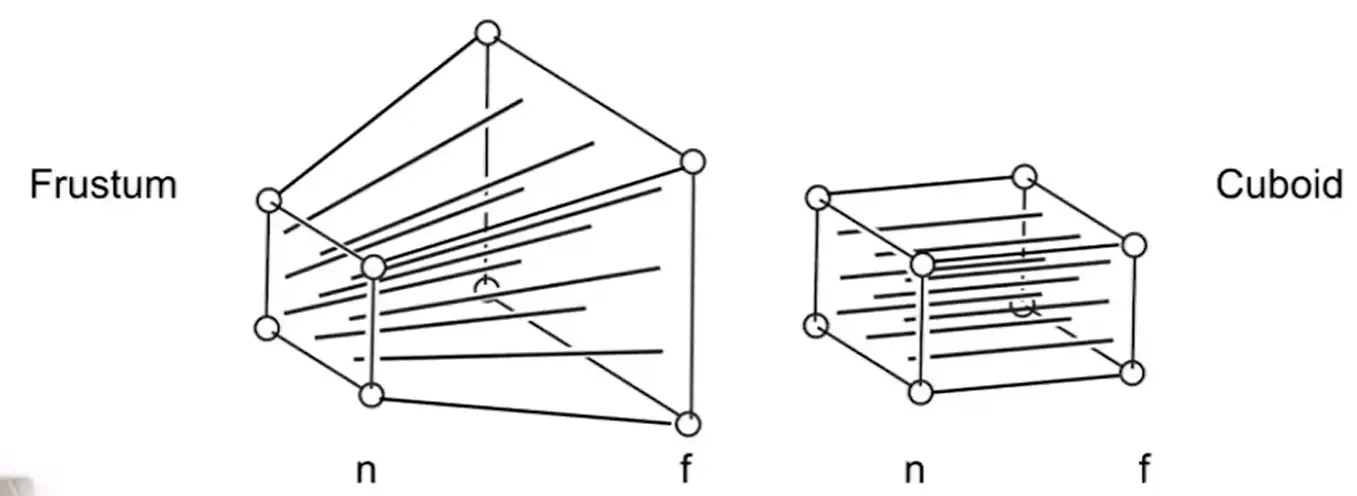
- 将 Frustum 压成一个 Cuboid
- 然后进行正交投影
squish#
- 规定 n 平面不变
- 规定 f 平面 Z 不变
- 规定 f 平面中心点不变
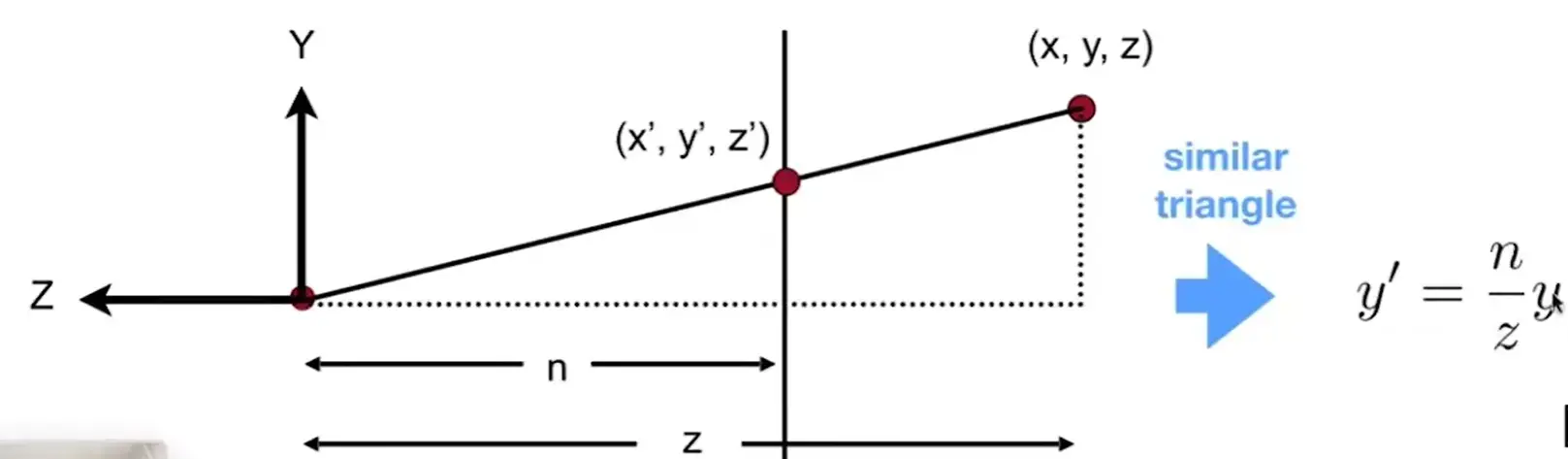
in homogeneous coordinates#
\[\begin{pmatrix}
x \\
y \\
z \\
1
\end{pmatrix}\Rightarrow
\begin{pmatrix}
nx/z \\
ny/z \\
\mathrm{unknown} \\
1
\end{pmatrix}\overset{\text{mult. by z}}{\operatorname*{==}}
\begin{pmatrix}
nx \\
ny \\
\text{still unknown} \\
z
\end{pmatrix}\]
所以根据 \(M_{persp\to ortho}^{(4\times4)} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}= \begin{pmatrix} nx \\ ny \\ \mathrm{unknown} \\ z \end{pmatrix}\)，已经可以推导出部分矩阵：
\[M_{persp\to ortho}=
\begin{pmatrix}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
? & ? & ? & ? \\
0 & 0 & 1 & 0
\end{pmatrix}\]
由于 n 平面上的点不会发生变化：
\[\begin{pmatrix}
x \\
y \\
n \\
1
\end{pmatrix}\Rightarrow
\begin{pmatrix}
x \\
y \\
n \\
1
\end{pmatrix}==
\begin{pmatrix}
nx \\
ny \\
n^2 \\
n
\end{pmatrix}\]
第三行结果与 \(x,y\) 都没有关系，所以可能是 \((0,0,A,B)\)，那么：
\[
\begin{pmatrix}
0 & 0&A&B
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
n \\
1
\end{pmatrix}=An+B=n^2
\]
同理，f 平面上的点 Z 也不变，有 \(Af+B=f^2\)，联立得到 \(\begin{cases}A=n+f \\ B=-nf\end{cases}\)
所以：
\[M_{persp\to ortho}=
\begin{pmatrix}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0
\end{pmatrix}\]
且 \(M_{persp}=M_{ortho}M_{persp\to ortho}\)
经过变换后，中间的点的 Z 值如何变化？
变换后，\(z'=\frac{z(n+f)-nf}{z}=n+f-\frac{nf}{z}>z\)，所以是变近了