05 Shading

intro

Shading, noun, The darkening or coloring of an illustration or diagram with parallel lines or a block of color. In this course, the process of applying a material to an object.

A Simple Shading Model (Blinn-Phong Reflectance Model)

• specular highlights 高光（镜面反射）
• diffuse reflection 颜色渐变（漫反射）
• ambient lighting 间接光照

the model

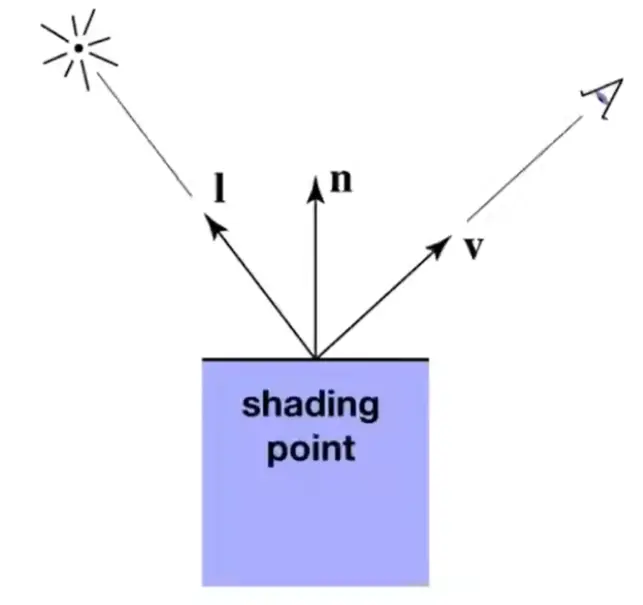
• viewer direction, \(\hat{v}\)
• surface normal, \(\hat{n}\)
• light direction, \(\hat{l}\)
• surface parameters: color, shiness, ...

shading is local

shading 并没有考虑光线的遮挡关系，不会画出阴影 shading \(\neq\) shadow

Diffuse Refelction

光线向着所有方向均匀反射

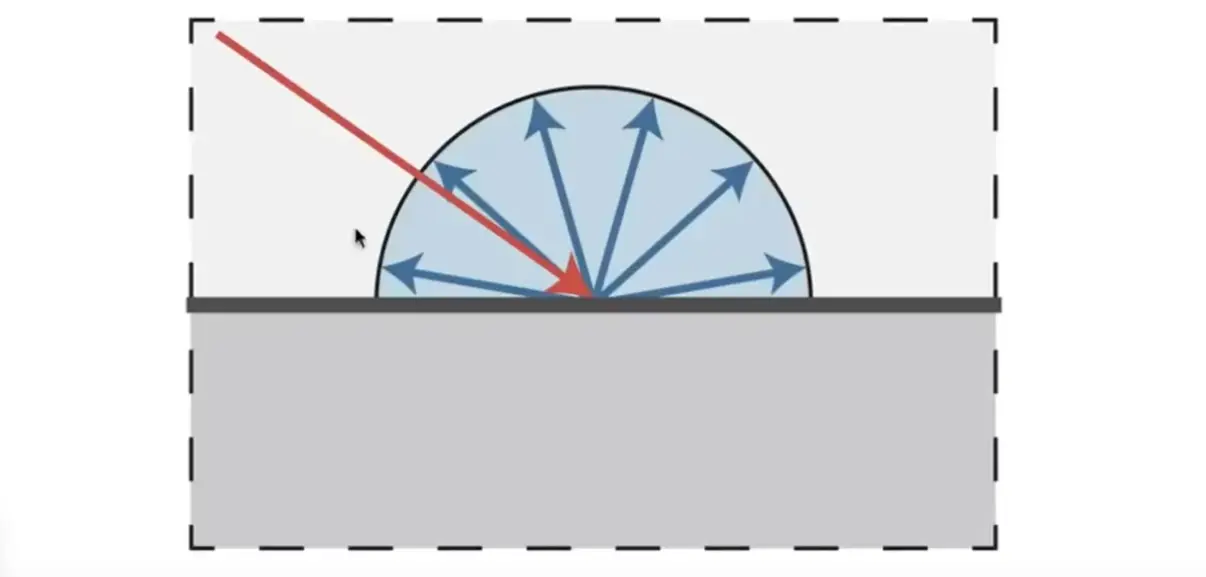
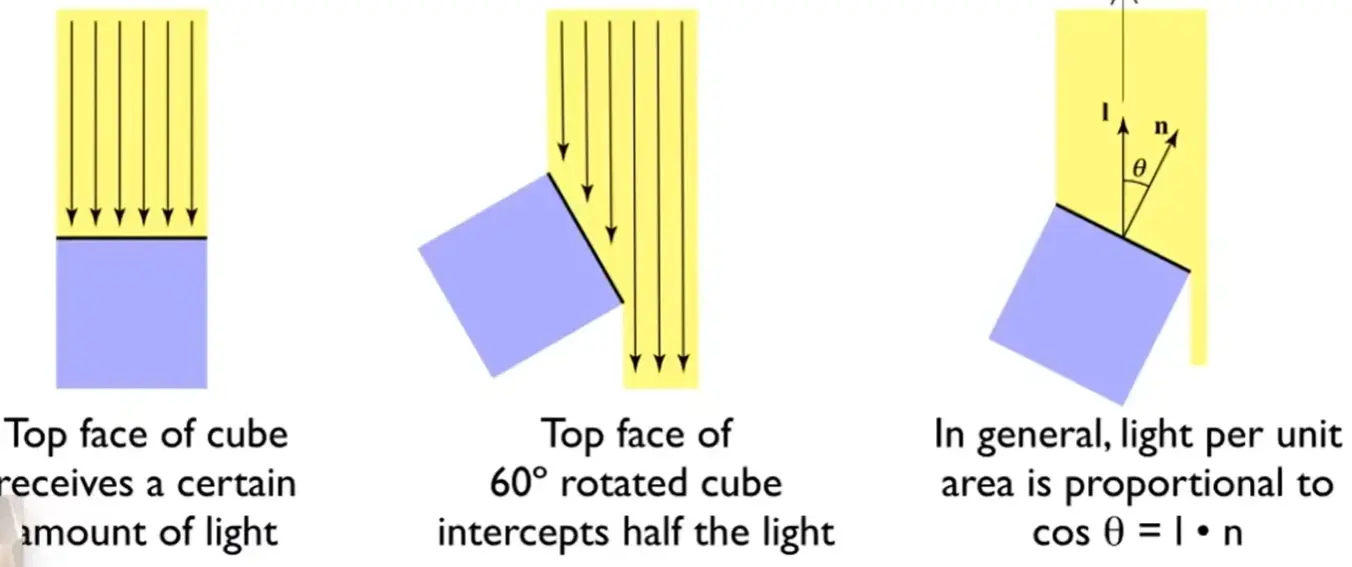
Note

• 平行光情景下，单位面积接收光强与 \(\cos \theta=\hat{l}\cdot \hat{n}\) 成正比
• 点光源情境下，单位面积接收光强与 \(r^2\) 成反比

Lambertian (Diffuse) Shading:

\[L_{d}=k_{d}(I/r^2) \max(0,\hat{n}\cdot \hat{l})\]

• \(k_{d}\) diffuse coeffficient，与表面性质、波长有关
• \(r\) 是光源与 shading point 的距离

Specular Term

birght near mirror reflection direction

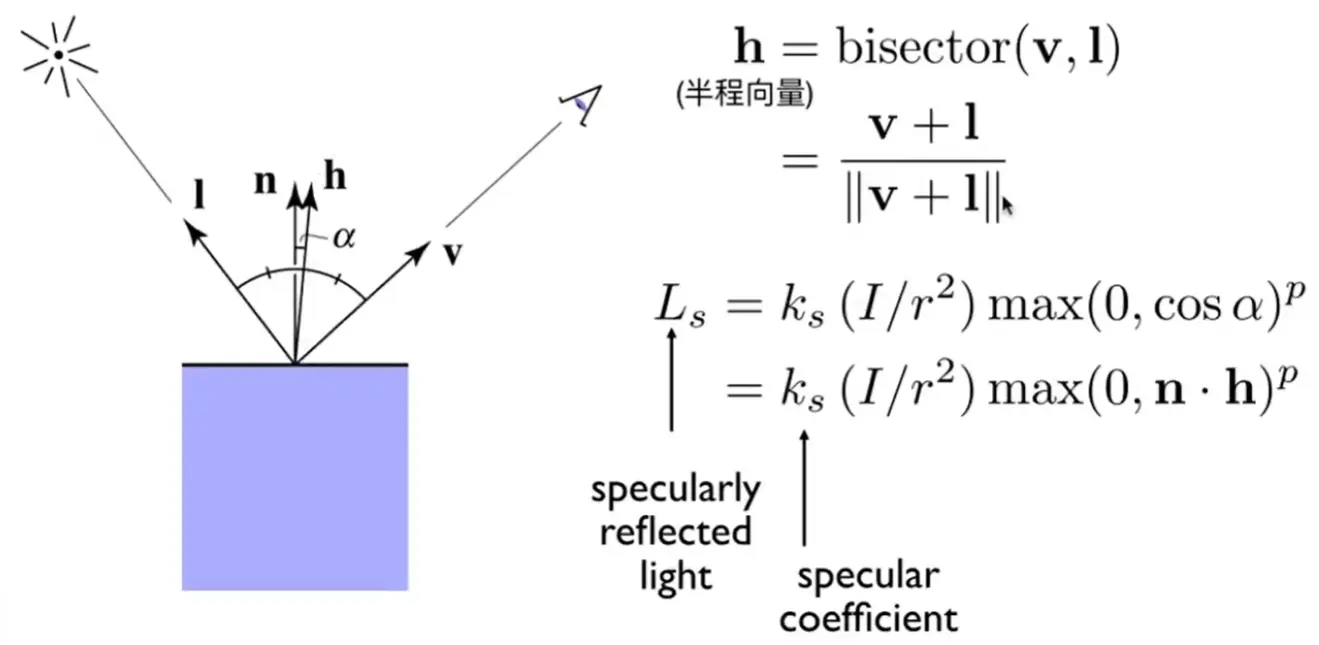
bisector vector \(h\):

\[\mathbf{h}=\text{bisector}(\mathbf{v},\mathbf{l})=\frac{\mathbf{v}+\mathbf{l}}{||\mathbf{v}+\mathbf{l}||}\]

\[L_{s}=k_{s}(I/r^2)\max(0,\mathbf{n}\cdot\mathbf{h})^p\]

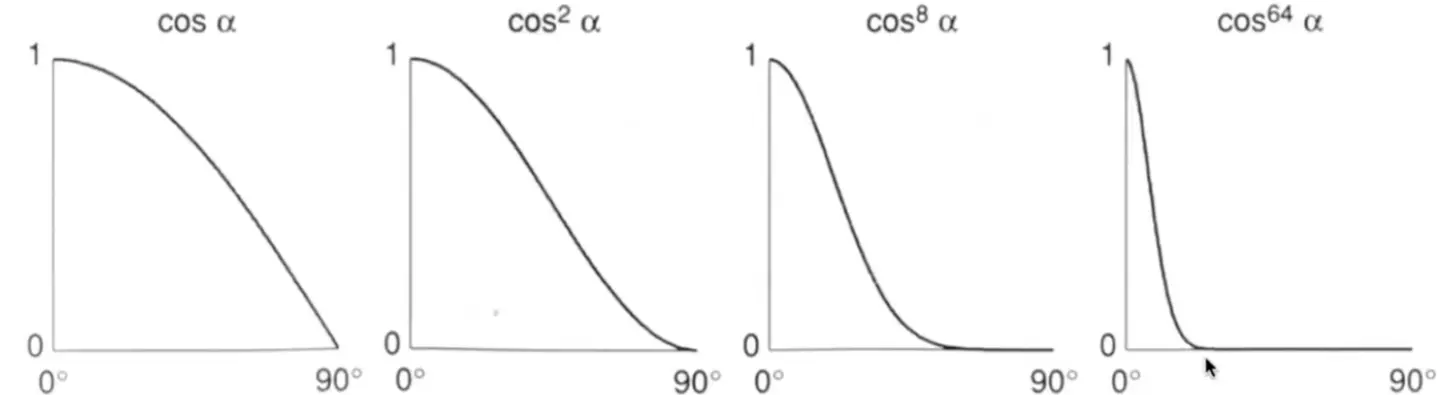
其中指数 \(p\) 有利于控制镜面反射范围，一般取 100~200

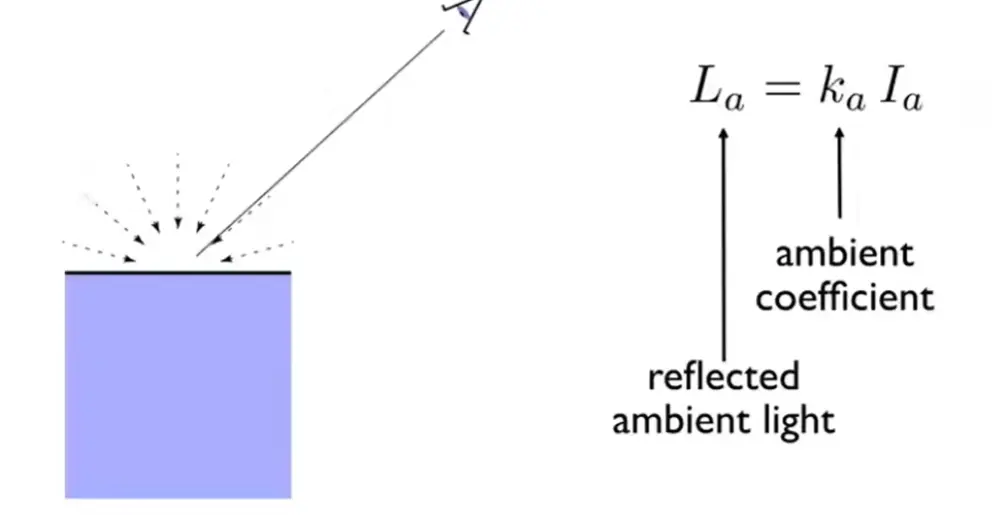
Ambient Term

假设环境光强为定值 \(I_{a}\)

\[L_{a}=k_{a}I_{a}\]

Conclusion

\[\begin{aligned} \mathrm{L} & =L_a+L_d+L_s \\ & =k_aI_a+k_d(I/r^2)\max(0,\mathbf{n}\cdot\mathbf{l})+k_s(I/r^2)\max(0,\mathbf{n}\cdot\mathbf{h})^p \end{aligned}\]

Note

并不考虑 viewer 距离对亮度的影响

Shading Frequencies

上图中分别是平面着色(Flat shading)、顶点着色再插值(Gouraud shading)和像素着色(Phong shading)

Note

模型面数足够多时，Flat 也可能和 Phong 一样好

per-vertex normal vectors

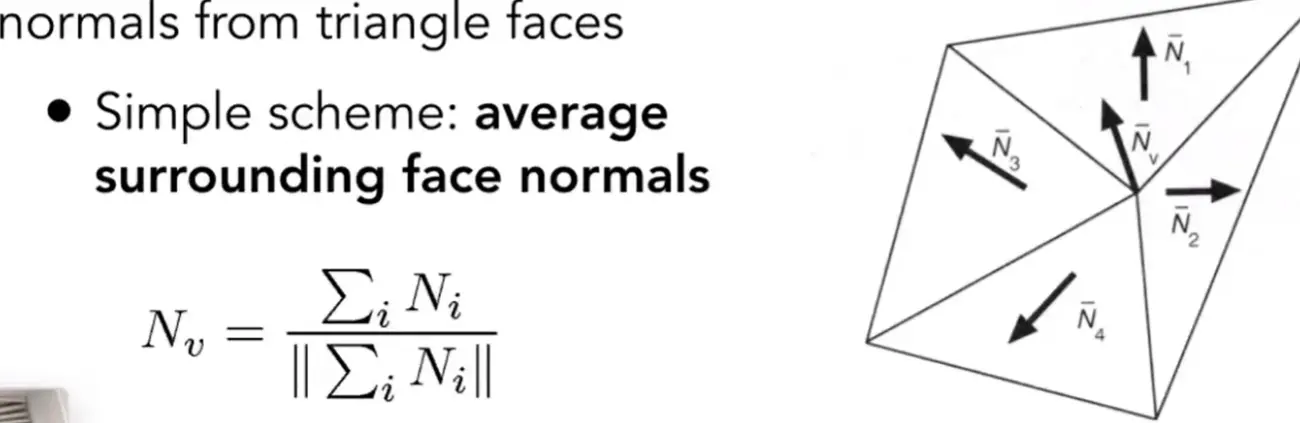
Note

可以平均，也可以加权平均

per-vertex normal vectors

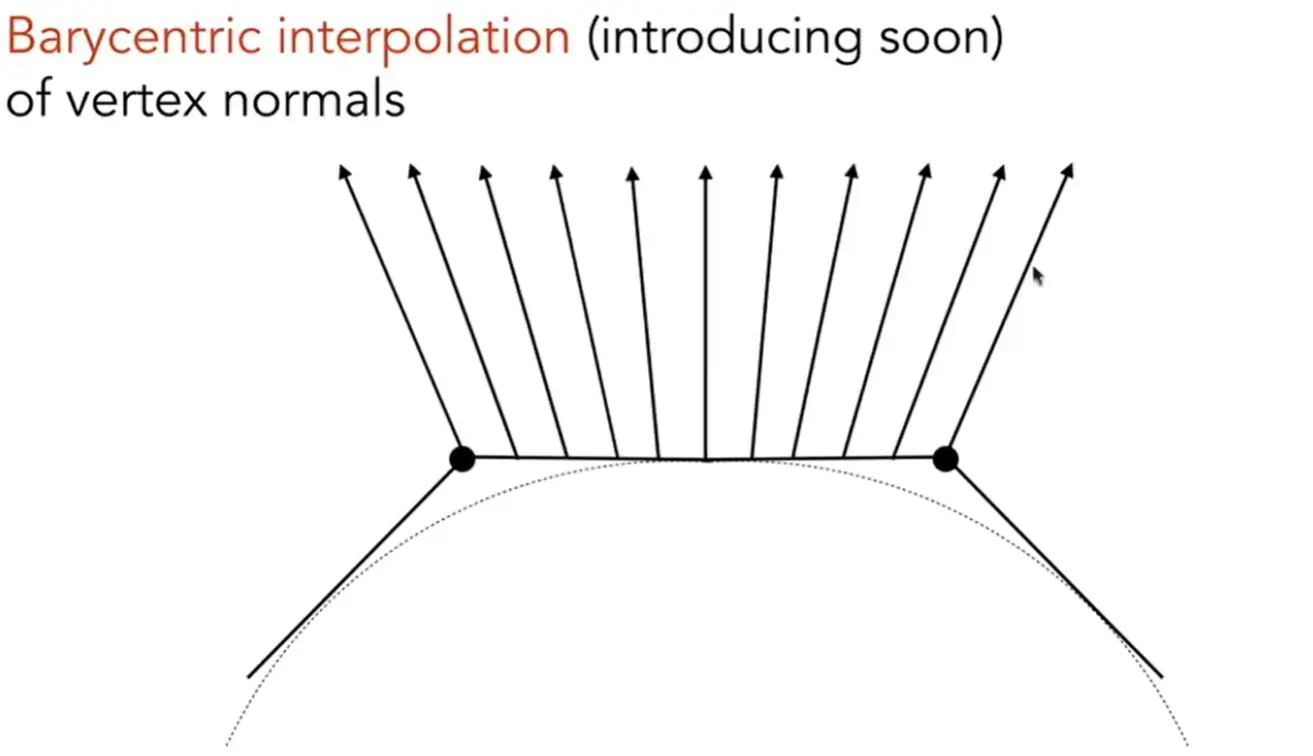
Note

使用重心坐标插值方法

Graphics (Real-time Rendering) Pipeline

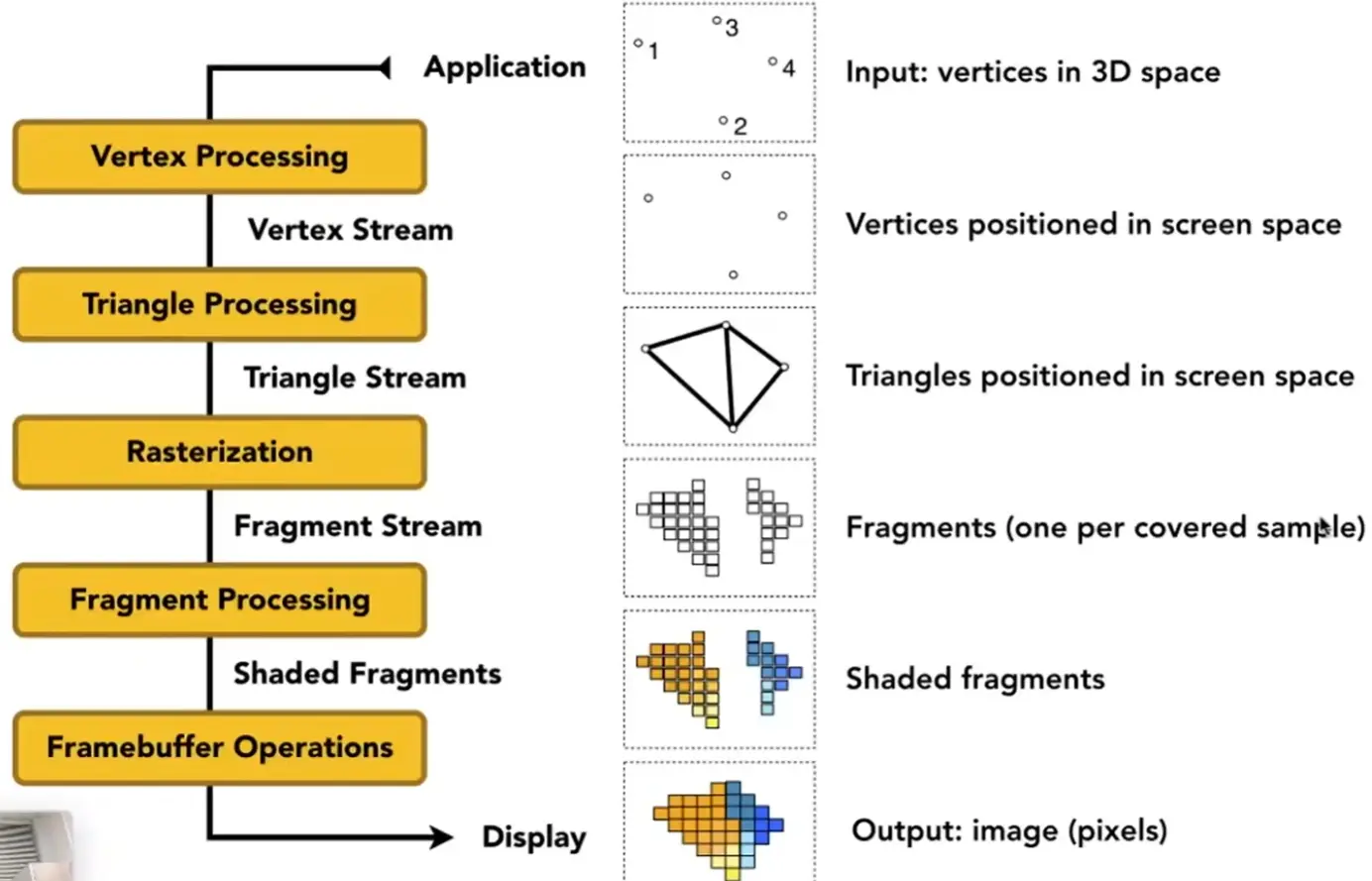
Shader Programs

uniform sampler2D myTexture;                      // program param
uniform vec3 lightDir;                            // program param
varying vec2 uv;                                  // per fragment value (interp. by rasterizer)
varying vec3 norm;                                // per fragment value (interp. by rasterizer)

void diffuseShader() {
    vec3 kd;
    kd = texture2d(myTexture, uv);                // material color from texture
    kd *= clamp(dot(-lightDir, norm), 0.0, 1.0);  // Lambertian shading model
    gl_FragColor = vec4(kd, 1.0);                 // output fragment color
}

Shadertoy BETA

Goal: highly complex 3D scenes in realtime

Texture Mapping

在物体不同位置定义不同的属性

Note

• 制作纹理时，需要实现三维模型尽可能简单地展开成平面纹理，扭曲越小越好
• 渲染时，需要实现纹理三角形到模型三角形的映射

Texture Coordinates

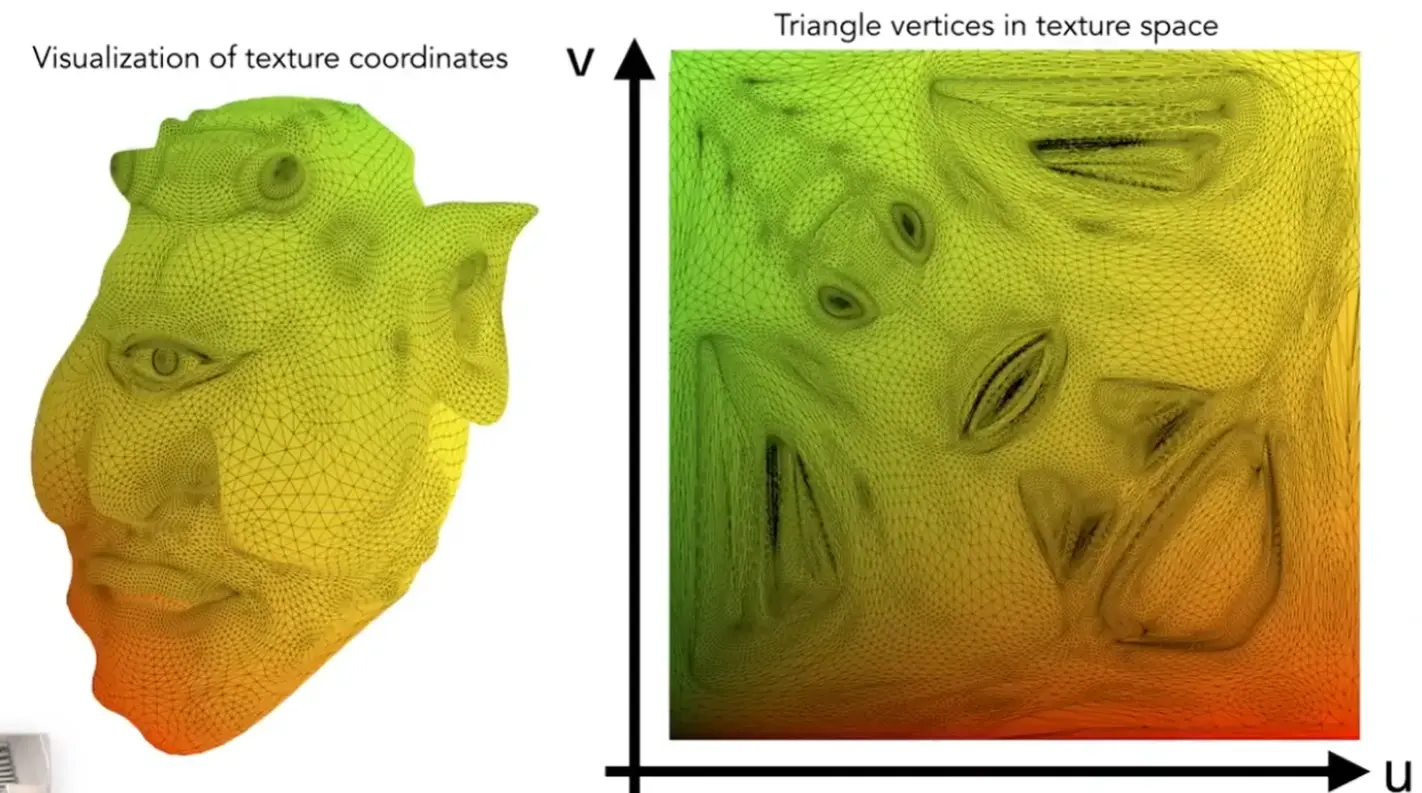
Note

• 约定 \(u,v\in[0,1]\)
• 模型上每个三角形的顶点都在纹理图上有一个 \((u,v)\) 映射
• 三角形内部的点用插值计算

Simple Texture Mapping: Diffuse Color

for each rasterized screen sample(x, y):
    (u, v) = evaluate texture coordinate at (x, y)
    texcolor = texture.sample(u, v);
    set sample's color to texcolor;

what if the texture is too small?

• texel 纹理元素，纹素
• 一个 pixel 会映射到文理上的一个坐标，不一定能刚好到一个 texel，如果直接四舍五入会导致分辨率不高
  • 需要进行插值

Bilinear Interpolation

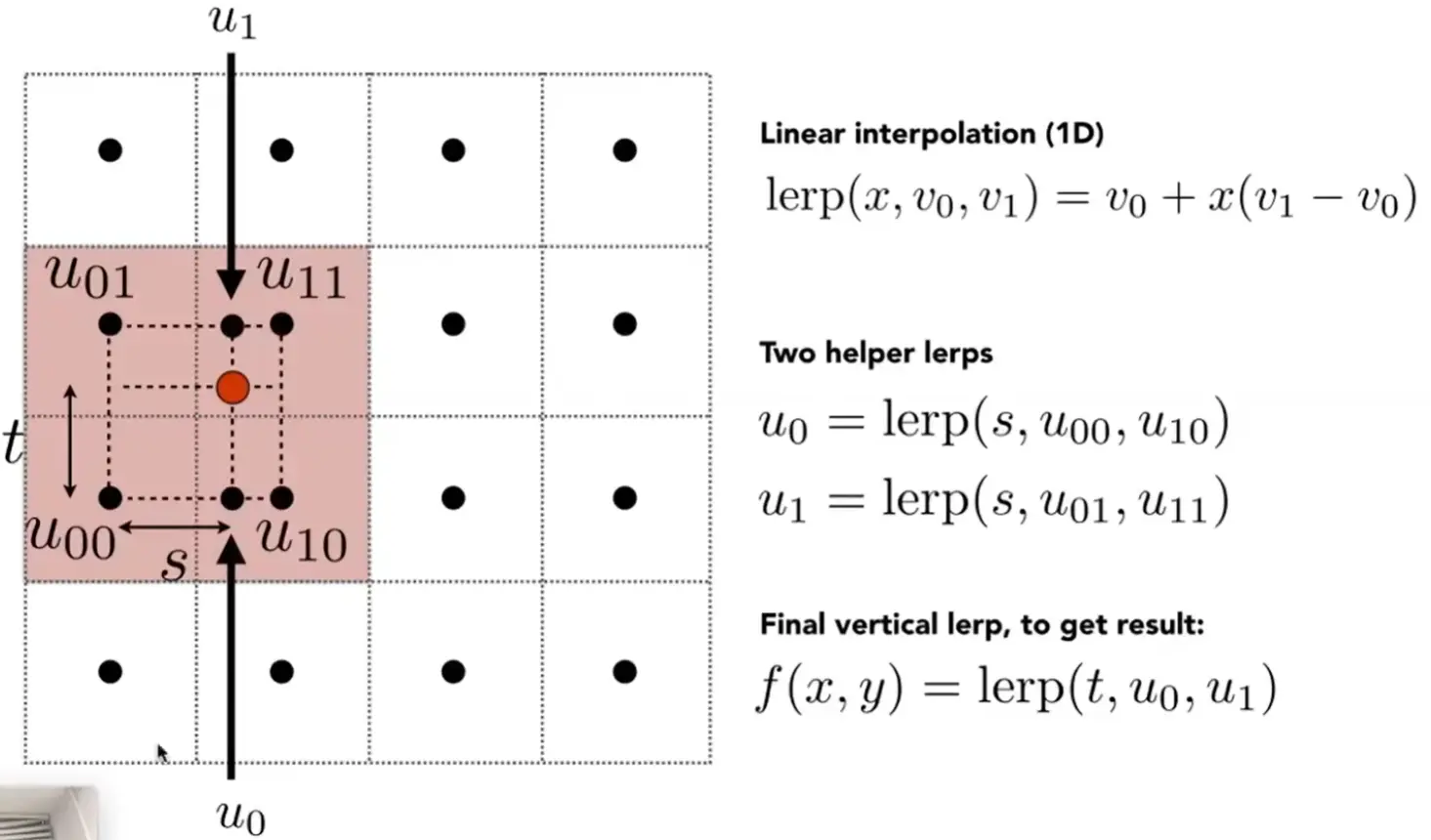
Bicubic Interpolation

• 取了周围十六个
• 进行三次插值

what if the texture is too big?

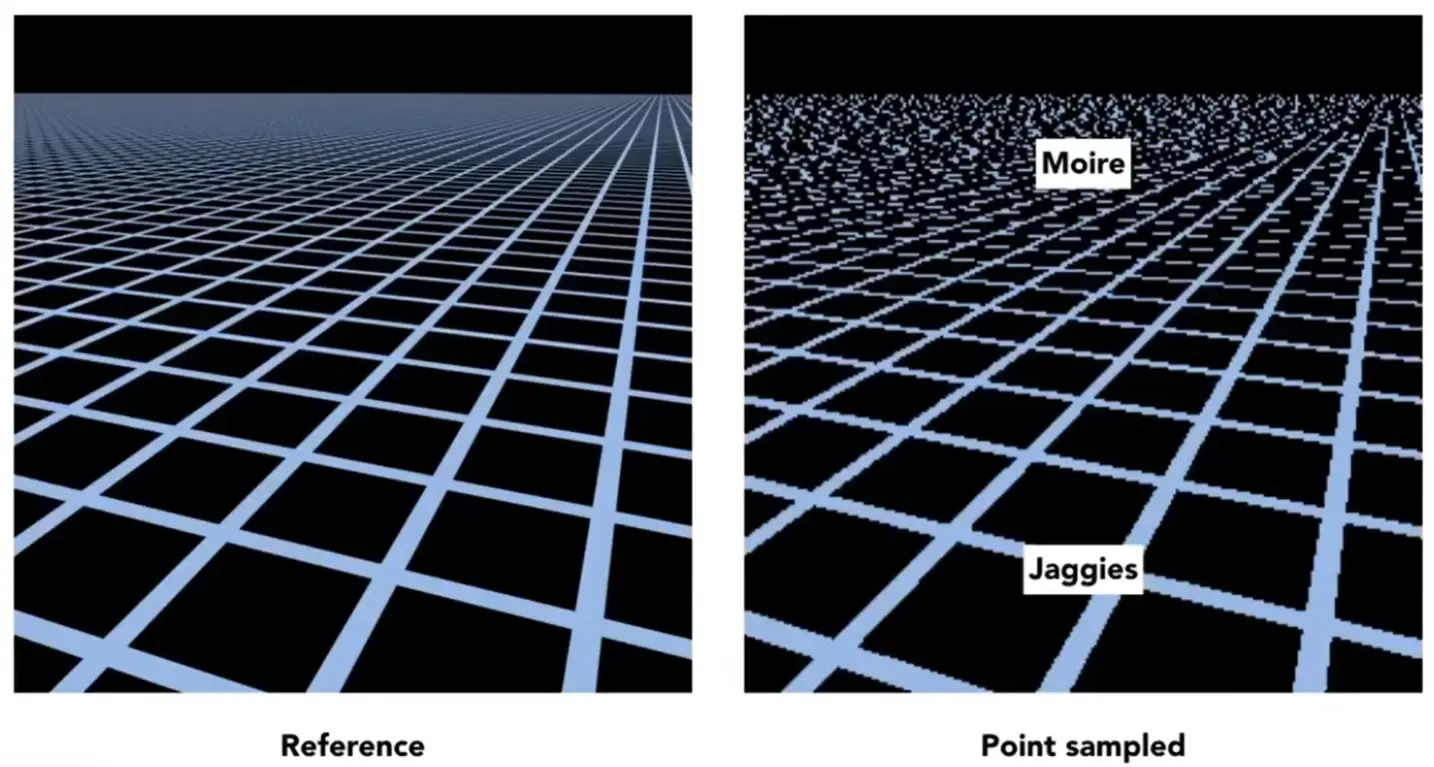
联系前面的走样问题 GAMES101 04 Rasterization#Antialiasing

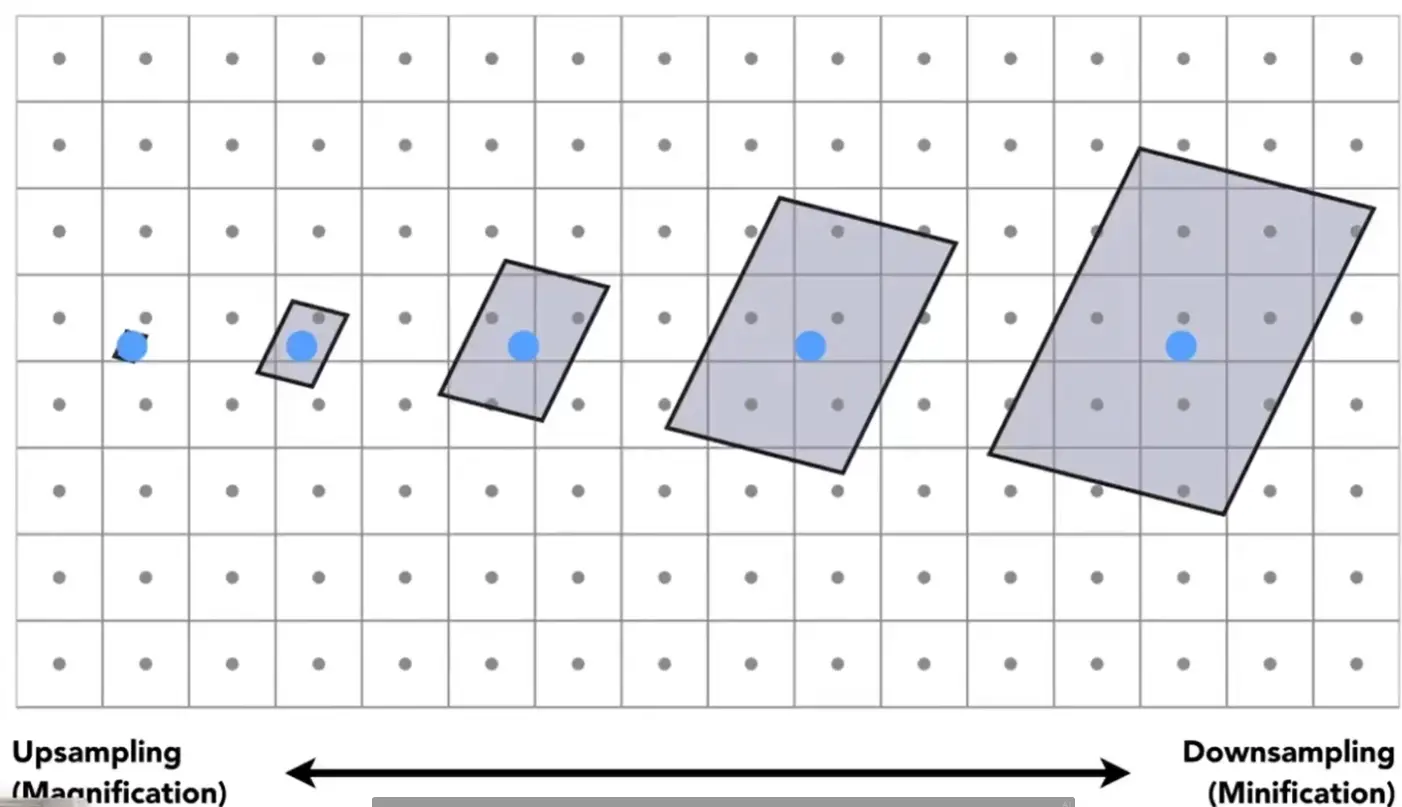
Note

在远处，一个像素覆盖的纹理区域大小非常大，但也是用像素重心采样，导致失真

supersampling?

• 一个像素内有高频的信息，于是使用超采样的方法，一定能解决
• 但是会导致效率很低

Mipmap

intro

range query: 给定一个区域，快速得到区域的平均值 Mipmap: allowing (fast, approx., square) range query

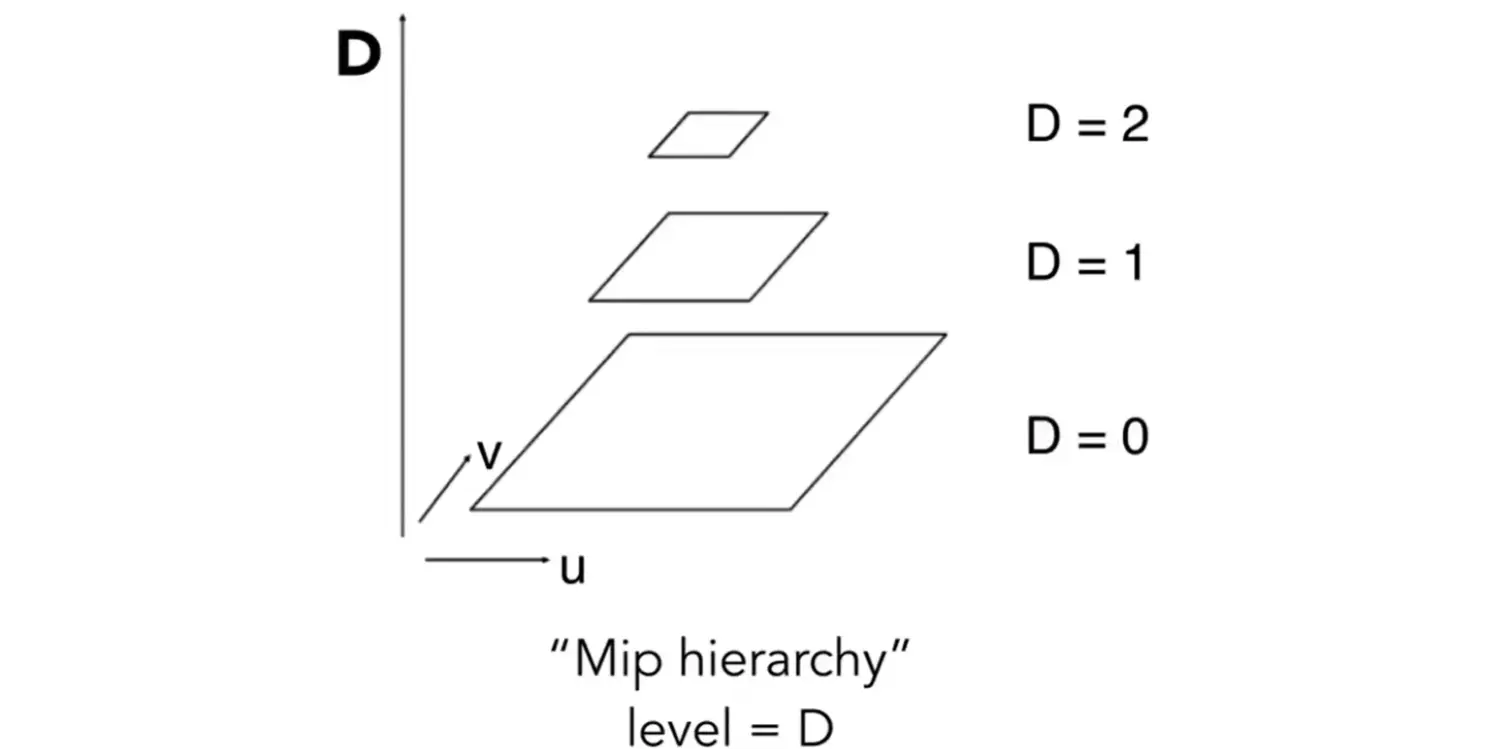
• \(O(\log n)\) levels
• \(O(\frac{4}{3}n)\) space

step 1: pixel to texels

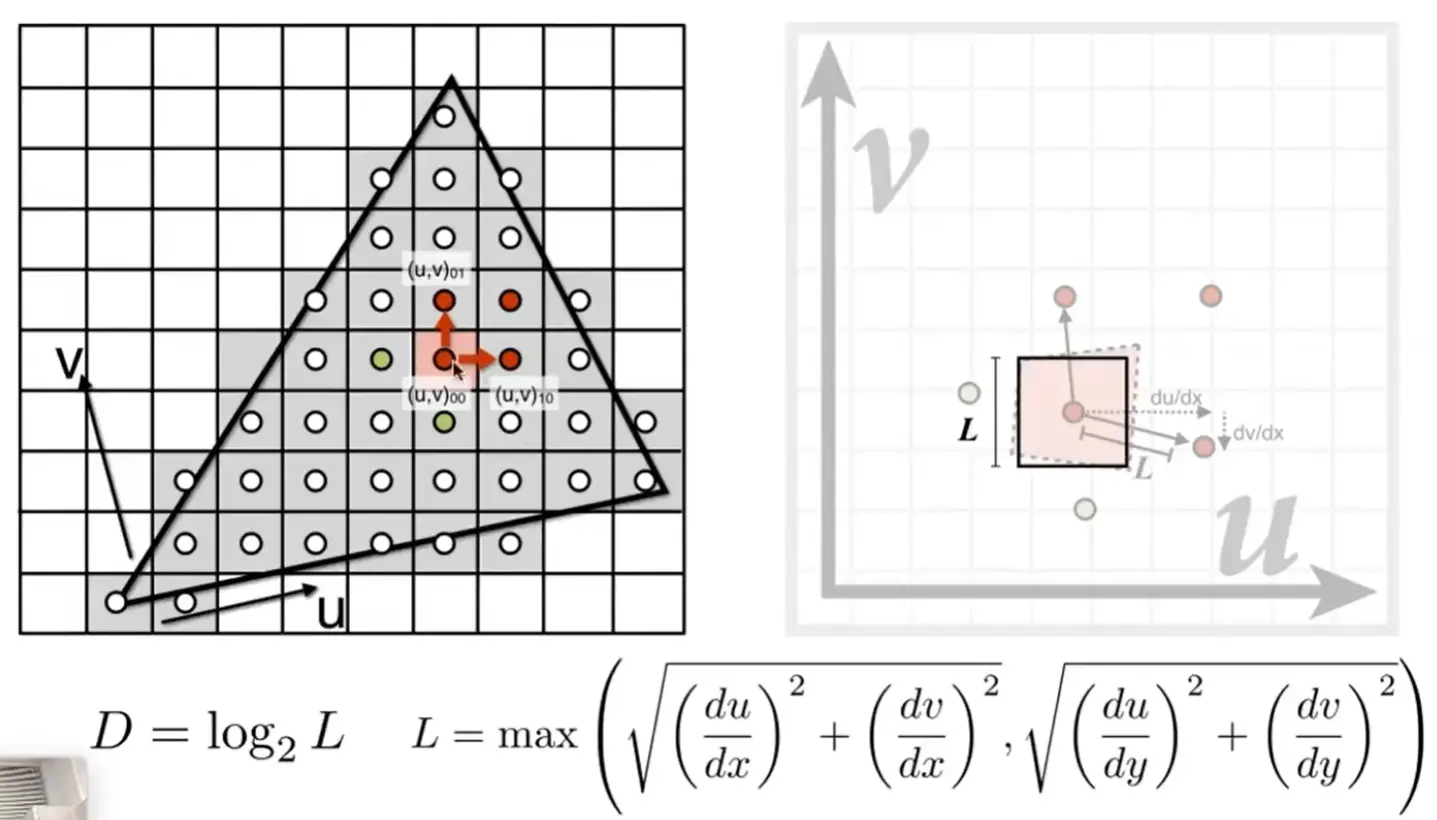
1. 对于需要渲染的像素，将其和其四个邻居都映射到纹理图上，得到对应坐标
2. 找到纹理上距离到最远邻居的距离 \(L\)
3. 将 texel 区域近似为边长为 \(L\) 的正方形区域

step 2: use mipmap

1. 在 \(D=\log_{2}L\) 层，这个正方形区域的大小正好是一个像素，在这一层进行查找
2. 进行双线性插值

step 3: trilinear interpolation

Note

• 上图中，距离近的位置 \(D\) 很大，需要在很深的层去查询
• 存在边缘，会导致不连续
• 需要让 \(D\) 是小数时的变化连续

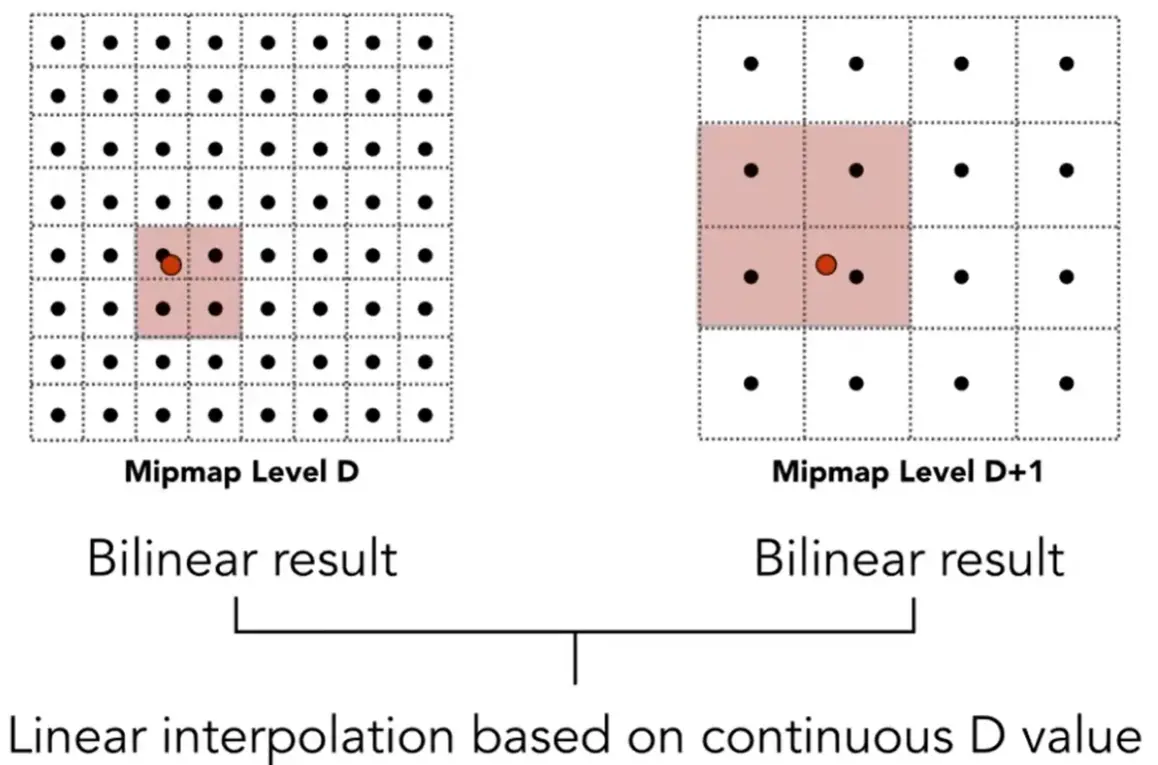
在层间进行第三次插值

Anisotropic Filtering

各向异性过滤

mipmap limitations

overblur，远处的细节都糊掉了，原因是近似成正方形差的太多了，例如当 texels 是一个很长的矩形时

Note

• mipmap 只是预计算了对角线上的
• 各向异性过滤预计算了不同比例矩形的小图，\(O(4n)\) space

EWA Filtering

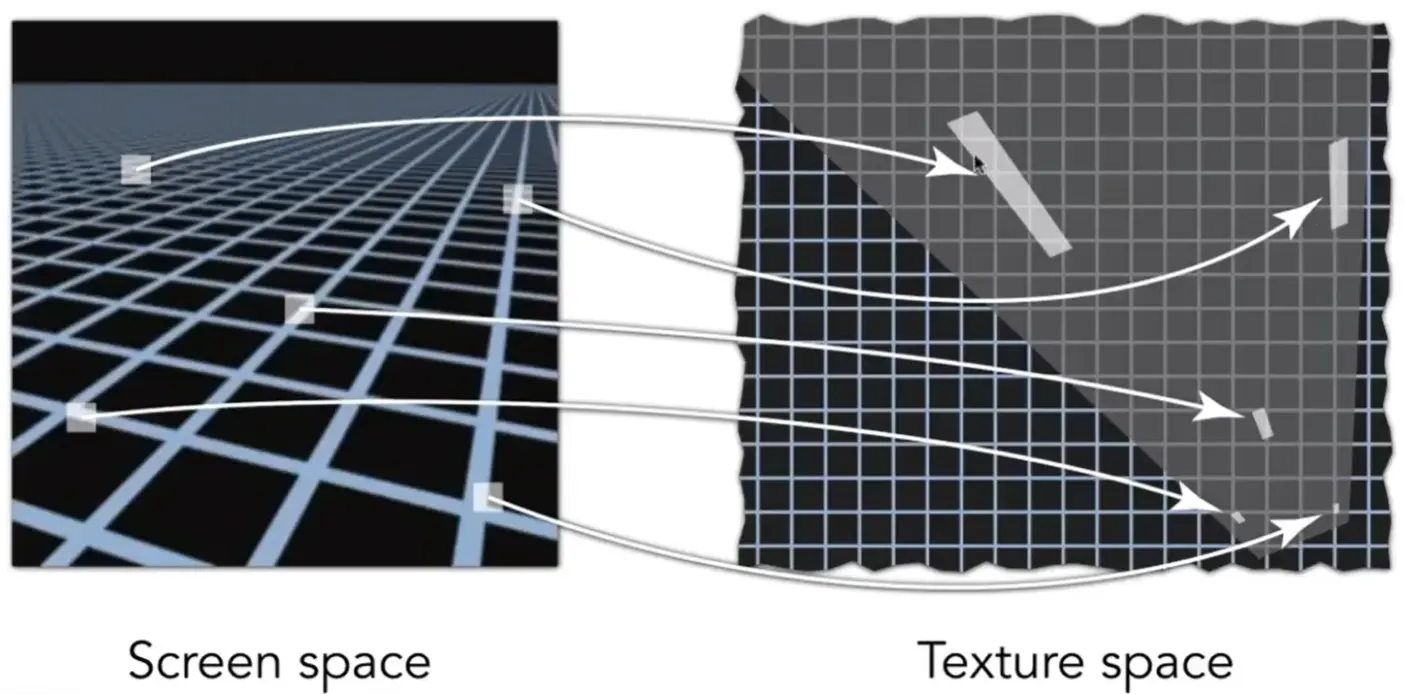
Note

同理，各向异性过滤无法处理矩形斜着的问题

• use multiple lookups
• weighted average
• mipmap hierarchy still helps
• can handle irregular footprints

Application of Textures

纹理不一定需要是图像，也可以是其他属性

Environment map

• 可以用一个球来记录整个环境光
  • 展开之后会有变形类比世界地图
• 用外接立方体来记录环境光，变形比较小

Bump mapping

• 凹凸贴图，在模型不变的情况下改变法向量

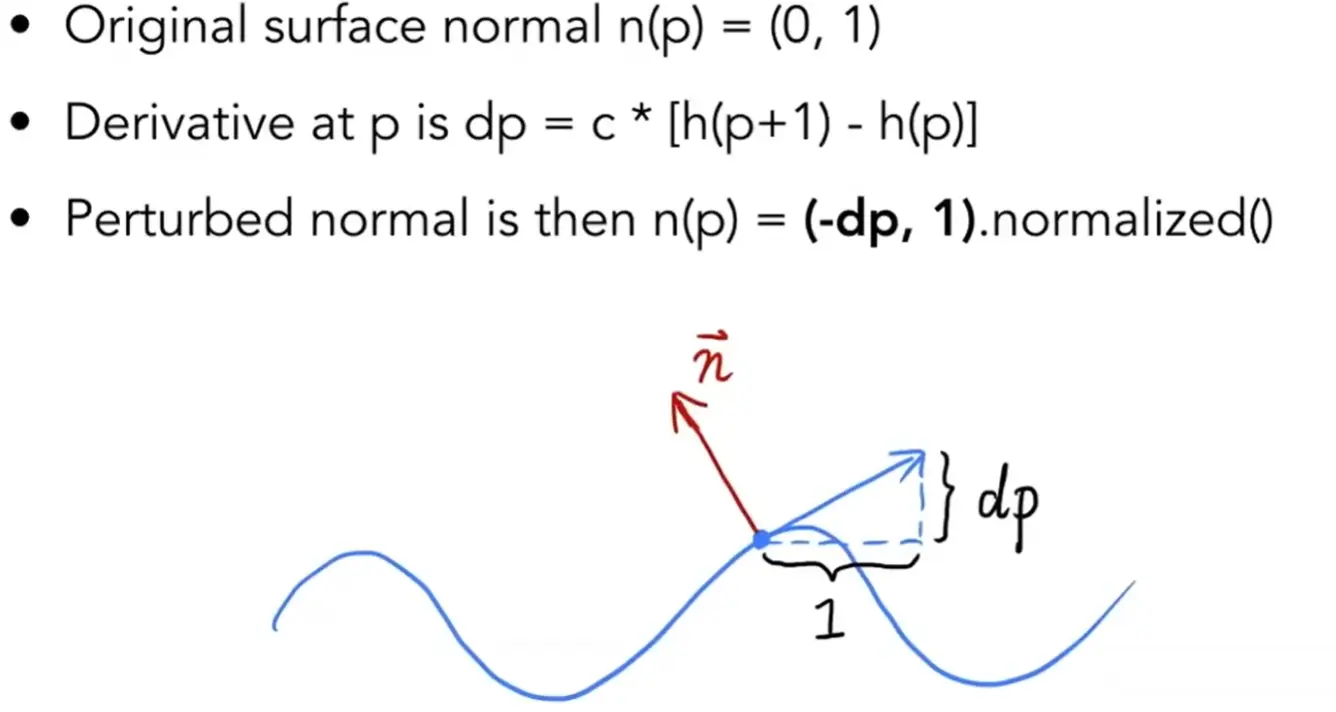
Displacement mapping

Bump mapping limitations

• 边缘看不到起伏
• 凹凸部分无法在物体本身上投下阴影

• 需要模型的三角形要足够细，采样率高于贴图
• direct x: 先有基本的模型，按照需要增加三角形个数

3D Procedural Noise + Solid Modeling

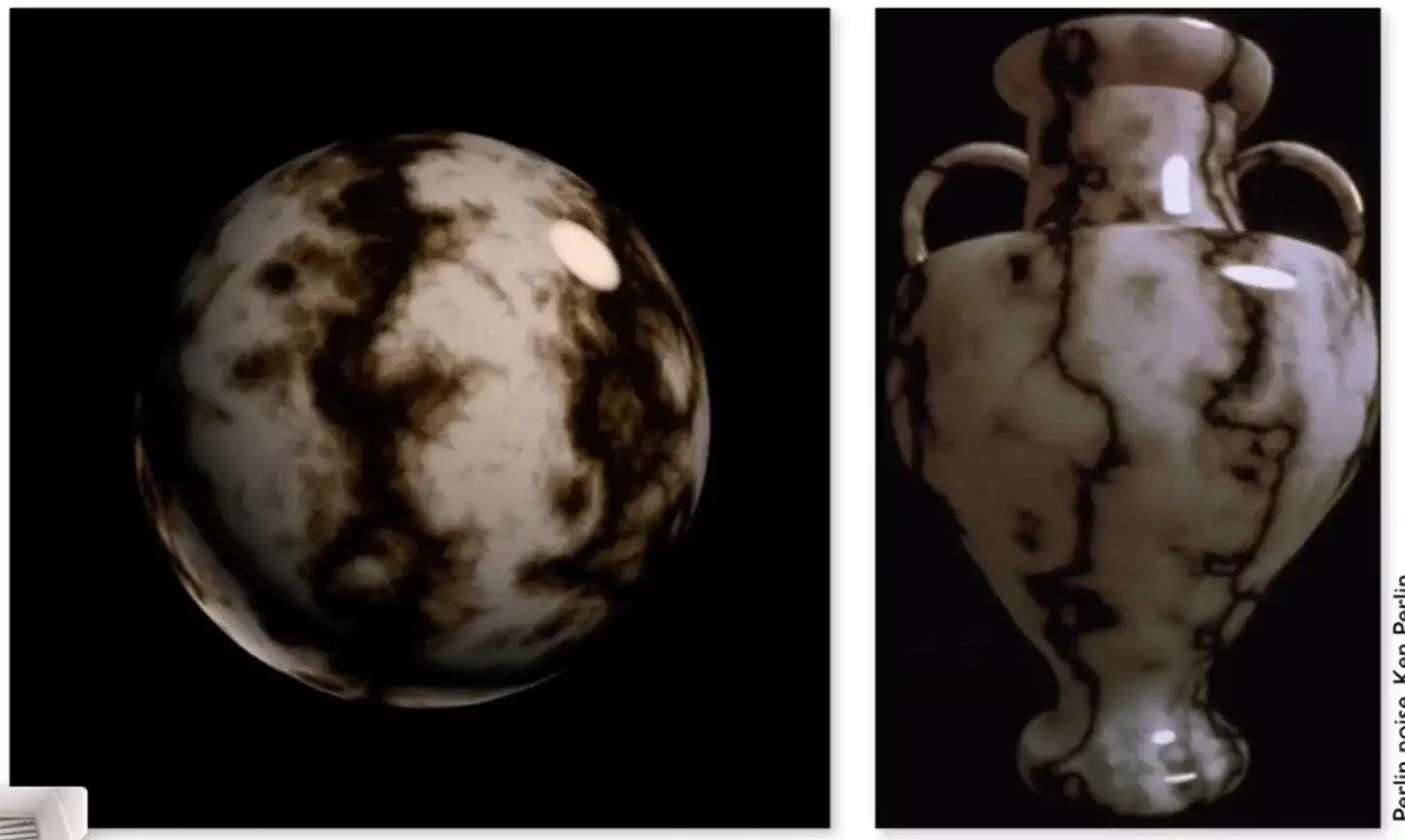
• 柏林噪声

Precomputed shading

3D Textures

Interpolation Across Triangles: Barycentric Coordinates 重心坐标

Barycentric Coordinates

\[\begin{cases} (x,y)&=\alpha A+\beta B+\gamma C \\ \alpha+\beta+\gamma&=1 \end{cases} \implies (\alpha,\beta,\gamma) \]

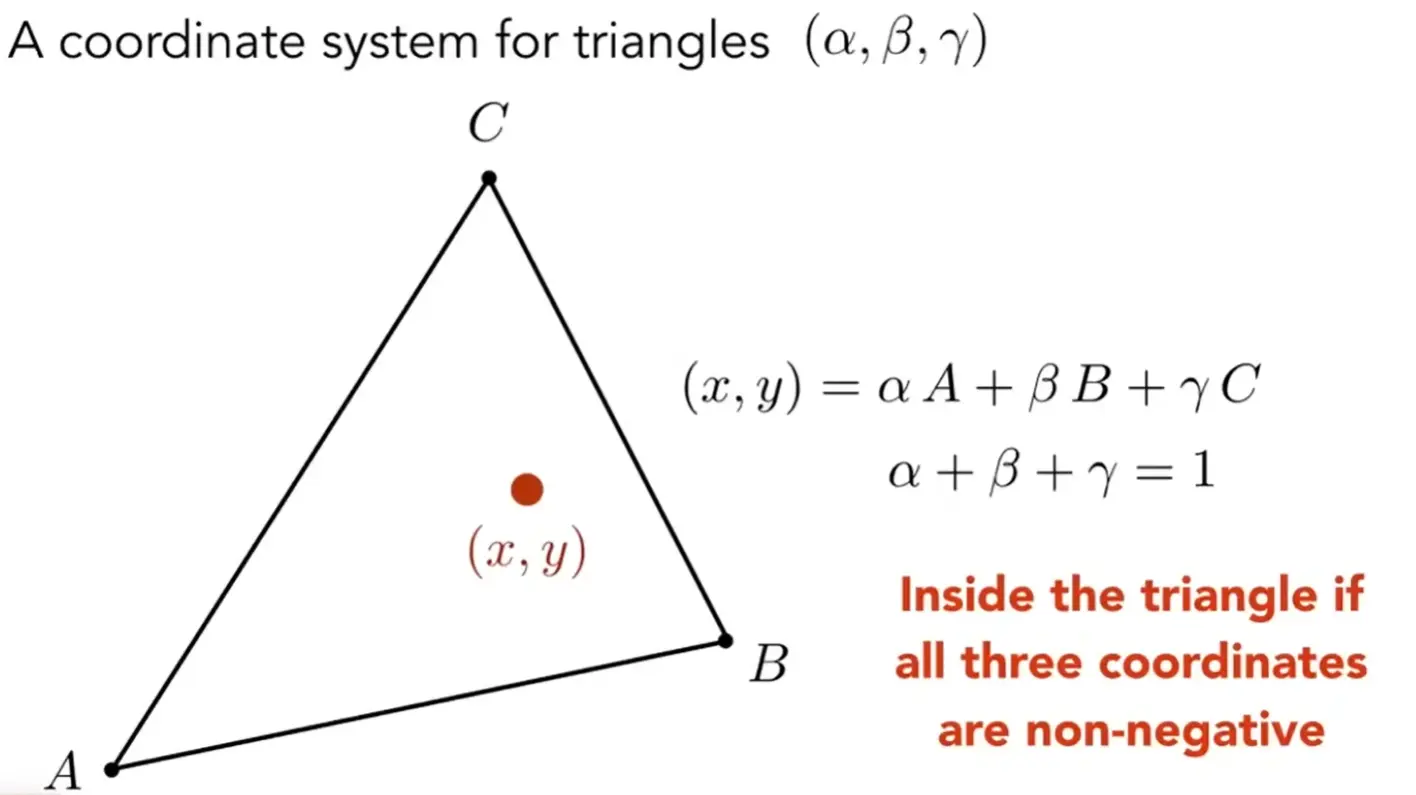
如果 \(\alpha,\beta,\gamma\geq0\)，那么在三角形内。

可以通过面积的比例关系求解重心坐标：

\[\begin{align} \alpha &=\frac{A_A}{A_A+A_B+A_C} \\ \beta &=\frac{A_B}{A_A+A_B+A_C} \\ \gamma &=\frac{A_C}{A_A+A_B+A_C} \end{align}\]

也可以使用公式：

\[\begin{aligned} & \alpha=\frac{-(x-x_B)(y_C-y_B)+(y-y_B)(x_C-x_B)}{-(x_A-x_B)(y_C-y_B)+(y_A-y_B)(x_C-x_B)} \\ & \beta=\frac{-(x-x_C)(y_A-y_C)+(y-y_C)(x_A-x_C)}{-(x_B-x_C)(y_A-y_C)+(y_B-y_C)(x_A-x_C)} \\ & \gamma=1-\alpha-\beta \end{aligned}\]

Using Barycentric Coordinates

\[V=\alpha V_A+\beta V_B+\gamma V_C\]

Warning

空间三角形经过投影之后，重心坐标并不是不变的，所以要先在三维空间中完成插值

Comments