Skip to content

08 Materials and Appearances

Intro#

./__assets/GAMES101 08 Materials and Appearances/IMG-GAMES101 08 Materials and Appearances-20250209231019039.webp

  • 不同的材质与光线的作用不同
  • 画面应该能够体现材质的不同
\[\text{Material}=\text{BRDF}\]

Diffuse / Lambertian Material#

./__assets/GAMES101 08 Materials and Appearances/IMG-GAMES101 08 Materials and Appearances-20250209231358638.webp

在所有方向上积分得到的出射光：

\[\begin{aligned} L_o(\omega_o) & =\int_{H^2}f_rL_i(\omega_i)\cos\theta_i\mathrm{d}\omega_i \\ & =f_rL_i\int_{H^2}(\omega_i)\cos\theta_i\mathrm{d}\omega_i \\ & =\pi f_rL_i \end{aligned}\]

由于假设 \(L_{i}=L_{o}\)，得到 \(f_{r}=\frac{1}{\pi}\)，就是不吸收情况下的均匀漫反射，可以考虑吸收：

\[f_{r}=\frac{\rho}{\pi}\quad\rho\text{ is albedo(color) 基础反射率}\]

Glossy Material#

400

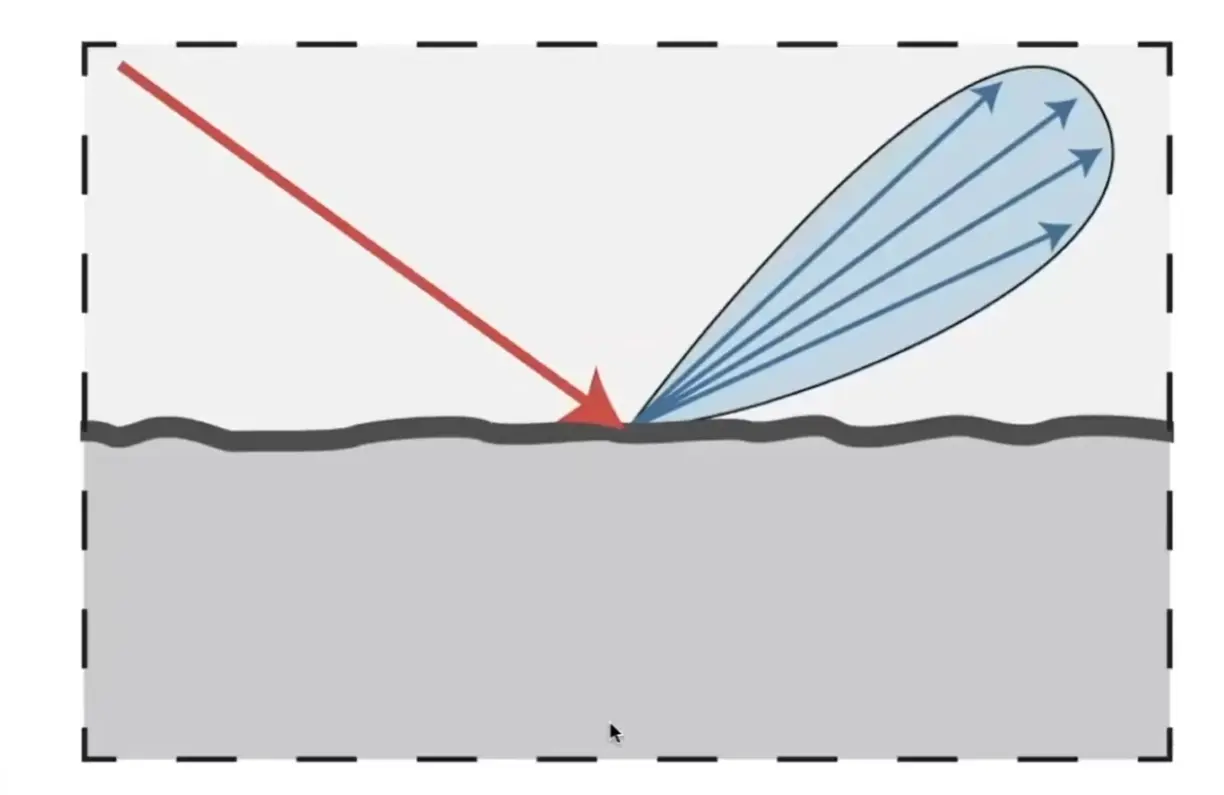
Ideal Reflective / Refractive Material (BSDF)#

S 表示散射，包括反射和折射

400

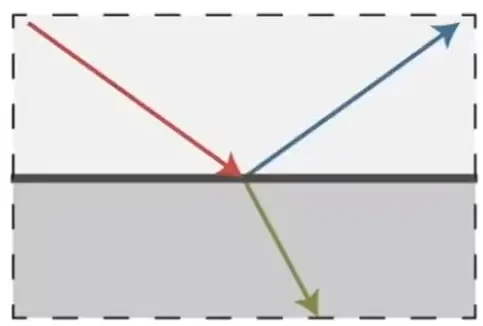
Perfect Specular Reflection#

400

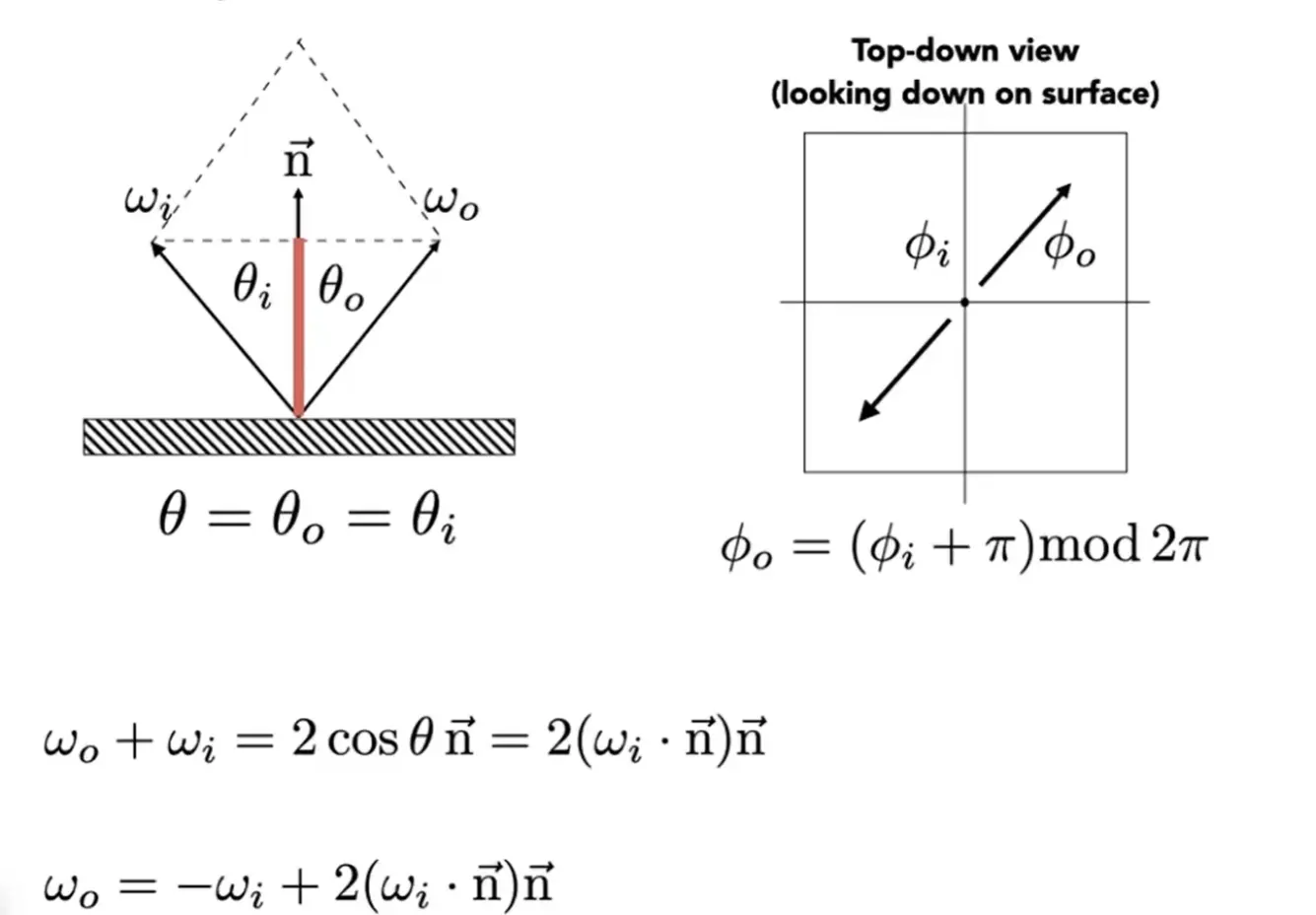
Specular Refraction#

400

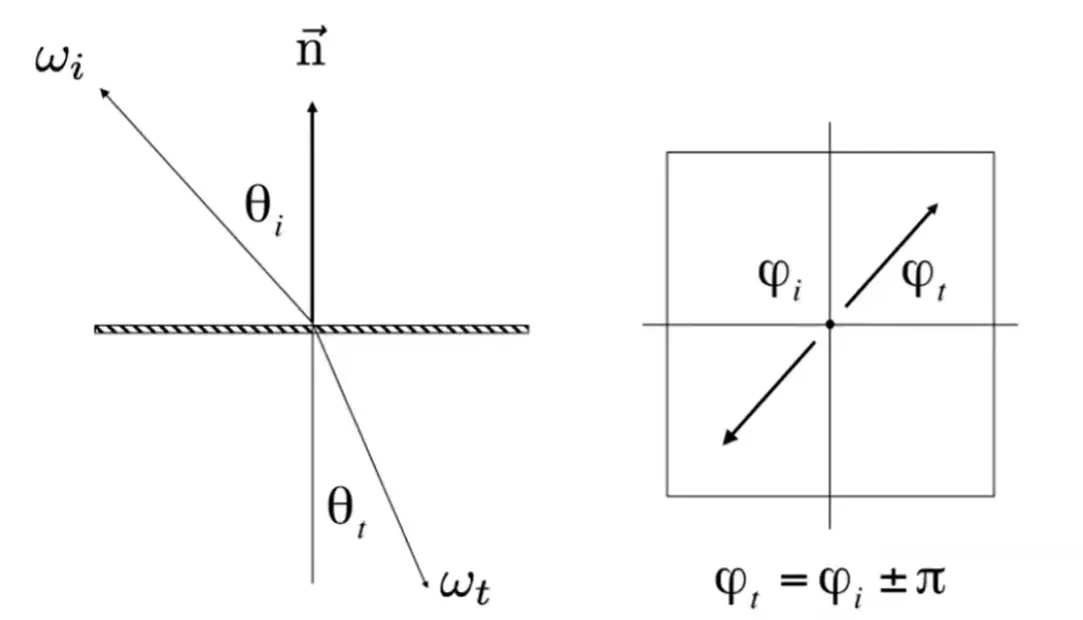
\[\eta_{i}\sin \theta_{i}=\eta_{t}\sin \theta_{t}\]

全反射，光密介质到光疏介质，折射角为 90°

Fresnel Term#

500

不同角度的反射率不同

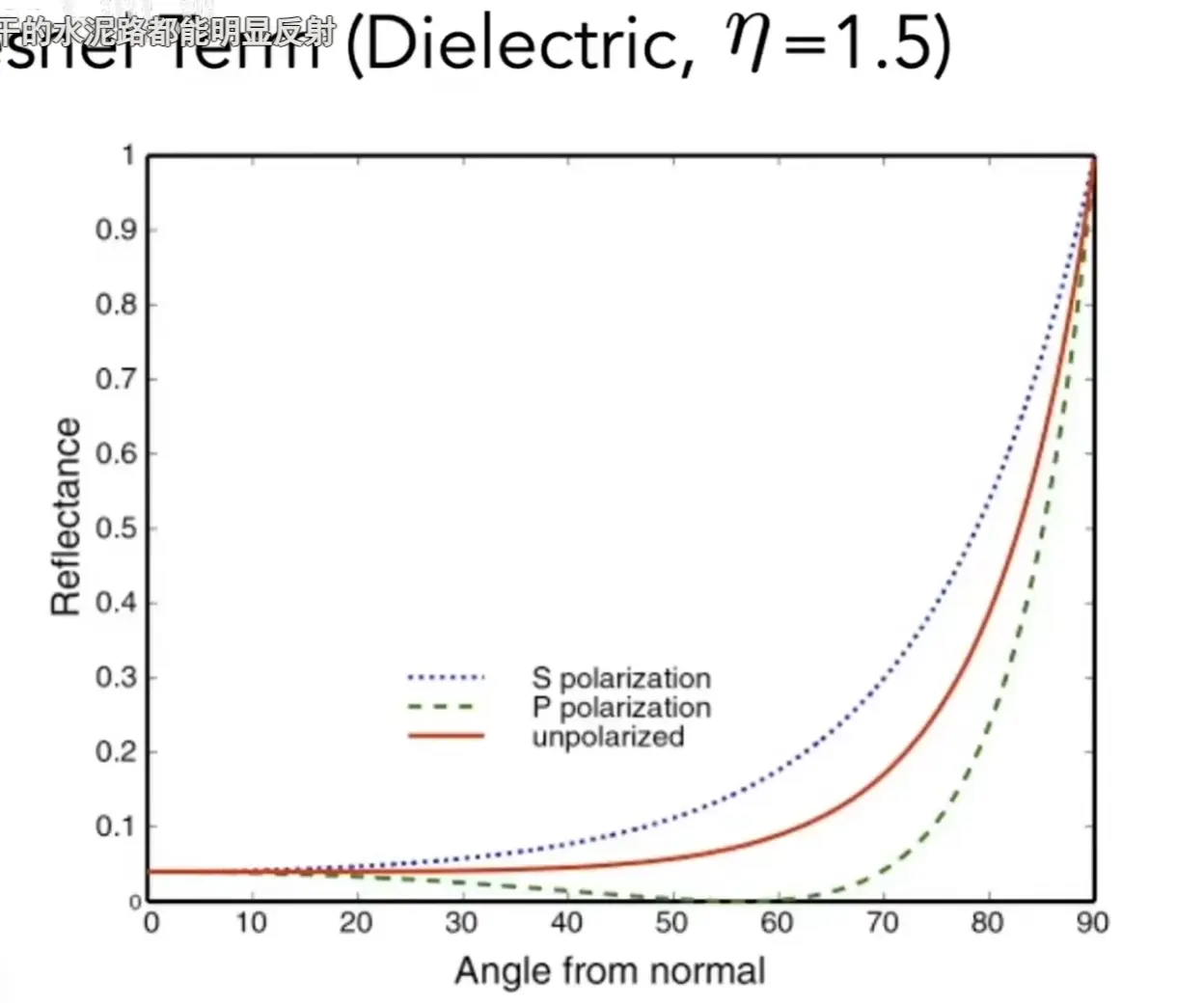
500x417

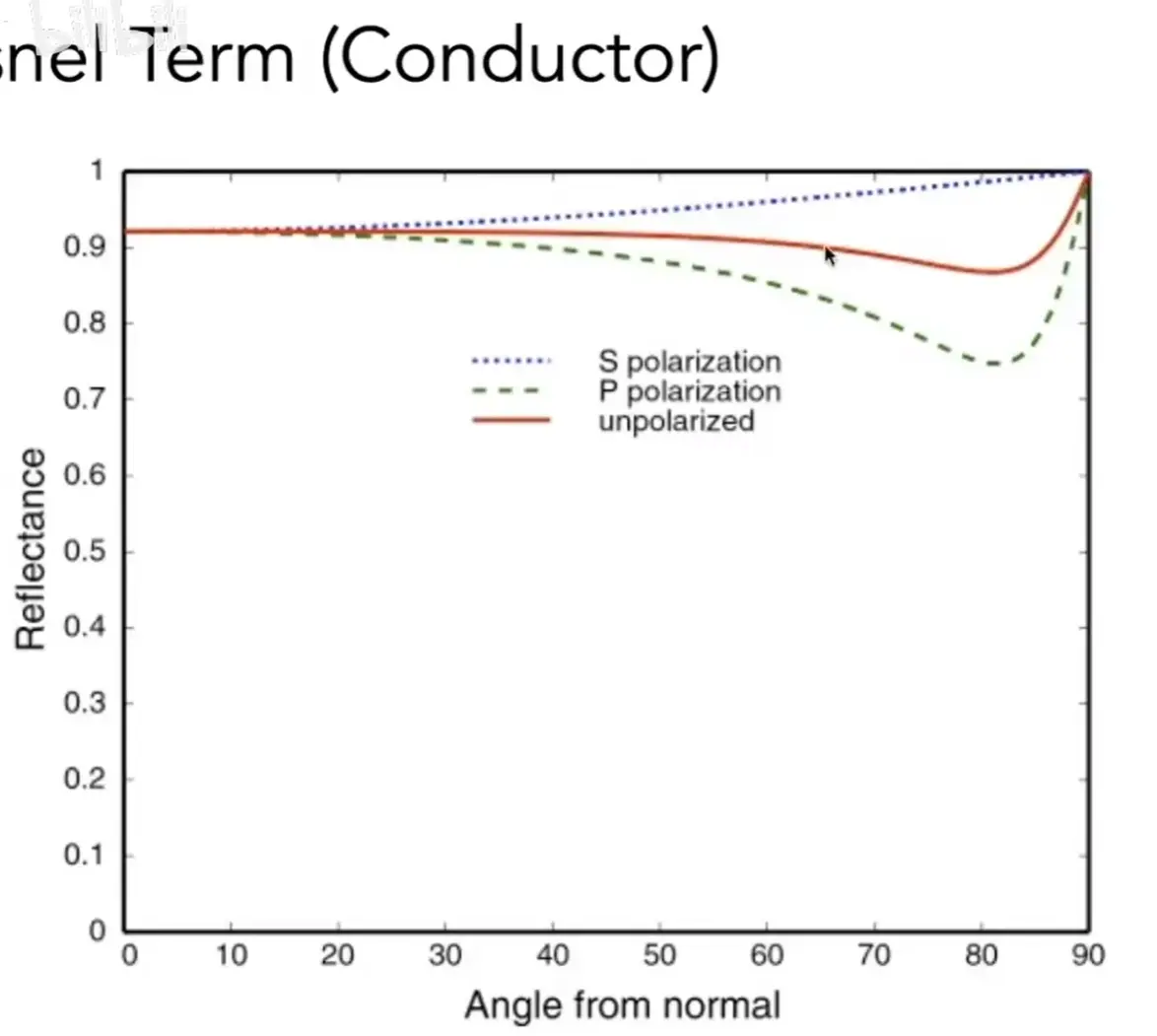
500x448

Note

导体和绝缘体的变化趋势不同

\[\begin{align} R_s&=\left|\frac{n_1\cos\theta_i-n_2\cos\theta_i}{n_1\cos\theta_i+n_2\cos\theta_i}\right|^2=\left|\frac{n_1\cos\theta_i-n_2\sqrt{1-\left(\frac{n_1}{n_2}\sin\theta_i\right)^2}}{n_1\cos\theta_i+n_2\sqrt{1-\left(\frac{n_1}{n_2}\sin\theta_i\right)^2}}\right|^2 \\ R_p&=\left|\frac{n_1\cos\theta_i-n_2\cos\theta_i}{n_1\cos\theta_i+n_2\cos\theta_i}\right|^2=\left|\frac{n_1\sqrt{1-\left(\frac{n_1}{n_2}\sin\theta_i\right)^2}-n_2\cos\theta_i}{n_1\sqrt{1-\left(\frac{n_1}{n_2}\sin\theta_i\right)^2}+n_2\cos\theta_i}\right|^2\\ R_{\mathrm{eff}}&=\frac{1}{2}\left(R_{\mathrm{s}}+R_{\mathrm{p}}\right) \end{align}\]

Approximate: Schlick's approximation#

\[\begin{aligned} R(\theta) & =R_0+(1-R_0)(1-\cos\theta)^5 \\ R_{0} & =\left(\frac{n_1-n_2}{n_1+n_2}\right)^2 \end{aligned}\]

Microfacet Material#

Note

从远处看，表面上微小的粗糙部分几乎没有影响，看到的就是光滑的表面

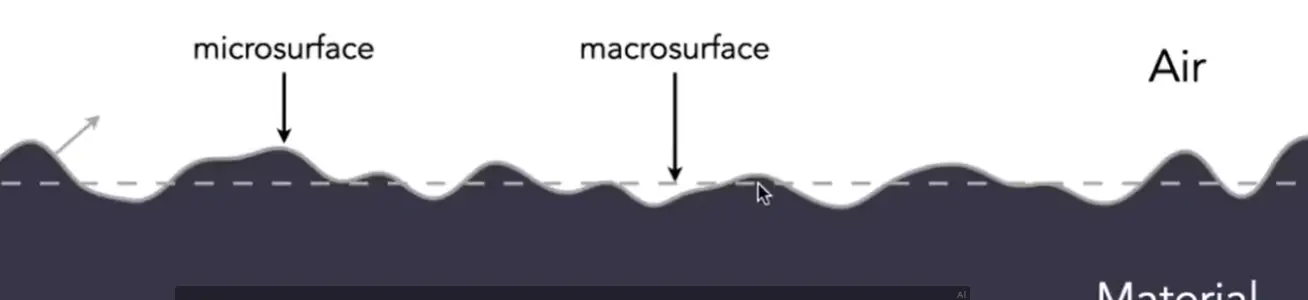
500x115

  • 从远处看，当作平面+纹理
  • 从近处看，当作几何模型

Microfacet BRDF#

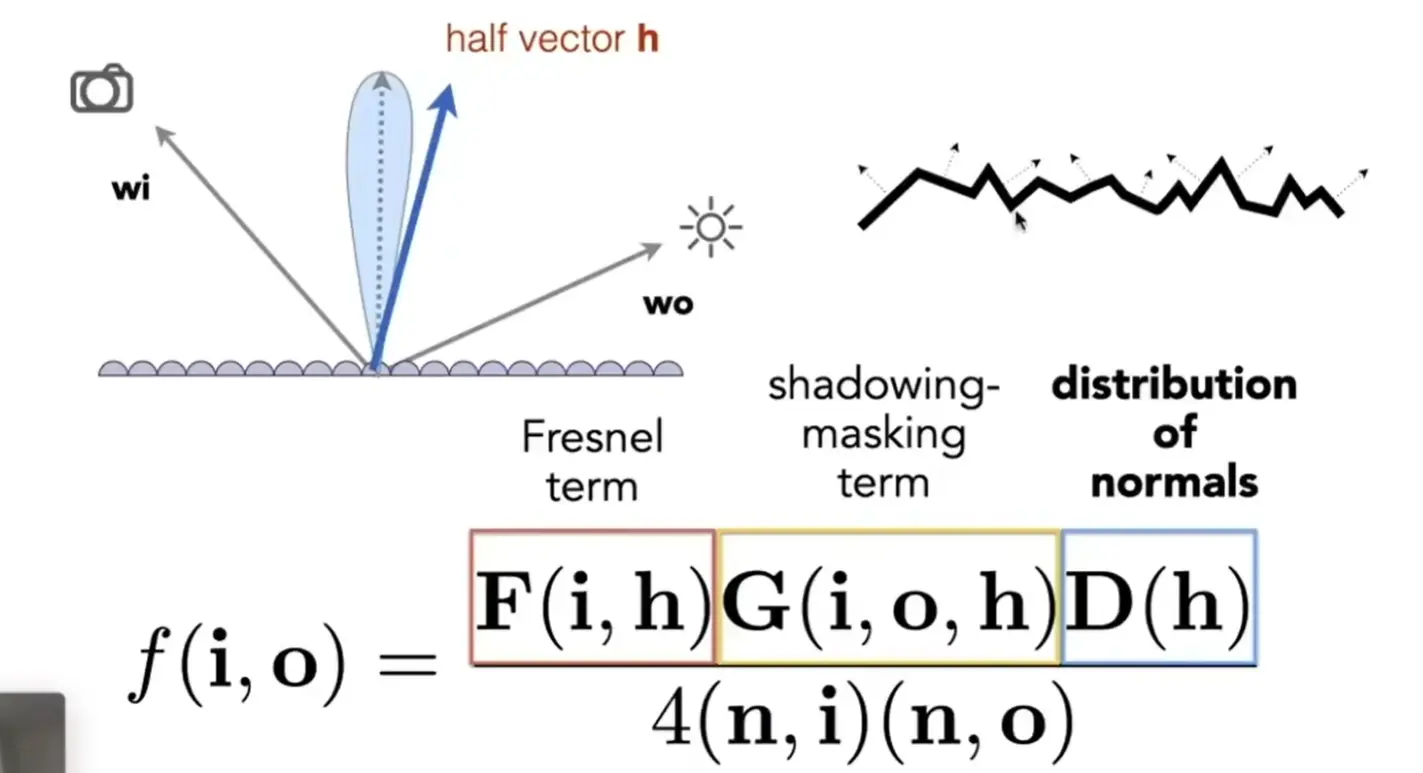
500x272

  • F 菲涅尔项，角度影响反射率
  • G shadowing-masking term 微表面可能相互遮挡，导致亮度下降
  • D 法向量分布，就是求出有多少法向量沿着半程向量方向，这样的向量才能正确将光反射到视野中

Isotropic / Anisotropic Materials#

各向同性/各向异性材质

500x260

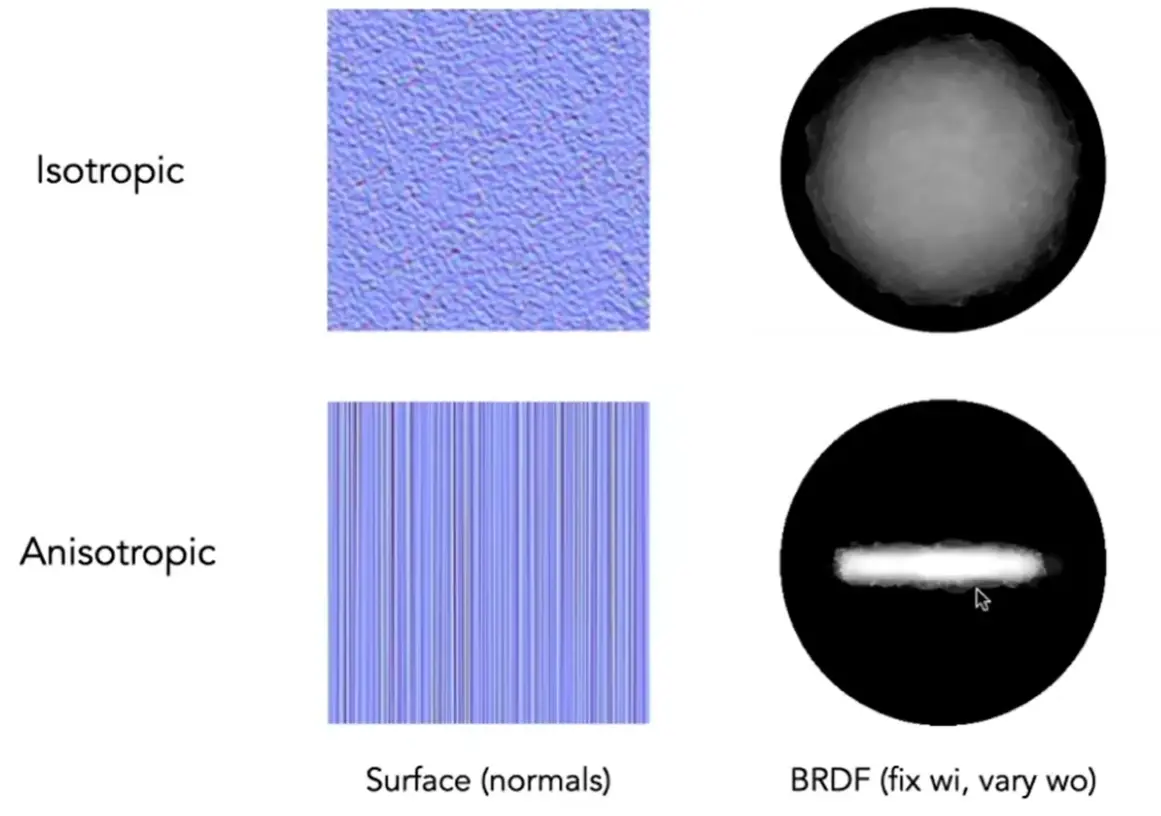
500x351

Note

  • 例如磨过的金属是各向异性微表面
  • 各向异性 BRDF 与方位角 \(\phi\) 有关

Properties of BRDFs#

  • 非负性
  • 线性性，可以将 BRDF 拆成很多种，分别计算然后相加
  • 可逆性(reciprocity)，沿着逆向光路的 BRDF 值完全一样
  • 能量守恒，出射能量之和不会超过入射能量之和
  • isotropic vs. anisotropic
    • isotropic: \(f_r(\theta_i,\phi_i;\theta_r,\phi_r)=f_r(\theta_i,\theta_r,\phi_r-\phi_i)\)
    • 根据 reciprocity: \(f_r(\theta_i,\theta_r,\phi_r-\phi_i)=f_r(\theta_r,\theta_i,\phi_i-\phi_r)=f_r(\theta_i,\theta_r,|\phi_r-\phi_i|)\) 只用考虑方位角的差

Measuring BRDFs#

500x242

Comments