07 Ray Tracing

Intro

why ray tracing? rasterization couldn't handle global effects well

• soft shadow
• glossy reflection
• indirect illumination

• Ray tracing s accurate, but very slow
  • rasterization: real-time, ray tracing: offline

Light Rays

1. 沿直线传播
2. 不会相互碰撞
3. 从光源到相机，可逆性 (reciprocity)

Ray Casting

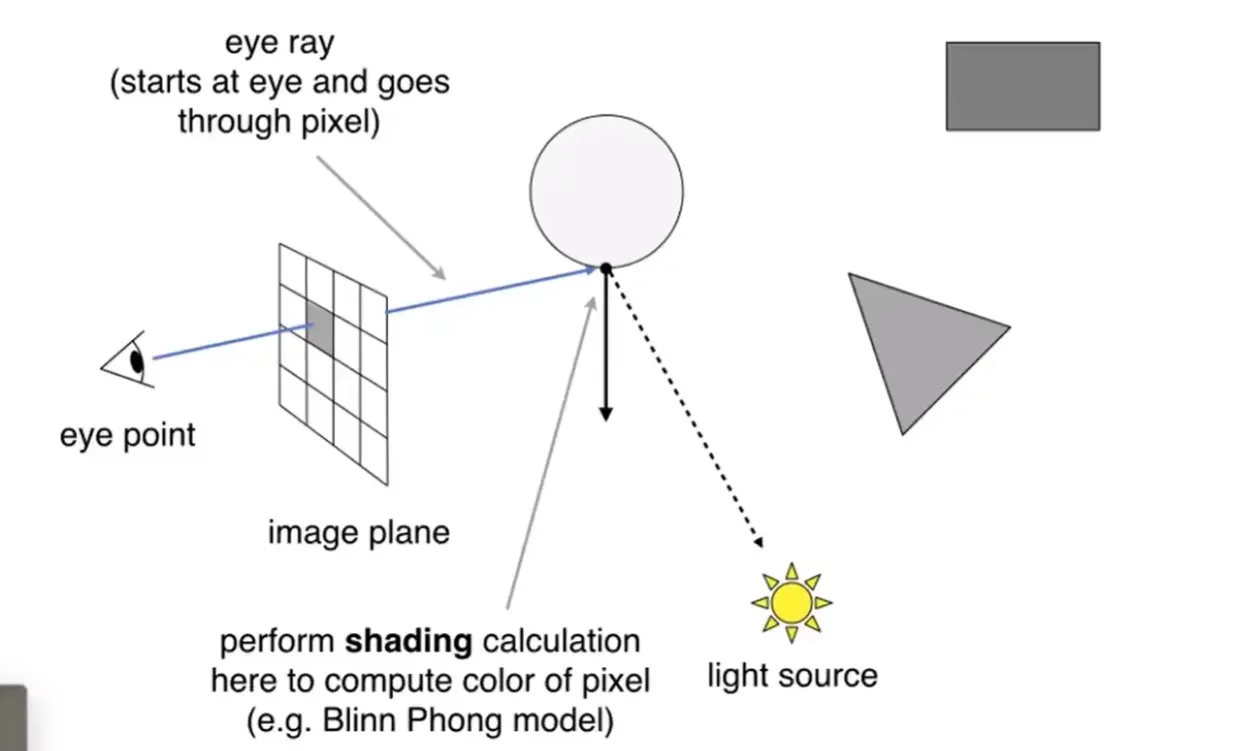
1. 对每个像素投射一束光线
2. 光线遇到场景中的一个点，判断这个点是否对光源可见
3. 依据光照情况，渲染像素颜色

problem

仍然忽略了折射

Recursive (Whitted-Style) Ray Tracing

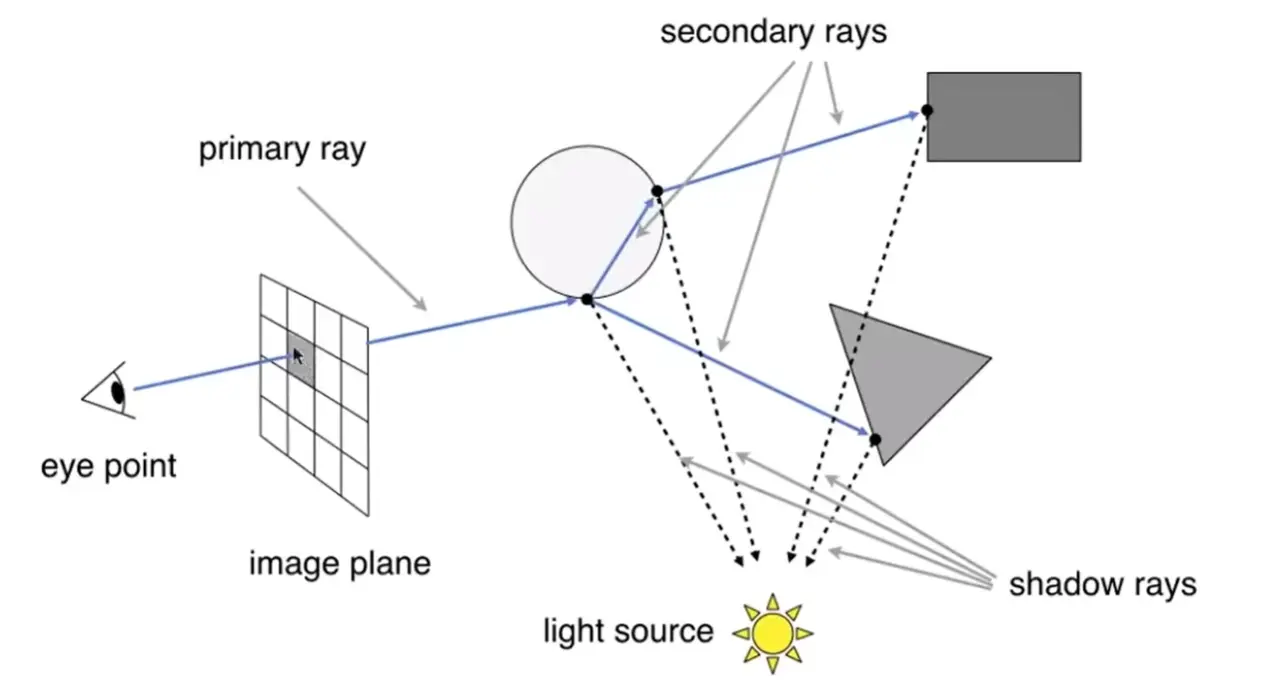
Ray Equation

\[\begin{aligned} \mathbf{r}(t)=\mathbf{o}+t\mathbf{d}\quad0\leq t<\infty \end{aligned}\]

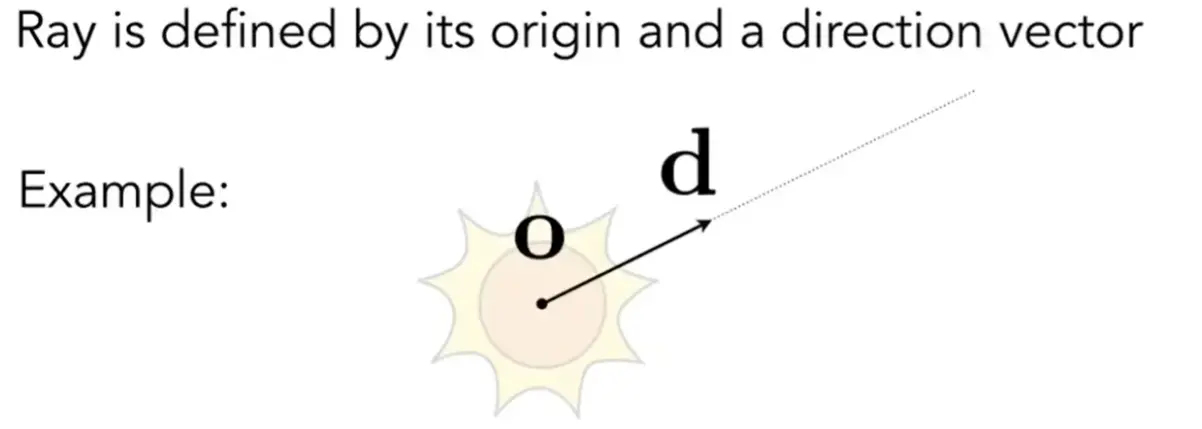
Ray Intersection

with sphere

\[ \begin{cases} \mathbf{r}(t)=\mathbf{o}+t\mathbf{d}\quad0\leq t<\infty \\ (\mathbf{p}-\mathbf{c})^2-R^2=0 \end{cases}\implies (\mathbf{o}+t\mathbf{d}-\mathbf{c})^2-R^2=0 \]

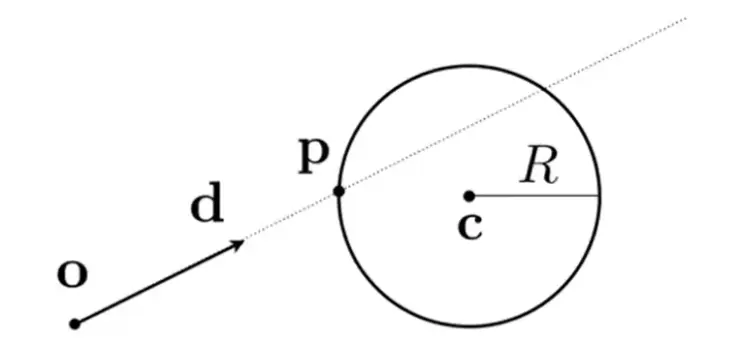
然后计算二次方程：

\[\begin{aligned} & at^{2}+bt+c=0,\mathrm{where} \\ & a=\mathbf{d}\cdot\mathbf{d} \\ & b=2(\mathbf{o-c})\cdot\mathbf{d} \\ & c=(\mathbf{o}-\mathbf{c})\cdot(\mathbf{o}-\mathbf{c})-R^2 \\ & t=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a} \end{aligned}\]

with implicit surface

\[ \begin{cases} \mathbf{r}(t)=\mathbf{o}+t\mathbf{d}\quad0\leq t<\infty \\ f(\mathbf{p})=0 \end{cases}\implies f(\mathbf{o}+t\mathbf{d})=0 \]

with single triangle

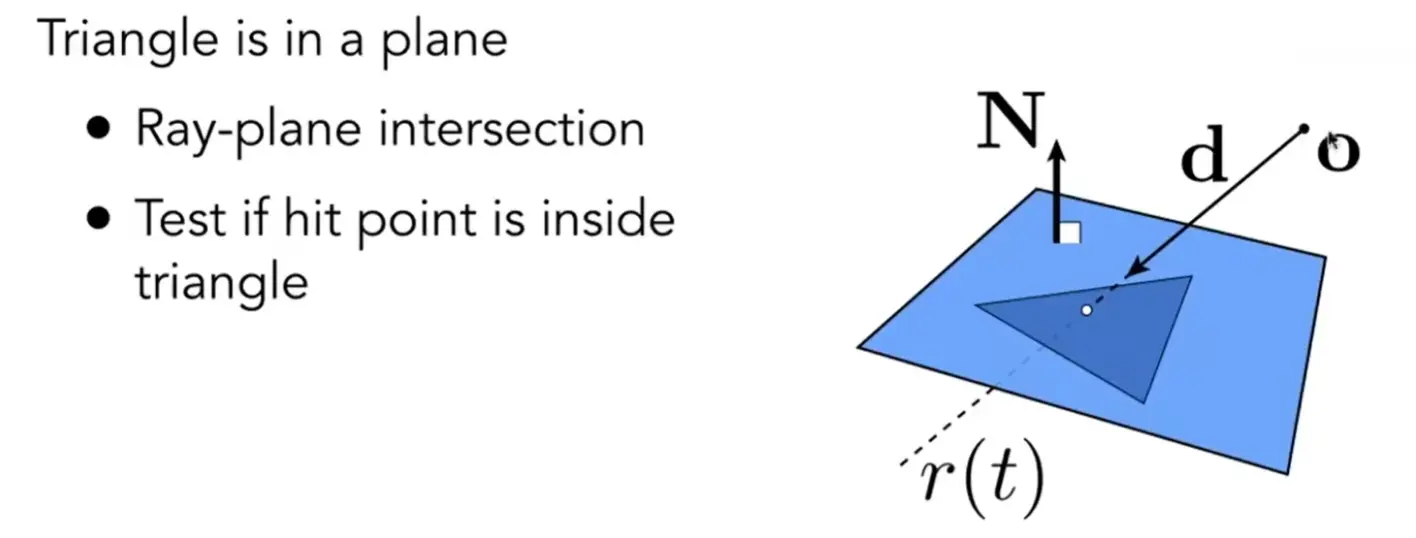
Note

1. 与三角形所在平面相交
2. 判断交点是否在三角形内

Plane Equation

plane equation

\(\mathbf{p}:(\mathbf{p}-\mathbf{p}^{\prime})\cdot\mathbf{N}=0 \implies ax+by+cz+d=0\)

\[\begin{aligned} & \mathrm{Set~}\mathbf{p}=\mathbf{r}(t)\text{ and solve for }t \\ & (\mathbf{p}-\mathbf{p}^{\prime})\cdot\mathbf{N}=(\mathbf{o}+t\mathbf{d}-\mathbf{p}^{\prime})\cdot\mathbf{N}=0 \\ & t=\frac{(\mathbf{p}^{\prime}-\mathbf{o})\cdot\mathbf{N}}{\mathbf{d}\cdot\mathbf{N}} & \mathrm{Check:~}0\leq t<\infty \end{aligned}\]

Moller Trumbore Algorithm

直接求解重心坐标，判断是否有 \(1-b_{1}-b_{2},b_{1},b_{2}\geq0\)

\[\begin{align} \vec{\mathbf{O}}+t\vec{\mathbf{D}}&=(1-b_{1}-b_{2})\vec{\mathbf{P}}_{0}+b_{1}\vec{\mathbf{P}}_{1}+b_{2}\vec{\mathbf{P}}_{2} \\ \implies \begin{bmatrix} t \\ b_1 \\ b_2 \end{bmatrix}&=\frac{1}{\vec{\mathbf{S}}_1\bullet\vec{\mathbf{E}}_1} \begin{bmatrix} \vec{\mathbf{S}}_2\bullet\vec{\mathbf{E}}_2 \\ \vec{\mathbf{S}}_1\bullet\vec{\mathbf{S}} \\ \vec{\mathbf{S}}_2\bullet\vec{\mathbf{D}} \end{bmatrix} \\ \text{where }& \begin{cases} & \mathbf{\vec{E}}_{1}=\mathbf{\vec{P}}_{1}-\mathbf{\vec{P}}_{0} \\ & \mathbf{\vec{E}}_{2}=\mathbf{\vec{P}}_{2}-\mathbf{\vec{P}}_{0} \\ & \mathbf{\vec{S}}=\mathbf{\vec{O}}-\mathbf{\vec{P}}_{0} \\ & \mathbf{\vec{S}}_{1}=\mathbf{\vec{D}}\times\mathbf{\vec{E}}_{2} \\ & \mathbf{\vec{S}}_{2}=\mathbf{\vec{S}}\times\mathbf{\vec{E}}_{1} \end{cases} \end{align}\]

with triangle mesh

naive solution

每个三角形面都判断光线是否过三角形

Bounding Volumes

如果光线和包围盒不相交，一定不会与盒中的物体相交

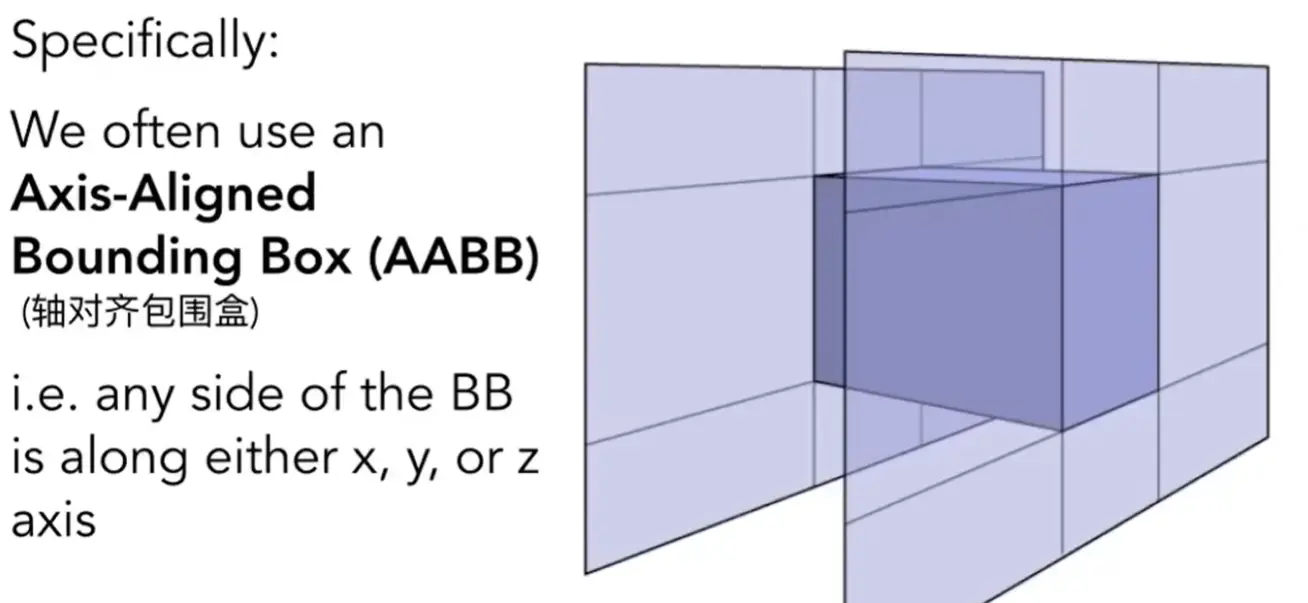
Axis-Aligned Bounding Box (AABB)

• 任何一个面都是与坐标轴面平行的
• 横平竖直的平面求解交点更加方便

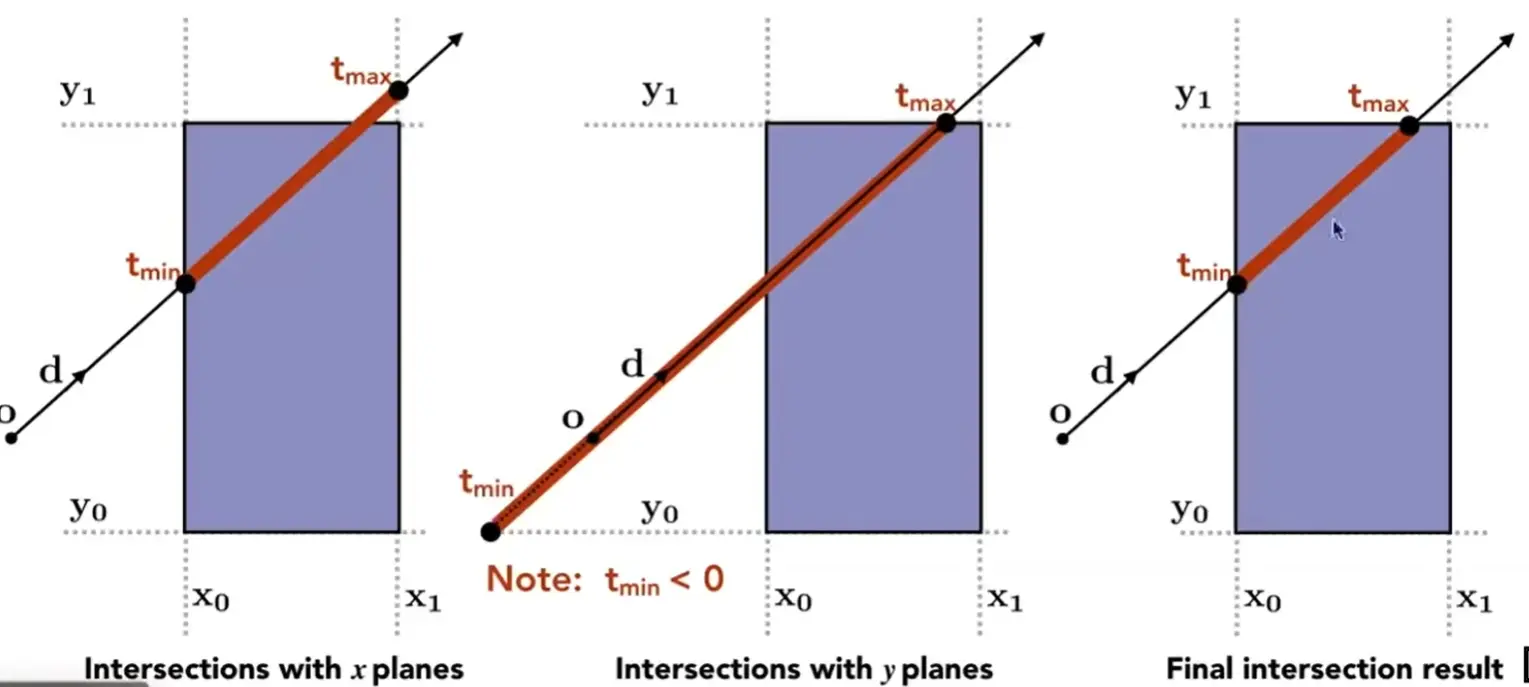
Note

• 分别求出穿过三组对面的 \(t_{\text{min}},t_{\text{max}}\)
• 求交集 \(t_{\text{enter}}=\max\{t_{\text{min}}\}, t_{{\text{exit}}}=\min\{t_{\text{max}}\}\)
  • 最晚进入一个对面的时间是进入盒子时间
  • 最早离开一个对面的时间是离开盒子时间
• 如果 \(t_{\text{enter}}<t_{\text{exit}}\)，那么相交

ray is not a line

• \(t_{\text{exit}}<0\)，盒子在光线后面，不会相交
• \(t_{\text{exit}}\geq 0, t_{\text{enter}}<0\)，光源在盒子里面
• \(t_{\text{exit}}\geq 0,t_{\text{enter}}<t_{\text{exit}}\)，那么相交

Uniform Spatial Partitions (Grids)

假设

• 与 AABB 的求交非常快
• 与物体的求交相对较慢

Preprocess - Build Acceleration Grid

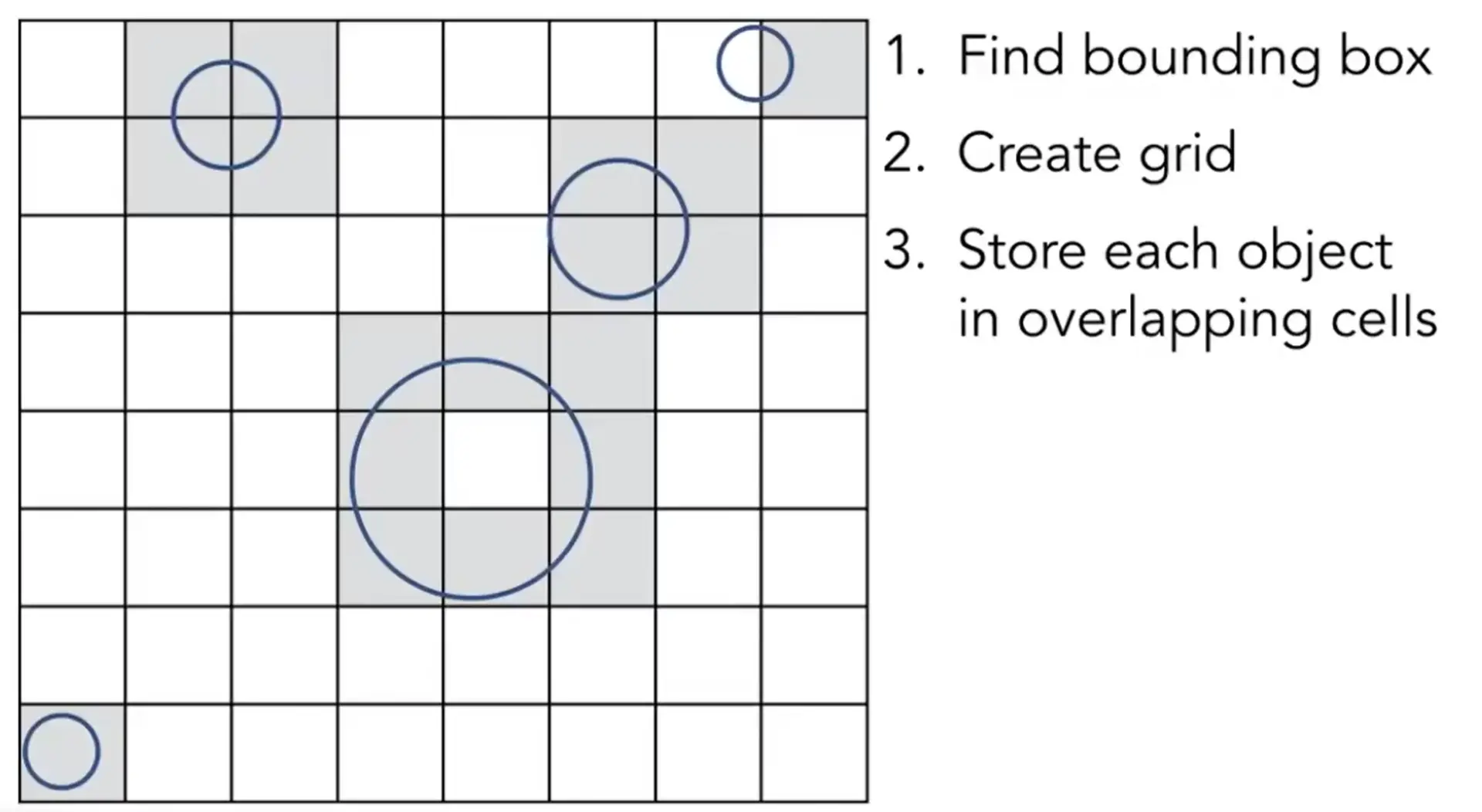
Note

1. 找到一个大的包围盒
2. 内部划分网格
3. 记录有物体的网格

Process

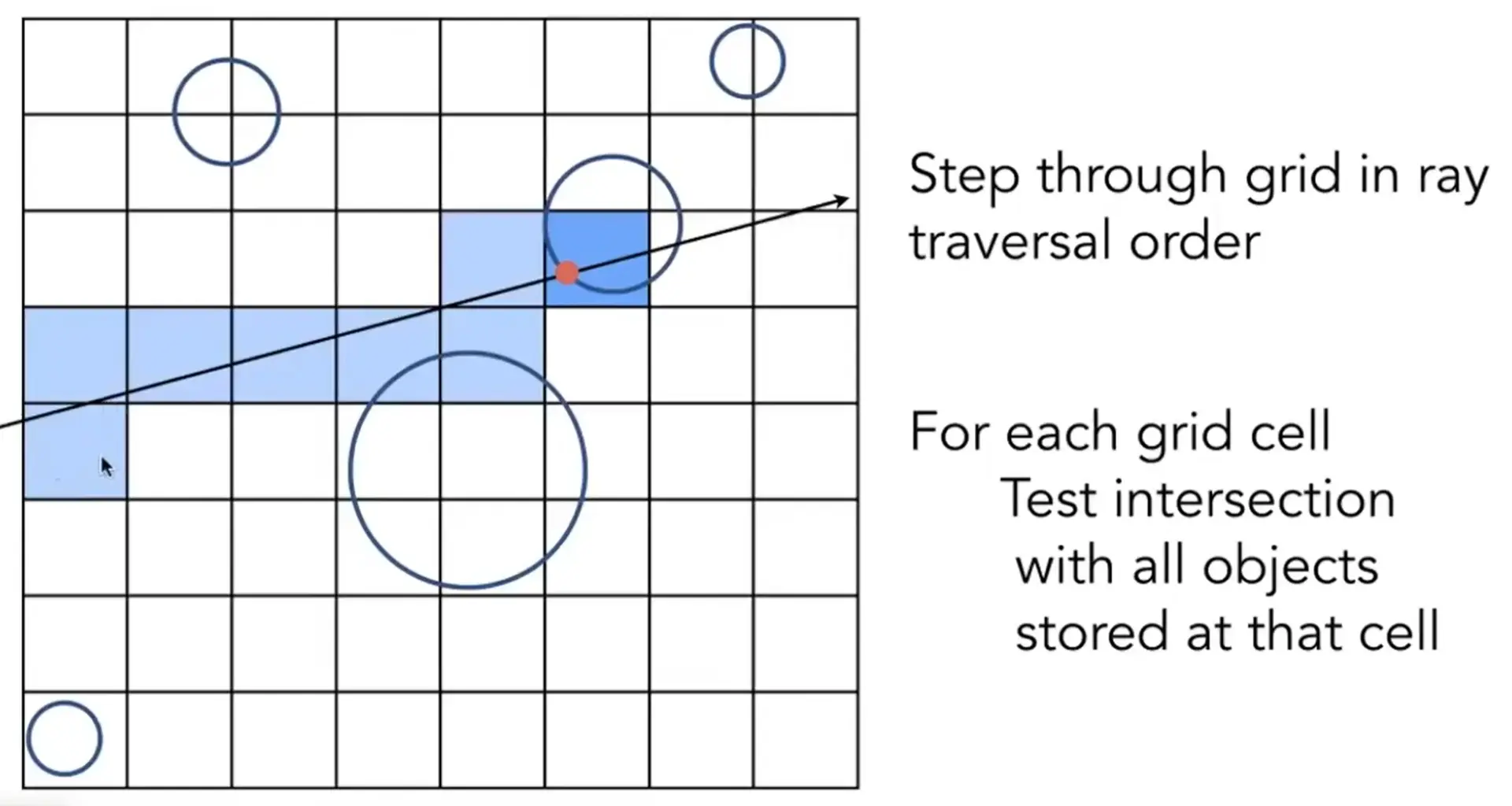
Note

• 光线与一个盒子相交时，下一个相交的盒子只可能是右边或者上面的格子
• 直到与有物体的盒子相交时，进行与物体相交求解

performance

• 格子太稀疏，或者格子太密集，加速效果都不好
• \(\#\text{cells}=C\cdot\#\text{objs}, C\approx 27\text{ in 3D}\)

performance

• 物体分布均匀时，效率高
• 空的部分太多时，效率低

Spatial Partioning

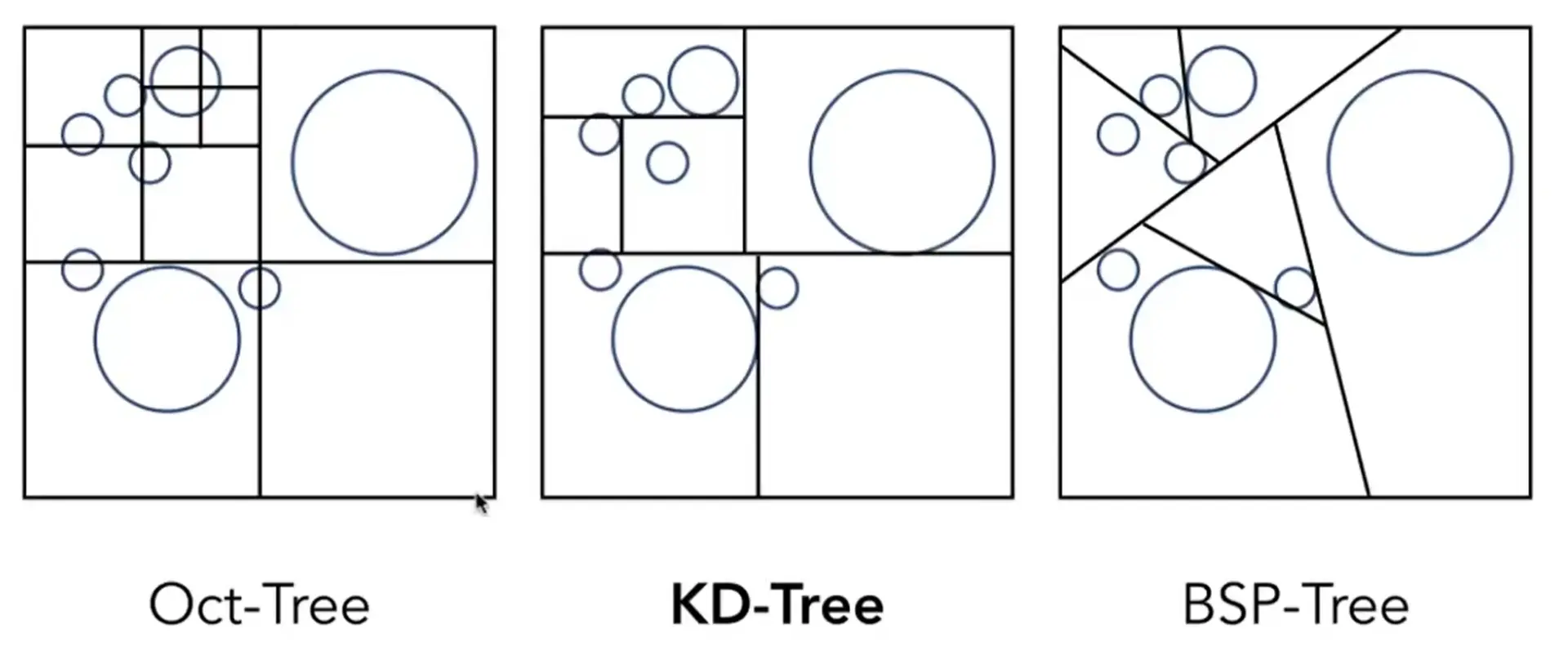
Note

• Oct-Tree: 一直划分，直到格子里的物体数量小于阈值
• KD-Tree: 分别垂直于 x y z 轴进行递归划分
• BSP-Tree: 维度高的时候计算复杂

KD-Tree

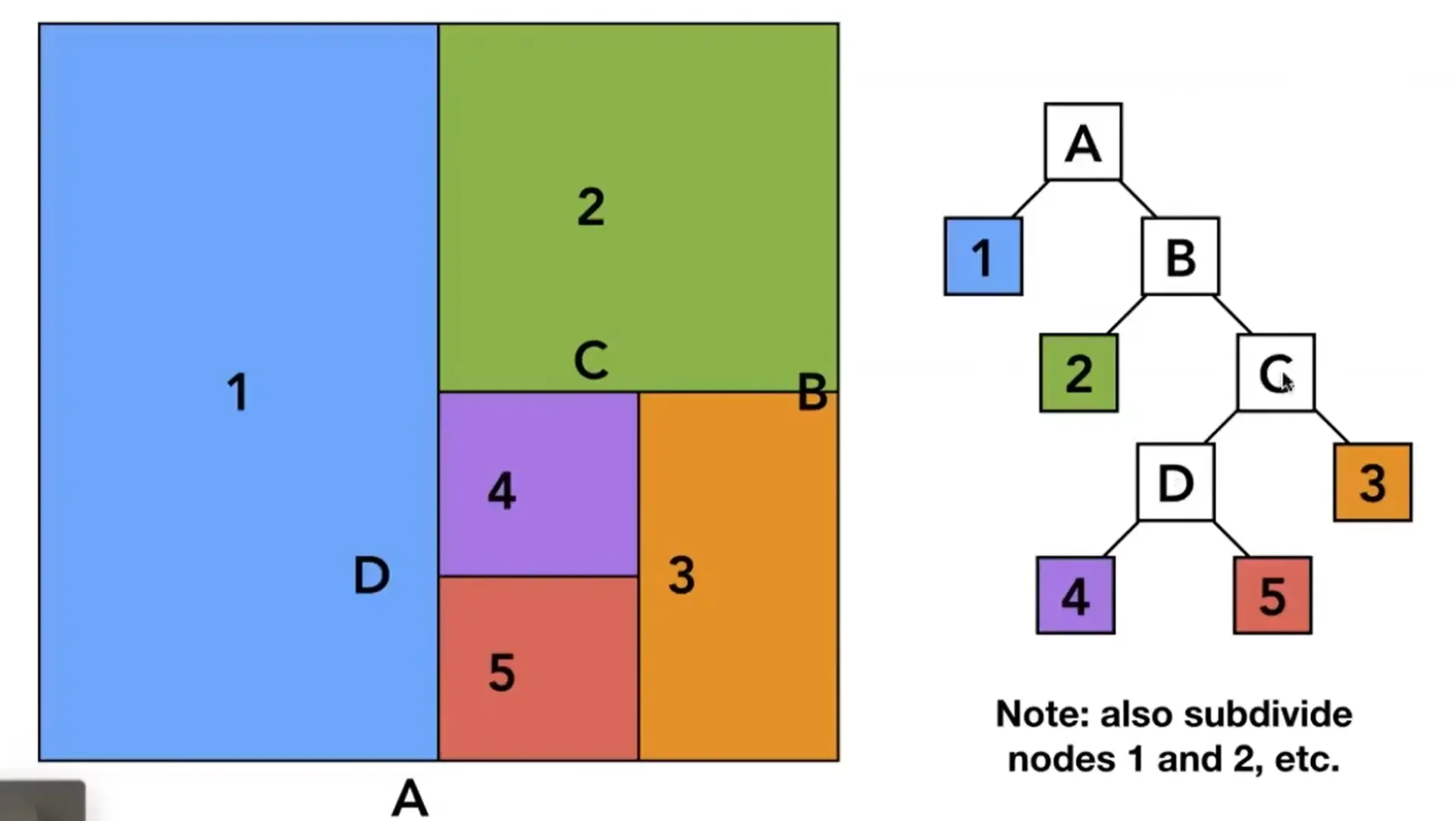
Note

Huffman Tree，在中间节点存储子节点指针

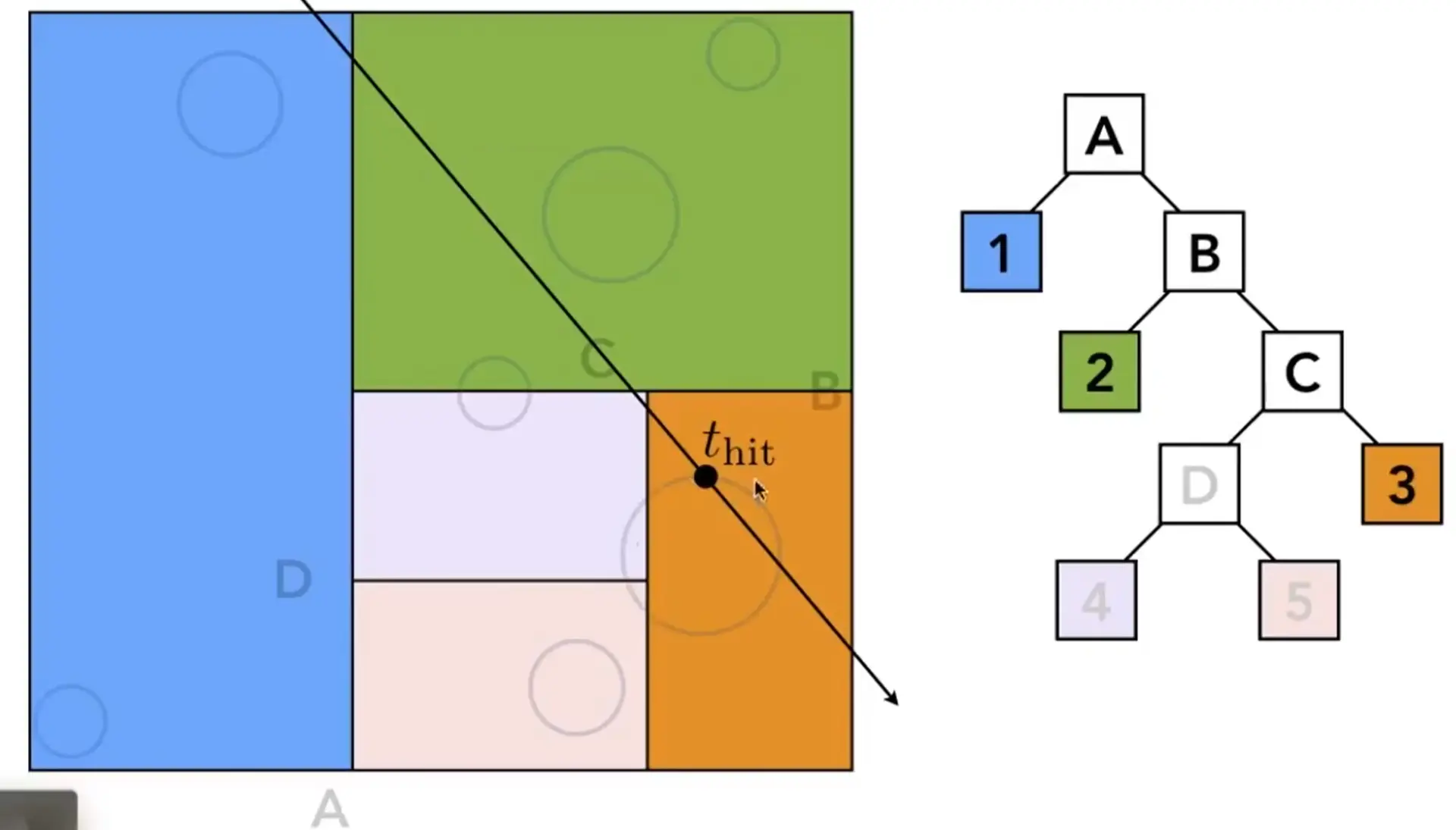
Note

• 与一个节点的 AABB 有交点，则需要判断与其子节点是否有交点，直到叶子节点
• 判断与最小叶子节点内物体是否有交点

Bug

• 判断一个三角形与 AABB 相交比较复杂，即使三个顶点都不在盒子内，也可能相交
• 一个物体可能和不同的盒子都有交集，会出现在多个叶子节点里

Object Partition & Bounding Volume Hierarchy (BVH)

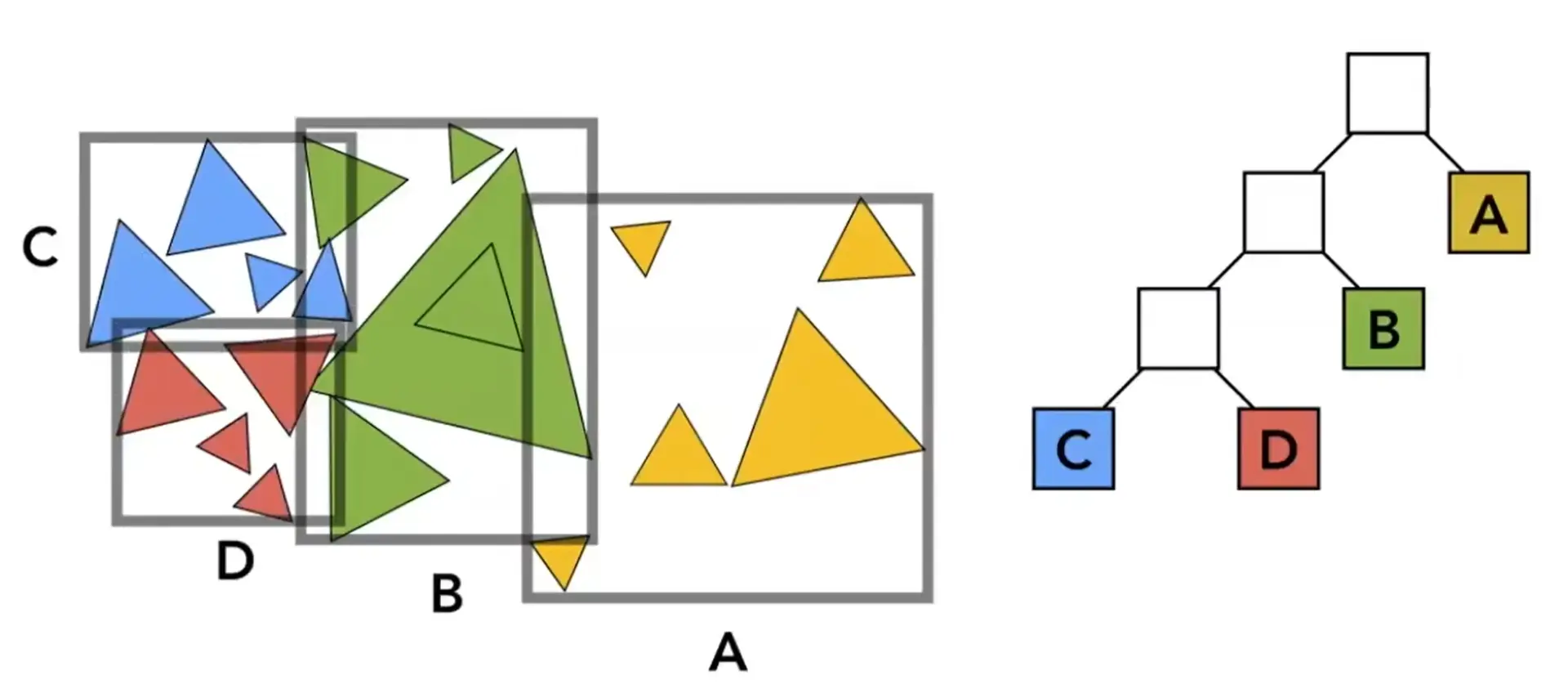
Note

• 将 bounding box 内的物体划分为两个部分，重新计算 bounding box，直到叶子节点有足够少的三角形
• bounding box 可能相交，重叠部分越小越好

how to subdivide?

• choose a dimension to split
• heuristic #1: 总是分割最长的轴
• heuristic #2: split node at location of median object, 让两边的三角形个数相近

Note

场景变化后，要重新计算 BVH

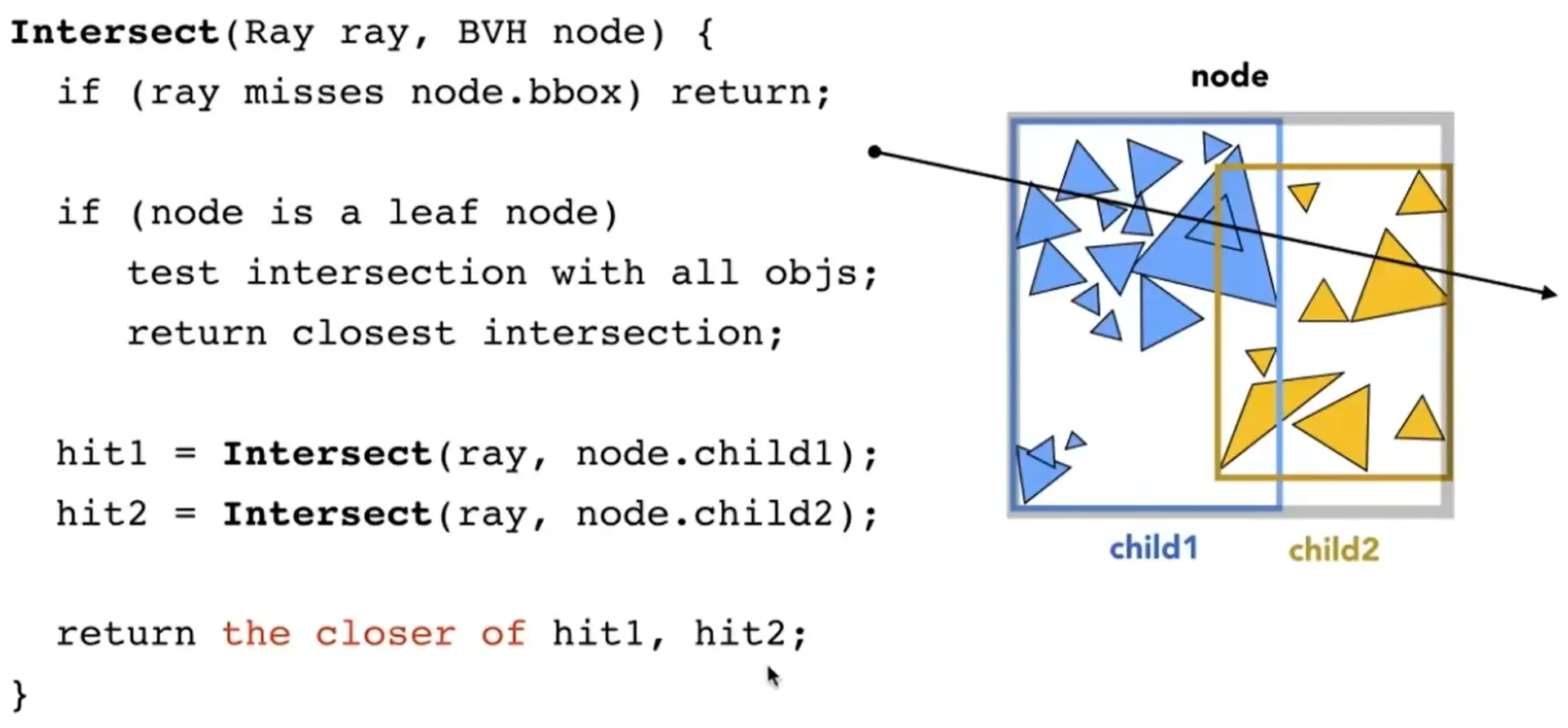
Note

实际应用中 BVH 的应用更加广泛

Basic Radiometry (辐射度量学)

motivation

要让场景更加真实，需要精确地定义光的属性，不能随便定义各种参数

Radiant Energy and Flux (Power)

Basic concepts

Radiant Energy: 电磁辐射的能量

\[Q\text{ [J = Joule]}\]

Radiant Flux (power): 单位时间辐射能量 #photons flowing through a sensor in unit time

\[\Phi\equiv\frac{\mathrm{d}Q}{\mathrm{d}t}\mathrm{[W=Watt]}\mathrm{[lm=lumen]}^{\star}\]

Radiant Intensity: the power per unit solid angle (立体角)

\[\begin{aligned} I(\omega) \equiv\frac{\mathrm{d}\Phi}{\mathrm{d}\omega} \left[\frac{\mathrm{W}}{\mathrm{sr}}\right]\left[\frac{\mathrm{lm}}{\mathrm{sr}} =\mathrm{cd}=\mathrm{candela}\right] \end{aligned}\]

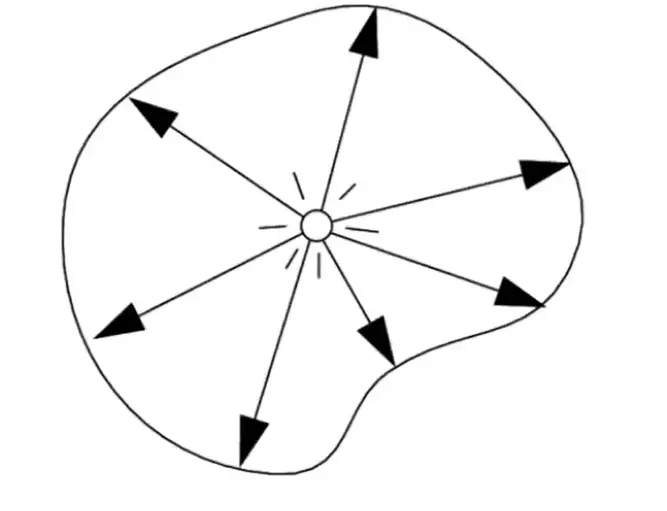
angles and solid andgles

• \(\theta=\frac{l}{r}\) 弧长除以半径
• \(\Omega =\frac{A}{r^2}\) 面积除以半径平方
• 微分立体角，整个球的立体角为 \(4\pi\)
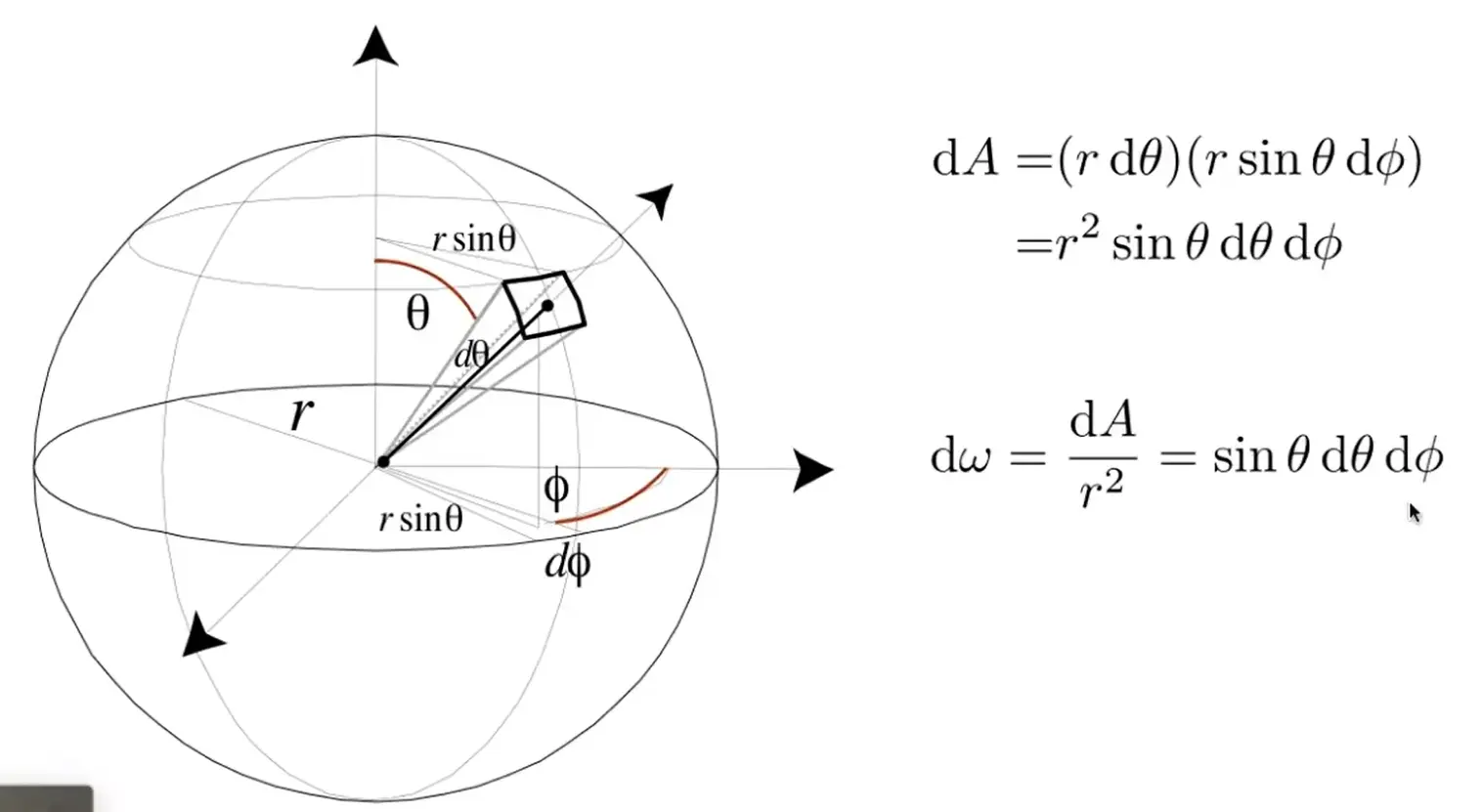
• 后面会用 \(\omega\) 来表示一个单位长度的方向向量

对于一个向所有方向均匀辐射的点光源，\(I=\frac{\Phi}{4\pi}\)

Irradiance: power per unit area

\[E(\mathbf{x})\equiv\frac{\mathrm{d}\Phi(\mathbf{x})}{\mathrm{d}A}\left[\frac{\mathrm{W}}{\mathrm{m}^{2}}\right]\left[\frac{\mathrm{lm}}{\mathrm{m}^{2}}=\mathrm{lux}\right]\]

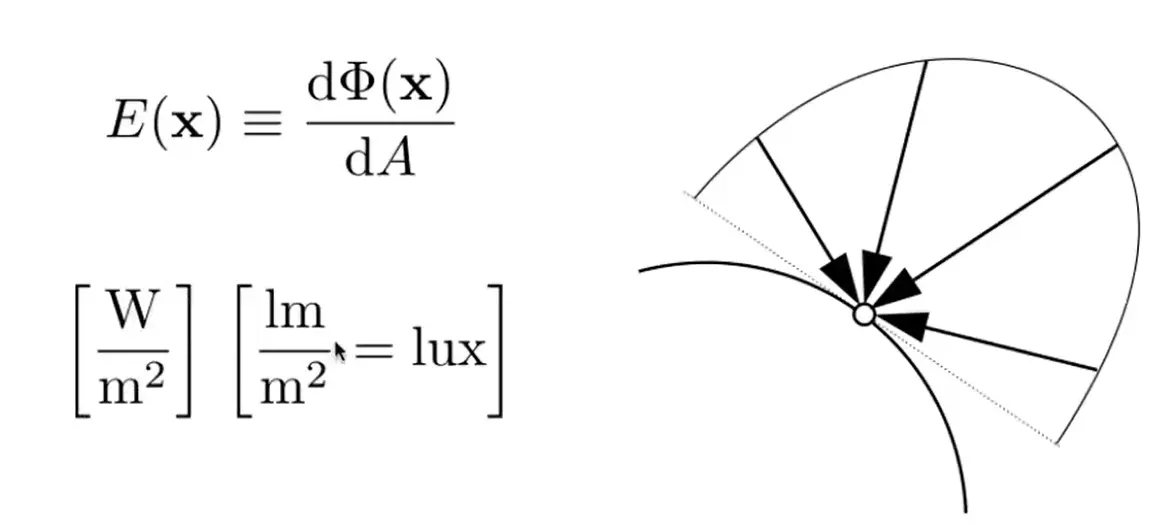
Note

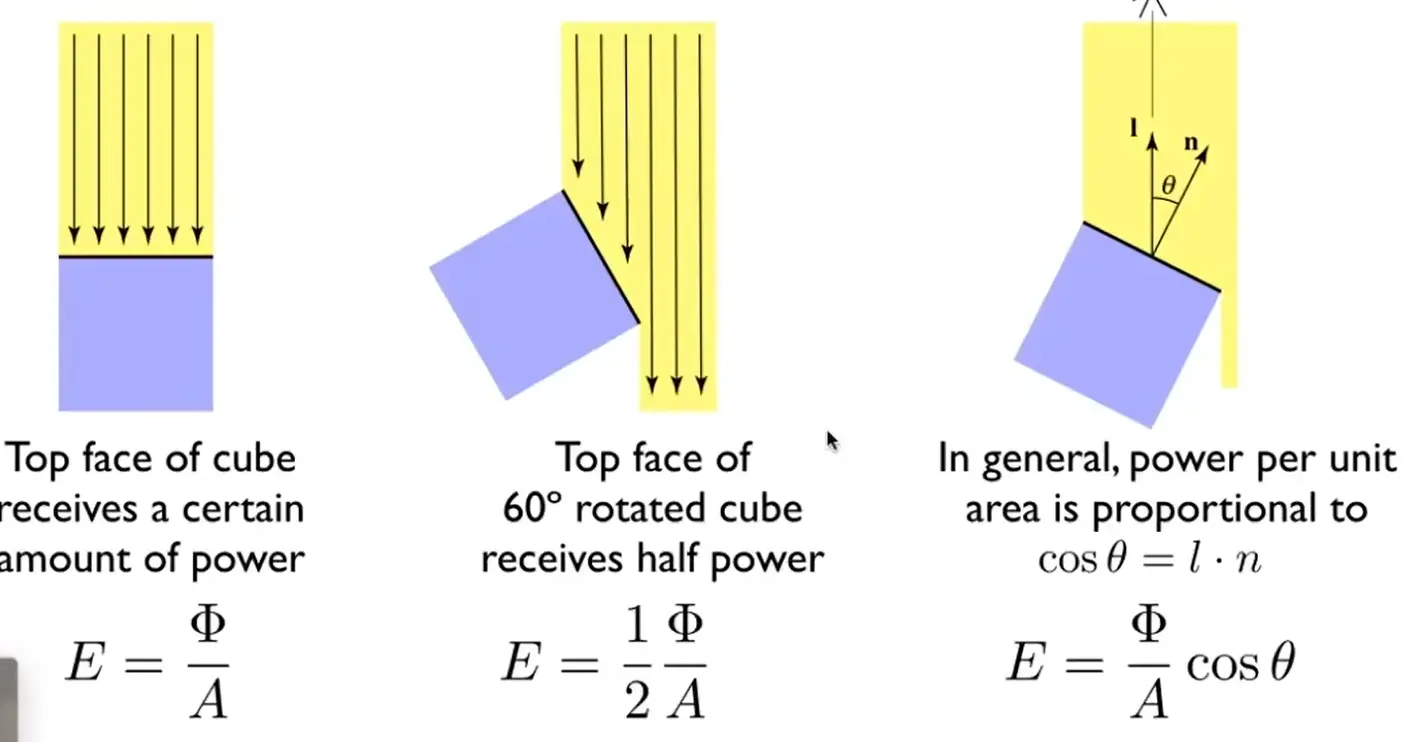
需要考虑 cosine law

Note

回忆平方反比，其实 intensity(单位立体角上的功率) 没有衰减，是 irradiance(单位面积接收能量) 在衰减

Radiance(Luminance): power per unit solid angle, per projected unit area

\[L(\mathrm{p},\omega) \equiv\frac{\mathrm{d}^2\Phi(\mathrm{p},\omega)}{\mathrm{d}\omega \mathrm{d}A\cos\theta} \left[\frac{\mathrm{W}}{\mathrm{sr} \mathrm{m}^2}\right]\left[\frac{\mathrm{cd}}{\mathrm{m}^2}=\frac{\mathrm{lm}}{\mathrm{sr} \mathrm{m}^2}=\mathrm{nit}\right]\]

Note

下面的 cos 表示 \(\omega\) 方向上的投影面积

Tip

• 一次微分
  • Irradiance: power per projected unit area
  • Intensity: power per solid angle
• 两次微分
  • Radiance: Irradiance per solid angle
  • Radiance: Intensity per projected unit area

Exiting Radiance: 和 Radiance 一样，但是发出的能量

\[L(\mathrm{p},\omega)=\frac{\mathrm{d}I(\mathrm{p},\omega)}{\mathrm{d}A\cos\theta}\]

Irradiance vs. Radiance

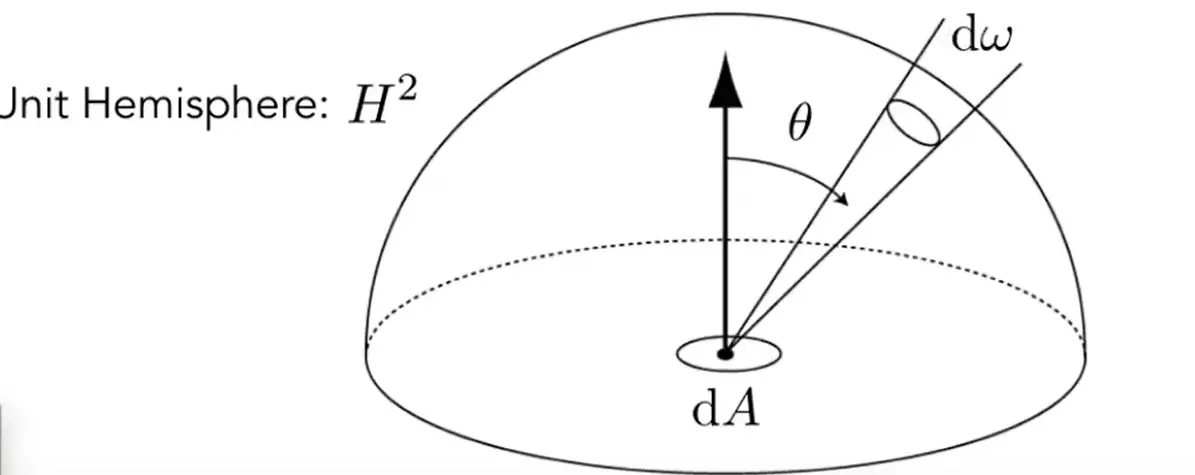
• Irradiance: 面积微元 \(\mathrm{d}A\) 上接收的总能量
• Radiance: 面积微元 \(\mathrm{d}A\) 从 \(\mathrm{d}\omega\) 方向上接收到的能量

\[\begin{aligned} dE(\mathrm{p},\omega) & =L_i(\mathrm{p},\omega)\cos\theta\mathrm{d}\omega \\ E(\mathrm{p}) & =\int_{H^2}L_i(\mathrm{p},\omega)\cos\theta\mathrm{d}\omega \end{aligned}\]

Bidirectional Reflectance Distribution Function (BRDF)

双向反射分布函数 从 \(\omega_{i}\) 来的 Radiance 打到 \(\mathrm{d}A\) 上，能量 \(E\) 转化到反射光线中，给出了反射光线的分布

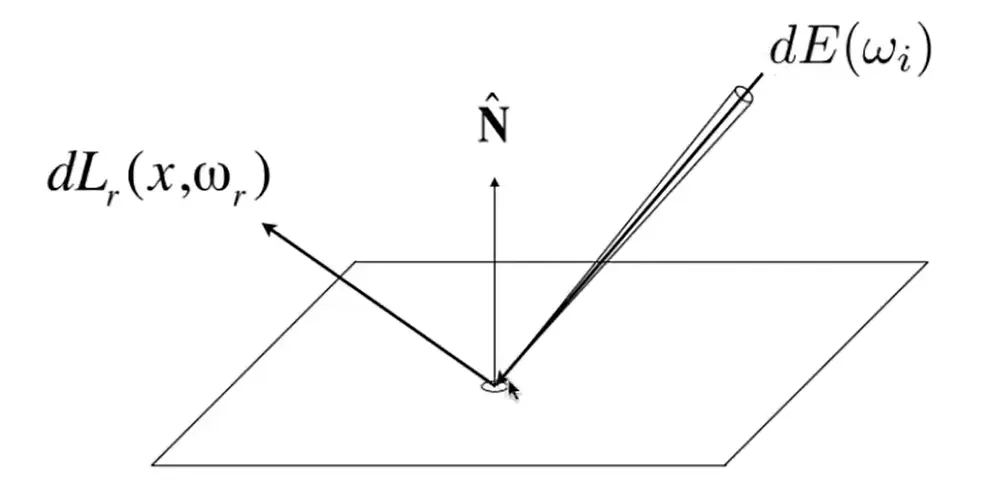
• differential irradiance incoming (入射 irradiance): \(\mathrm{d}E(\omega_{i})=L(\omega_{i})\cos \theta_{i}\mathrm{d}\omega_{i}\)
• differential radiance exiting (due to \(\mathrm{d}E(\omega_{i})\)): \(\mathrm{d}L_{r}(\omega_{r})\)

\[\text{BRDF: }f_r(\omega_i\to\omega_r)=\frac{\mathrm{d}L_r(\omega_r)}{\mathrm{d}E_i(\omega_i)}=\frac{\mathrm{d}L_r(\omega_r)}{L_i(\omega_i)\cos\theta_i\mathrm{d}\omega_i}\left[\frac{1}{\text{sr}}\right]\]

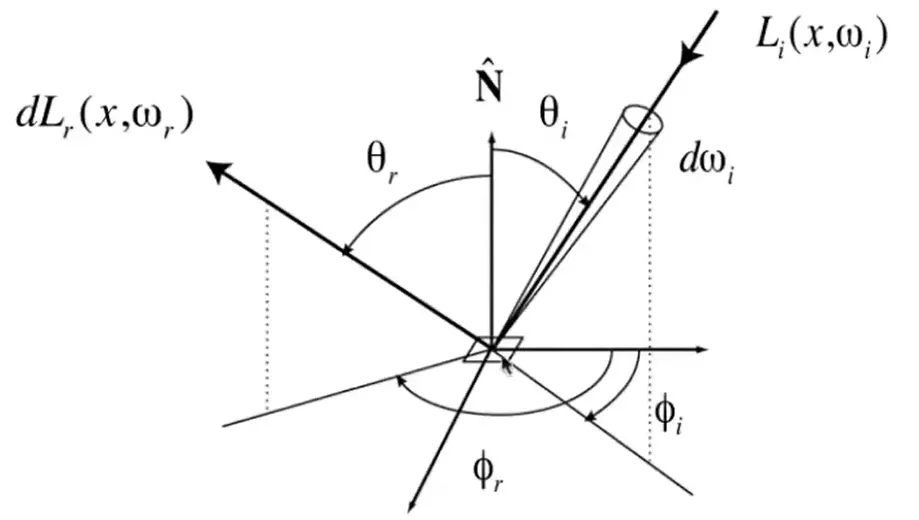
Note

将漫反射和镜面反射一起考虑

The Reflection Equation

\[\text{The Reflection Equation: }L_r(\mathrm{p},\omega_r)=\int_{H^2}f_r(\mathrm{p},\omega_i\to\omega_r)L_i(\mathrm{p},\omega_i)\cos\theta_i\mathrm{d}\omega_i\]

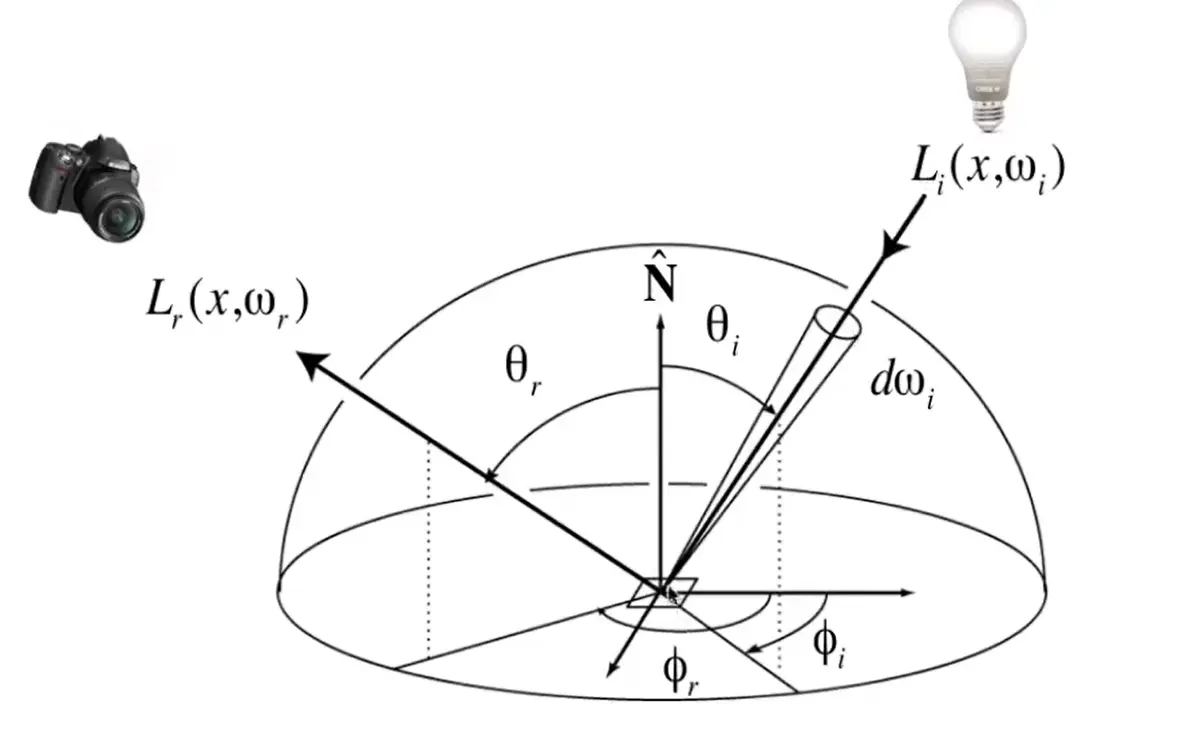
Note

将所有可能的入射方向积分，得到观测方向的能量

challenge: recursive equation

光线可能弹射多次，一个面积微元的入射光可能来自另一个面积微元

The Rendering Equation

考虑物体本身的发光，重写 reflection eqation

\[\text{The Rendering Equation: }L_o(p,\omega_o)=\underbrace{ L_e(p,\omega_o)}_{\text{emitted by the object itself}}+\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot\omega_i)\mathrm{d}\omega_i\]

Note

• 假设所有的向量都是向外的
• \(\cos \theta=n\cdot w_{i}\)

进行简化：

\[ \begin{align} \to && l(u)&=e(u)+\int l(v)K(u,v)dv \\ \to && L&=E+KL \end{align} \]

这里的 \(L\) 是全局光照(Global Illimination)

\[ \begin{align} L&=E+KL \\ (I-K)L&=E \\ L&=(I-K)^{-1}E \\ L&=(I+K+K^2+K^3+\dots)E \\ L&=E+KE+K^2E+K^3E+\dots \end{align} \]

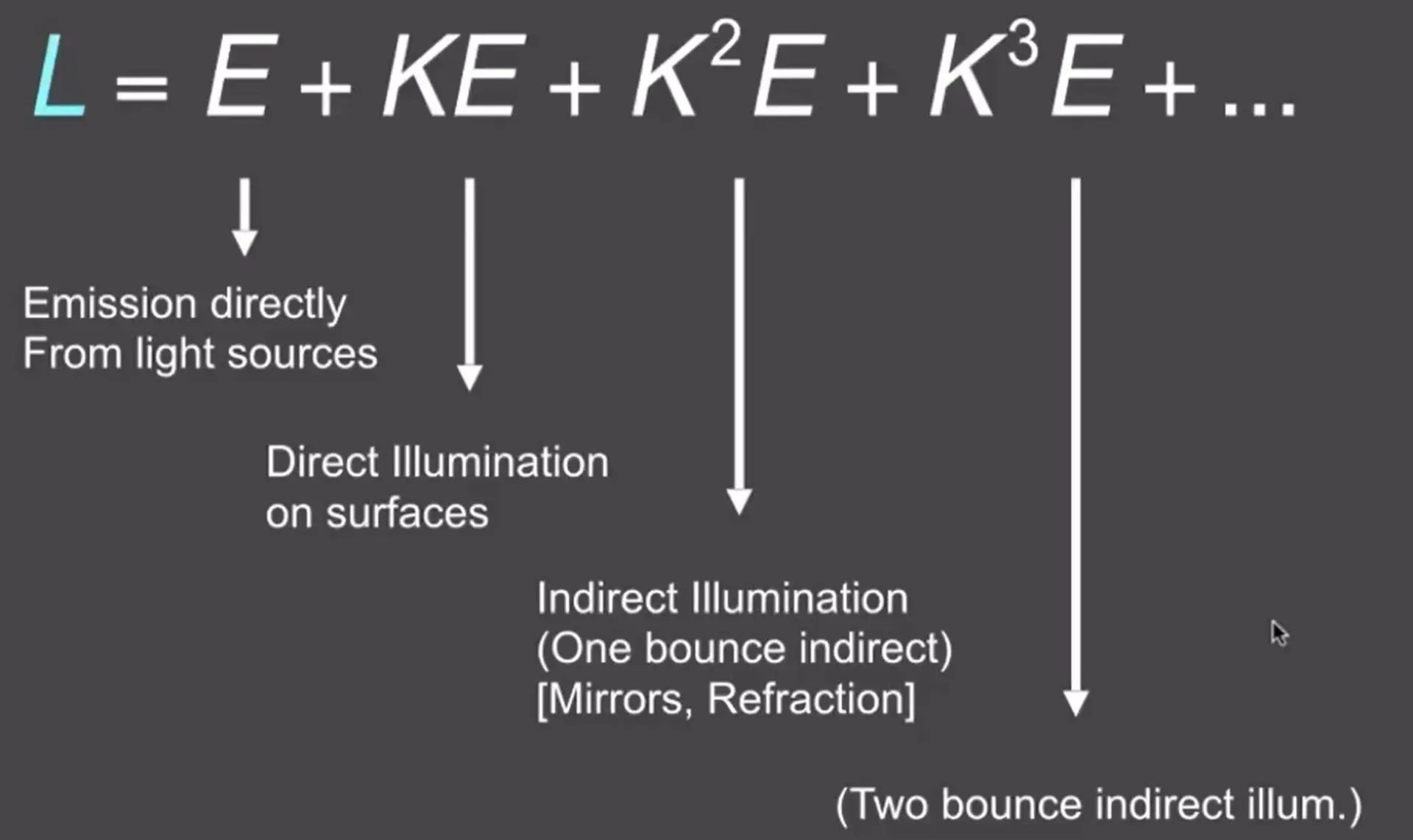
Note

• 光线弹射0、1、2、... 次得到的光照
• rasterization 最多考虑了一次弹射(direct illumination)，也就是 \(E+KE\)
• 考虑无限次光线弹射，最终亮度会收敛

Path Tracing

Whitted-Style recap: 不准确的估计

• 遇到光滑面，考虑镜面反射光线
• 遇到漫反射面，不考虑反射光线

Monte Carlo Integration

why

we want to solve an integral, but it can be too difficult to solve analytically.

对于定积分 \(\int_{a}^b f(x)\mathrm{d}x\)，取随机变量 \(X_i\sim p(x)\)，则 Monte Carlo Integration 为：

\[\int f(x)\mathrm{d}x\approx\frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)}\]

一种特殊情况是平均分布 \(X_{i}\sim p(x)=\frac{1}{b-a}\)：

\[F_N=\frac{b-a}{N}\sum_{i=1}^Nf(X_i)\]

Note

• 采样越多，方差越小
• 在 x 上积分，就在 x 上采样

Solve Rendering Equation

\[\text{The Rendering Equation: }L_o(p,\omega_o)=\underbrace{ L_e(p,\omega_o)}_{\text{emitted by the object itself}}+\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot\omega_i)\mathrm{d}\omega_i\]

challenge

• 在半球面上积分
• recursive execution

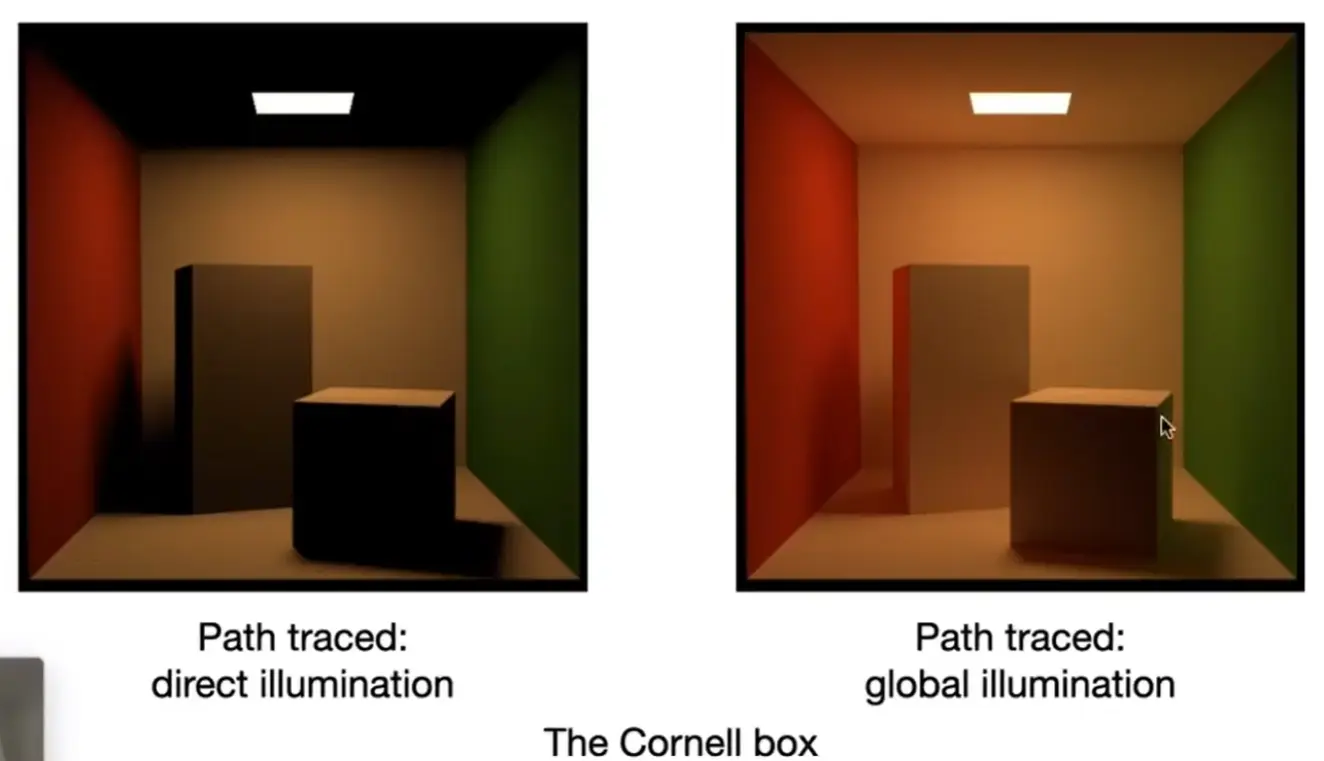
Direct Illumination

考虑要渲染一个像素(pixel, point)的 direct illumination

\[L_o(p,\omega_o)=\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot\omega_i)\mathrm{d}\omega_i\]

使用 Monte Carlo 进行采样

\[ \begin{align} f(x)\text{ in Monte Carlo} & =L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot\omega_i) \\ p(\omega_{i})\text{ in Monte Carlo}&=1/2\pi \end{align} \]

得到

\[\begin{aligned} L_{o}(p,\omega_{o}) & =\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot\omega_i)\mathrm{d}\omega_i \\ & \approx\frac{1}{N}\sum_{i=1}^N\frac{L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot\omega_i)}{p(\omega_i)} \end{aligned}\]

shade(p, wo)
    Randomly choose N directions wi~pdf(w)
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)

Global Illumination

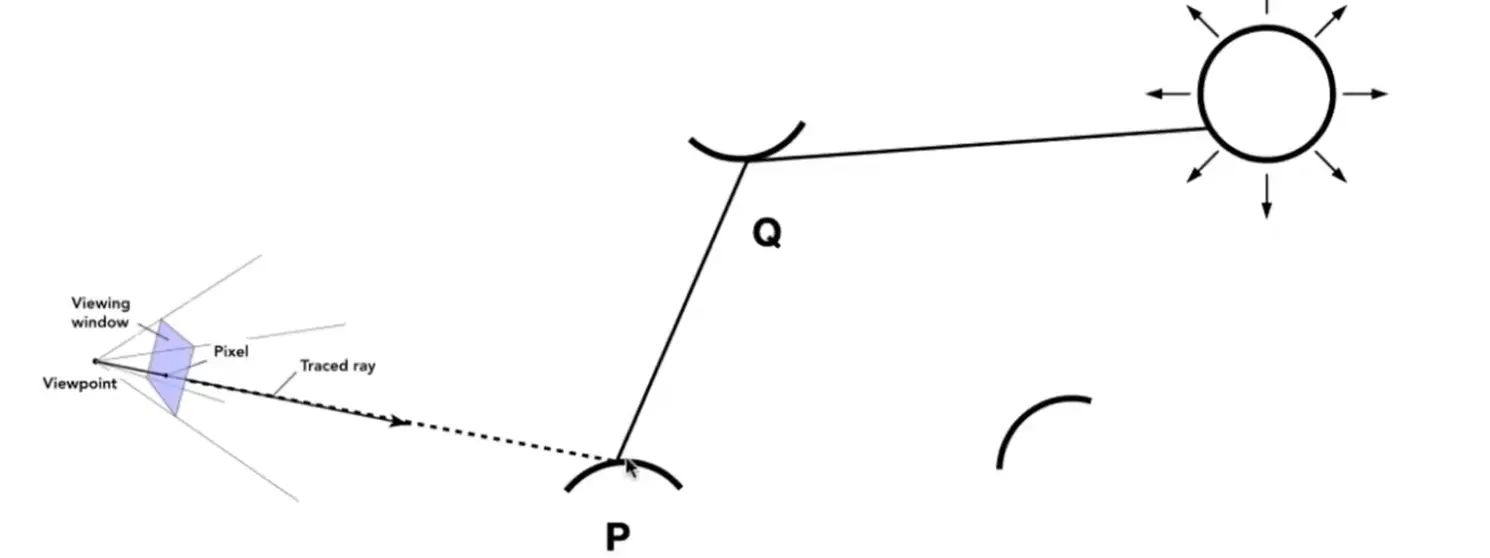
递归特性

Q 反射到 P 的光线，相当于从 P 点看 Q 点的 direct illumination

shade(p, wo)
    Randomly choose N directions wi~pdf(w)
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
        Else If ray r hit an object at q:
            Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi)
    Return Lo

Path Tracing

done? NO

• 光线数量爆炸 \(\#\text{rays}=N^{\#\text{bounces}}\)
• 只有 \(N=1\) 的时候，不会爆炸

shade(p, wo)
    Randomly choose ONE directions wi~pdf(w)
    Trace a ray r(p, wi)
    If ray r hit the light
        Return L_i * f_r * cosine / pdf(wi)
    Else If ray r hit an object at q:
        Return shade(q, -wi) * f_r * cosine / pdf(wi)
    Return Lo

Note

Path Tracing 就是 \(N=1\) 的情况，如果 \(N\neq 1\)，称为 Distributed Ray Tracing

Problem 1: Noise Control

too noisy?

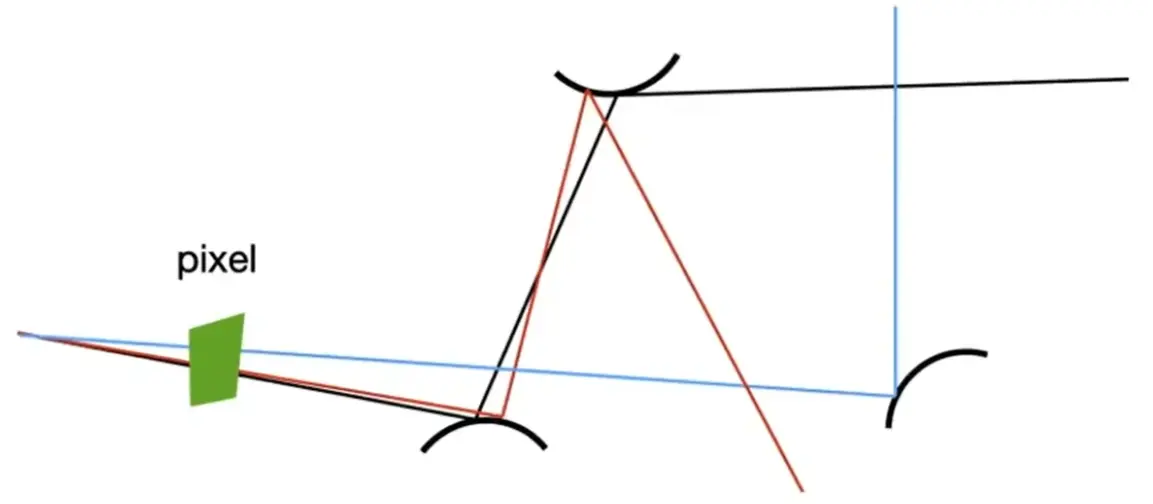
multiple paths，求平均

ray_generation(camPos, pixel)
    Uniformly choose N sample positions within the pixel
    pixel_radiance = 0.0
    For each sample in the pixel
        Shoot a ray r(camPos, cam_to_sample)
        If ray r hit the scene at p
            pixel_radience += 1 / N * shade(p, sample_to_cam)
    Return pixel_radiance

Problem 2: Recursion

Russian Roulette (RR)

• with probability \(0<p<1\), continue
• with probability \(1-p\), stop
• 期望进行 \(\frac{1}{1-p}\) 次

• 一个点接收到一个光线后：
  • 以 \(p\) 的概率继续发射光线追踪，得到 \(L_{o}/p\) （人为除以 \(p\)）
  • 以 \(1-p\) 的概率不追踪，得到 \(0\)
  • 那么期望是 \(E=p \cdot (L_{o}/p)+(1-p)\cdot 0=L_{o}\)，期望与真实值一样！

shade(p, wo)
    Manually specify a probability P_RR
    Randomly select ksi in a uniform dist. in [0, 1]
    If (ksi > P_RR) Return 0.0

    Randomly choose ONE directions wi~pdf(w)
    Trace a ray r(p, wi)
    If ray r hit the light
        Return L_i * f_r * cosine / pdf(wi) / P_RR
    Else If ray r hit an object at q:
        Return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR
    Return Lo

Advanced Problem: Path Tracing is not efficient

Note

SPP(samples per pixel) 足够大，效果才能好，但是效率会变低

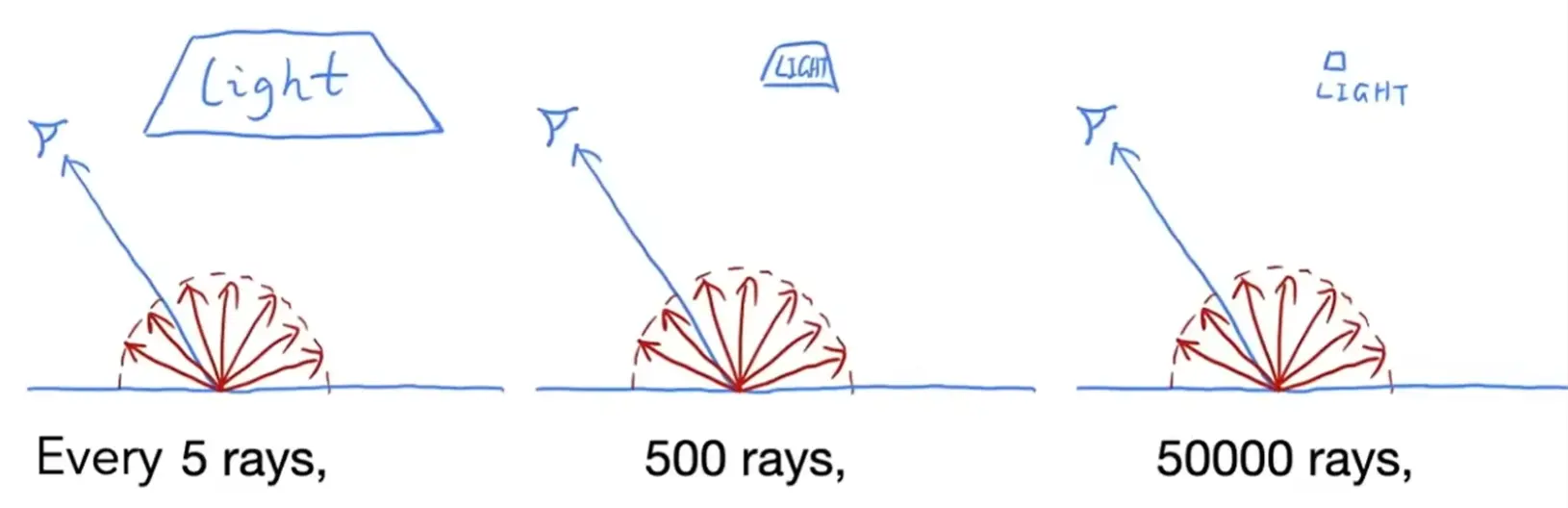
Note

• 光源大的时候，并不需要太多光线
• 光源小的时候，需要很多光线
• 均匀向所有方向采样，会造成浪费，需要用非均匀的 PDF

Sampling the light

如何实现对光源采样？

• 渲染方程在半球上积分，光源采样在光源 \(A\) 上积分 \(p=1/A\)
• 需要找到 \(A\) 和 \(\omega\) 的关系找到，将 Monte Carlo 写成在 \(A\) 上采样

根据立体角关系得到：

\[d\omega=\frac{dA\cos\theta^{\prime}}{\|x^{\prime}-x\|^2}\]

改变积分域：

\[\begin{aligned} L_o(x,\omega_o) & =\int_{\Omega^+}L_i(x,\omega_i)f_r(x,\omega_i,\omega_o)\cos\theta\mathrm{d}\omega_i \\ & =\int_AL_i(x,\omega_i)f_r(x,\omega_i,\omega_o)\frac{\cos\theta\cos\theta^{\prime}}{\|x^{\prime}-x\|^2}\mathrm{d}A \end{aligned}\]

light source v.s. other

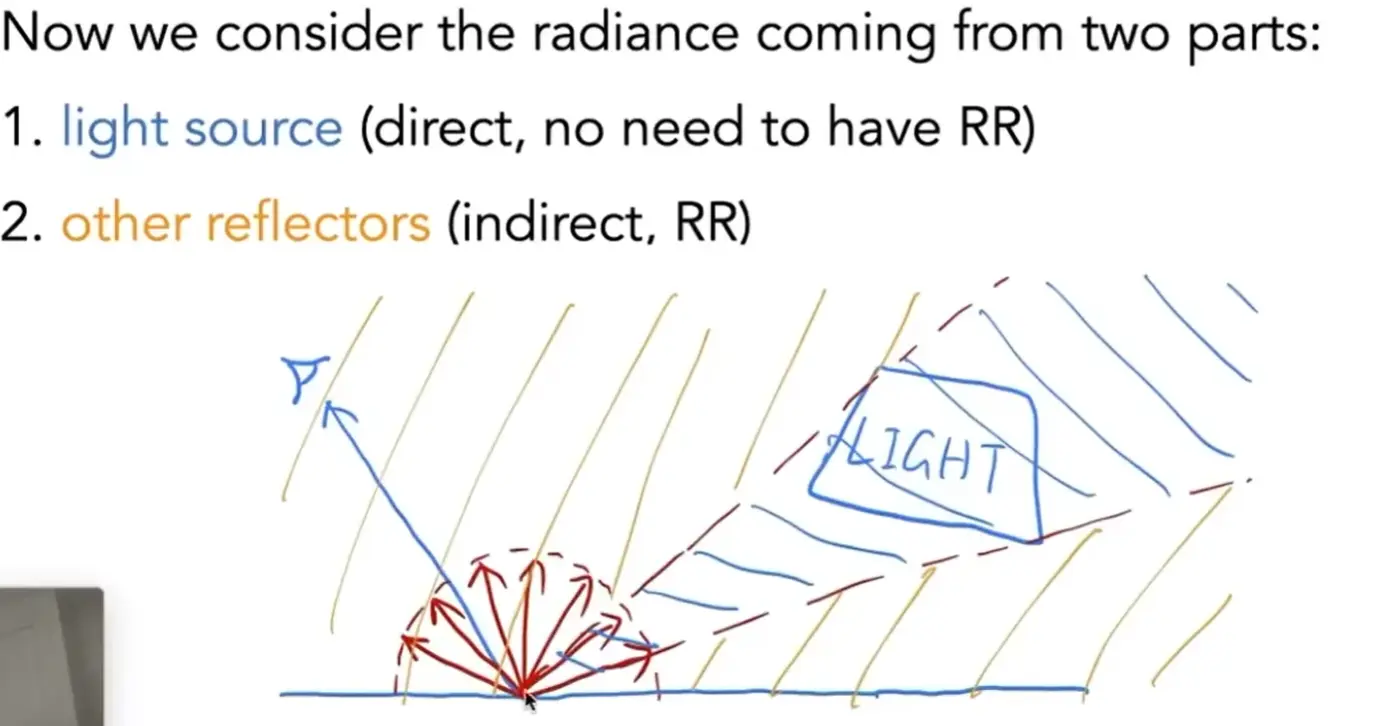
分成两部分考虑

• 光源部分直接在光源上采样，不用使用 RR
• 其他部分仍然使用 RR

shade(p, wo)
    # Contribution from the light source.
    L_dir = 0.0
    Uniformly sample the light at x' (pdf_light = 1 / A)
    Shoot a ray from p to x'
    If the ray is not blocked in the middle
        L_dir = L_i * f_r * cos theta * cos theta' / |x'-p| ^ 2 / pdf_light

    # Contribution from other reflections
    L_indir = 0.0
    Test Russian Roulette with probability P_RR
    Uniformly sample the hemishpere toward wi (pdf_hemi = 1 / 2pi)
    Trace a ray r(p, wi)
    If ray r hit a non-emiting object at q
        L_indir = shade(q, -wi) * f_r * cos theta / pdf_hemi / P_RR

    Return L_dir + L_indir

Important

注意光源采样时，要保证光源不被遮挡

Outro

• Path Tracing is PHOTO-REALISTIC
• Ray tracing: Previous v.s. Modern Concepts
  • previous
    • ray tracing == Whitted-style ray tracing
  • modern
    • The general solution fo light transport
    • path tracing
    • photon mapping
    • ...
• how to uniformly sample the hemisphere?
• what's the best pdf?
• random number matters(low discrepancy sequences)
• 结合 hemishpere 和 light 两种采样方法，可以得到更好的效果
• radiance 不是 color，需要经过 gamma correction 才能得到 rgb color

Comments