04 Resterization

Perspective Projection Cont.

near plane

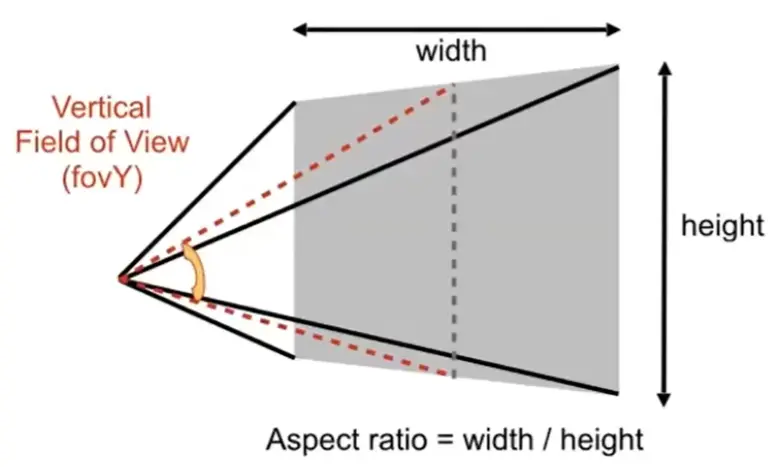
• width, height, aspect ratio
• field of view: vertical (fovY), horizontal (fovX)
• 通常，取原点对称

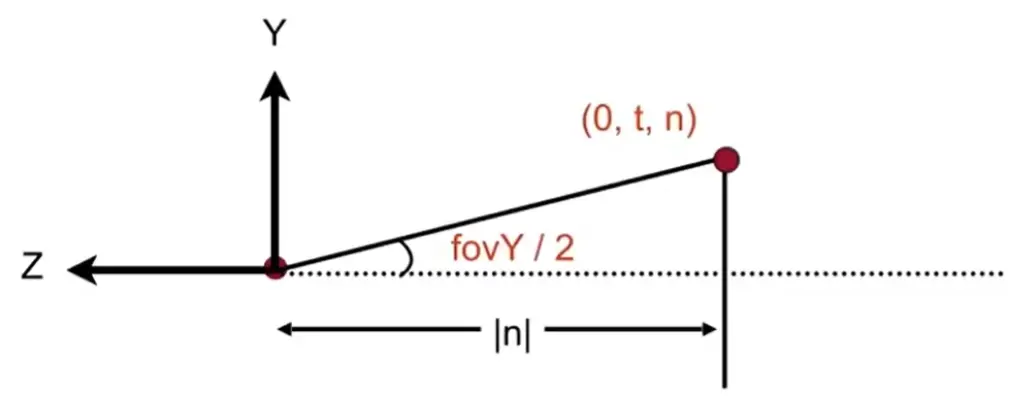
• \(\tan\frac{fovY}{2}=\frac{t}{|n|}\)
• \(\text{aspect}=\frac{r}{t}\)

Canonical Cube to Screen

screen

• an array of pixels
• resolution
• a typical raster display

pixel

• r g b
• 定义左下角是原点，向右是 X，向上是 Y
• pixel \((x,y)\) is centered at \((x+0.5,y+0.5)\)

projection

xy coordinates: \([-1,1]^2\) to \([0,\text{width}]\times[0,\text{height}]\), viewpoint transformation

\[M_{viewport}= \begin{pmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} \\ 0 & \frac{height}{2} & 0 & \frac{height}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]

Rasterization

raster displays

• 阴极射线管：逐行扫描、隔行扫描
• Frame Buffer: pixel arrays in memory

a simple approach: sampling

使用像素中心对模型进行采样，判断一个像素的中心是否在三角形内部

for (int x = 0; x < xmax; ++x)
    for (int y = 0; y < ymax; ++y)
        image[x][y] = inside(tri, x + 0.5, y + 0.5);

实现 inside()

• 进行向量叉积，从判断 \(\vec{P_{0}P}\) 和 \(\vec{P_{0}P_{1}}\) 的位置关系开始，在三条边的同侧则在三角形内部
• 刚好在三角形边上时，可以规定其属于左边或上边

bounding box

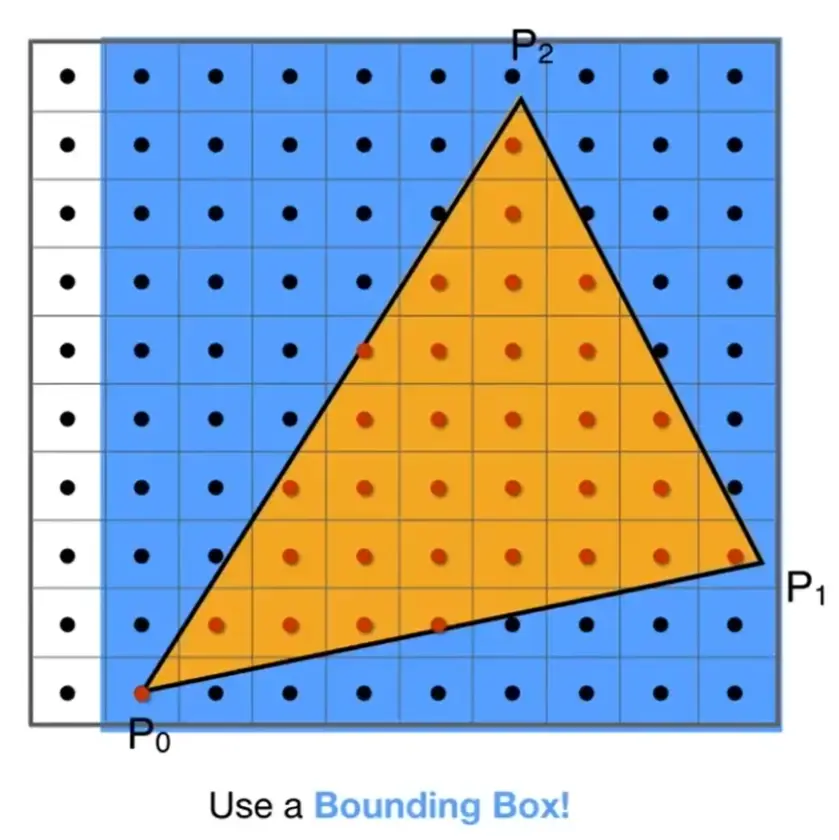
• 只有 bounding box 中的像素点才需要考虑

Question

采样精度小的时候，容易产生锯齿

Antialiasing

recap: 锯齿，走样

intro

• sampling artifacts
  • jaggies - sampling in space
  • moire patterns - undersampling images
  • false motion - sampling in time
• 信号的变化太快，跟不上采样速度

idea: blurring(pre-filtering) before sampling

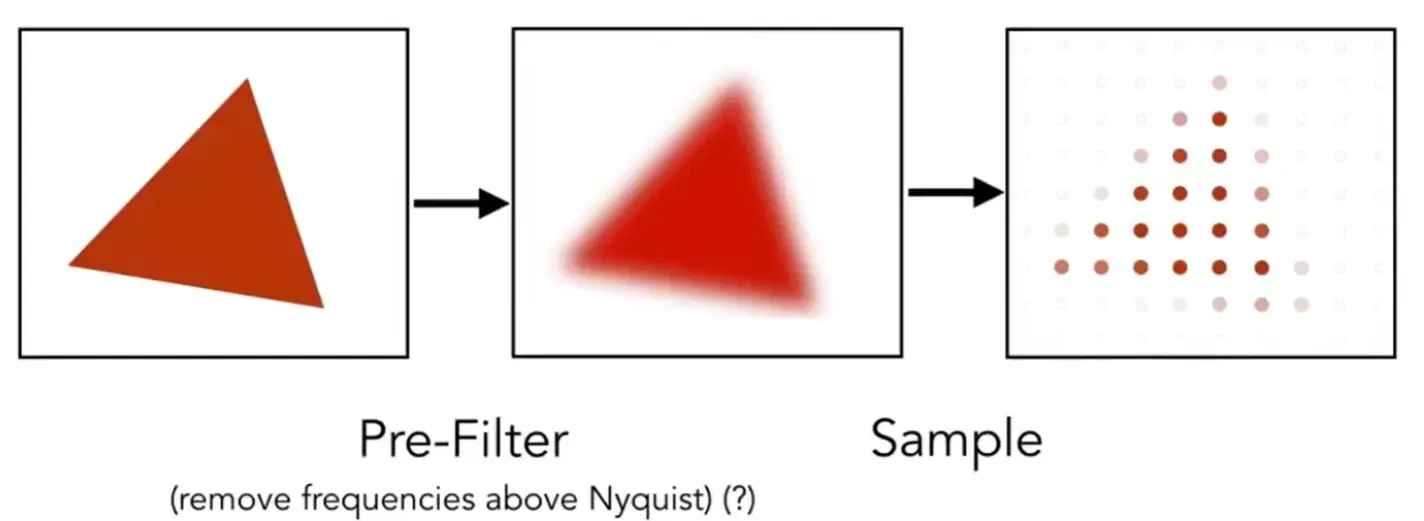
Warning

一定是 filter then sample，不能用 sample then filter，否则效果会更差

Frequncy Domain 频域

intro

• \(f=\frac{1}{T}\)
• Fourier Transform: spatial domain (时域) -> frequency domain (频域)
• 频率高，需要的采样频率也更高

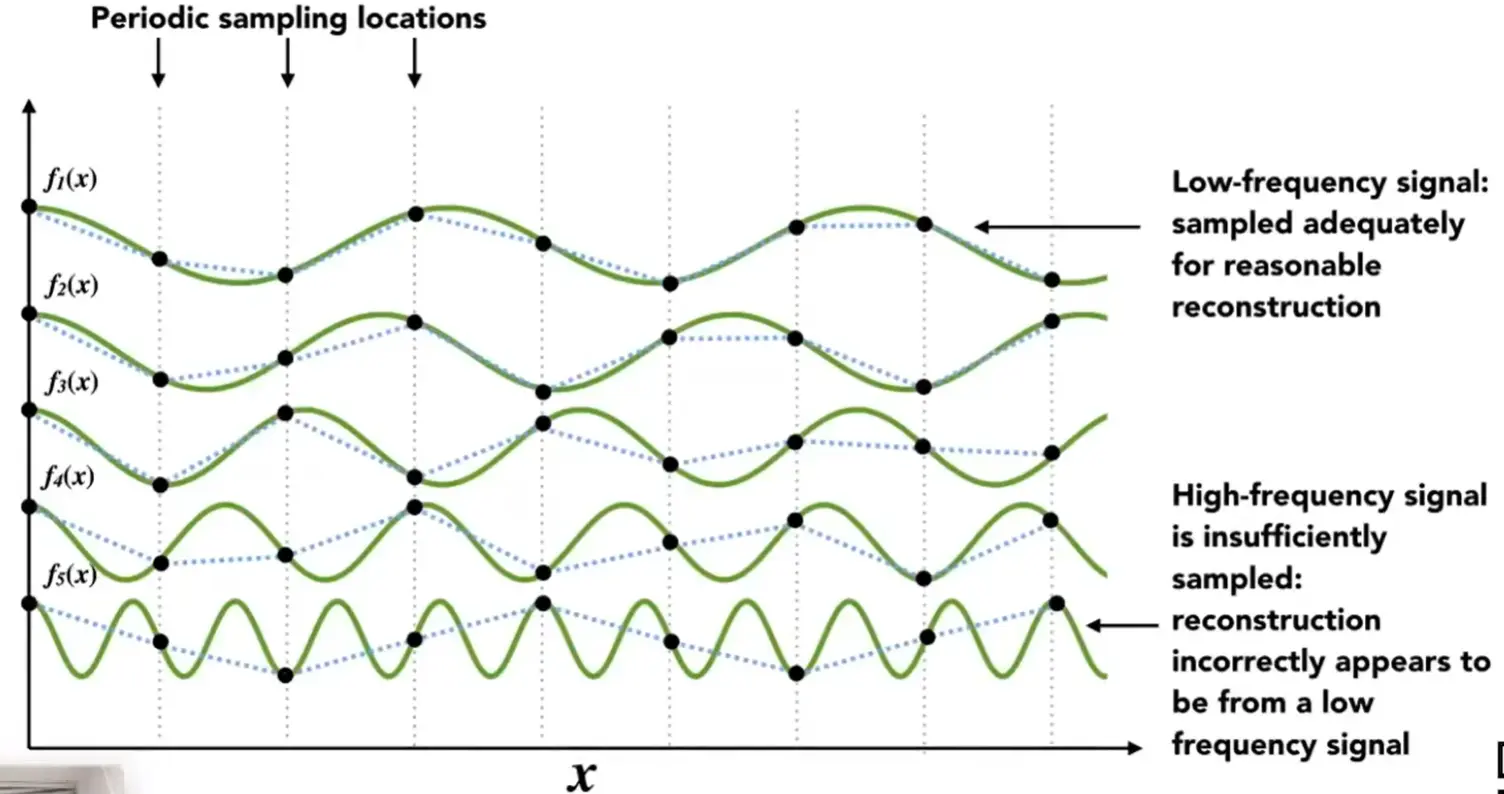
Aliases

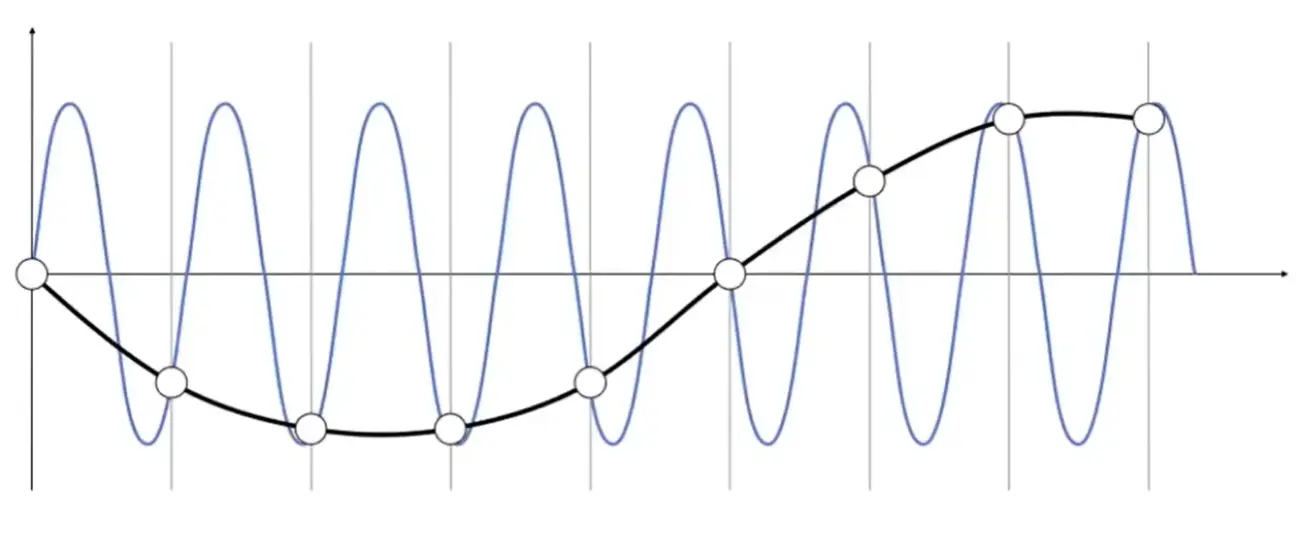
高频信号经过 undersampling 得到的结果失真（和某种低频信号产生相同的结果）

Filtering

about high/low freq.

= Getting rid of certain freq. contents 去掉一系列频率

右侧是频域可视化

• 中间为低频，说明低频信息比较丰富
• 可以忽略水平和竖直的两条线

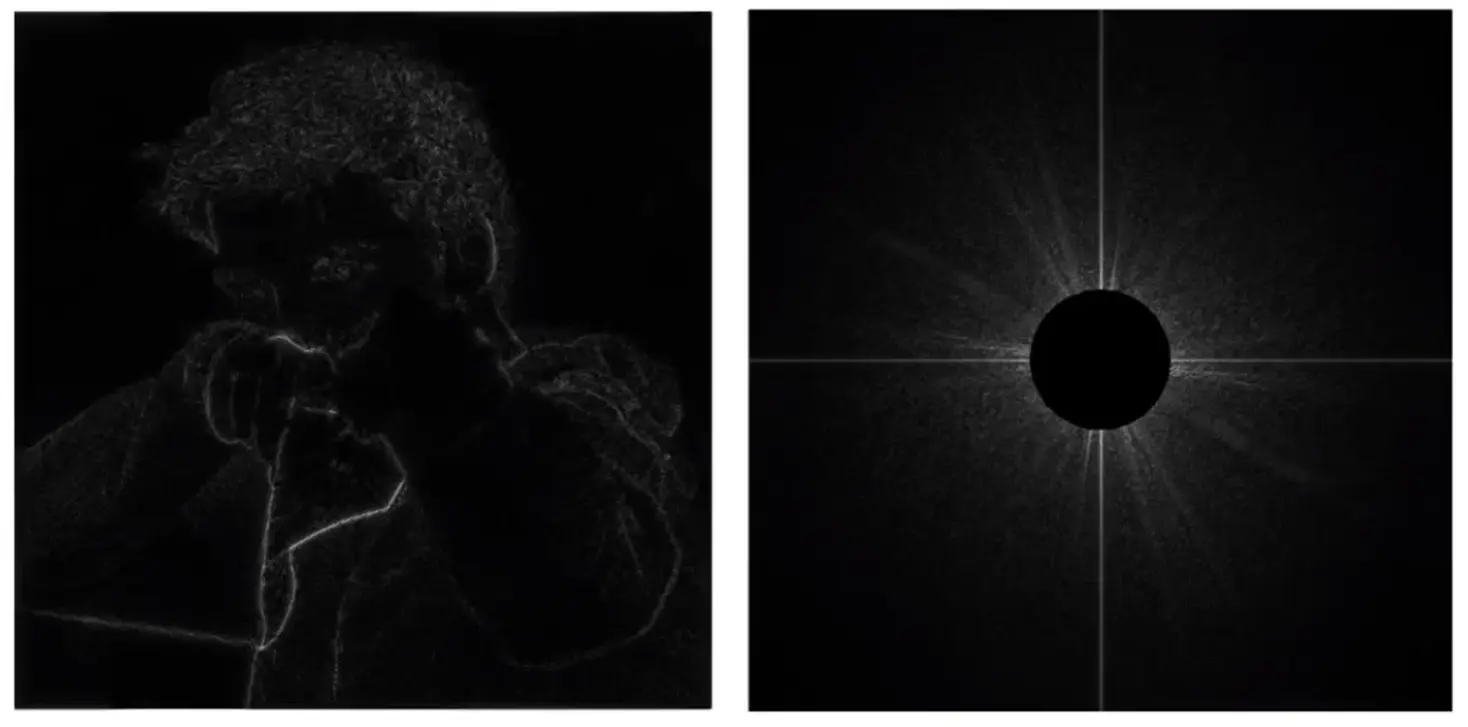
Note

• 高频信息对应图像的边界
• 低频信息对应图像内部平滑的部分

with convolution

= Average = Convolution

• Convolution in the spactial domain is equal to multiplication in the freq. domain, and vice versa
  • option1: filter by convolution in spatial doamin
  • option2:
    • transform to freq. domain (Fourier)
    • multiply by Fourier transform of convolution kernel
    • transform back to spatial domain (inverse Fourier)

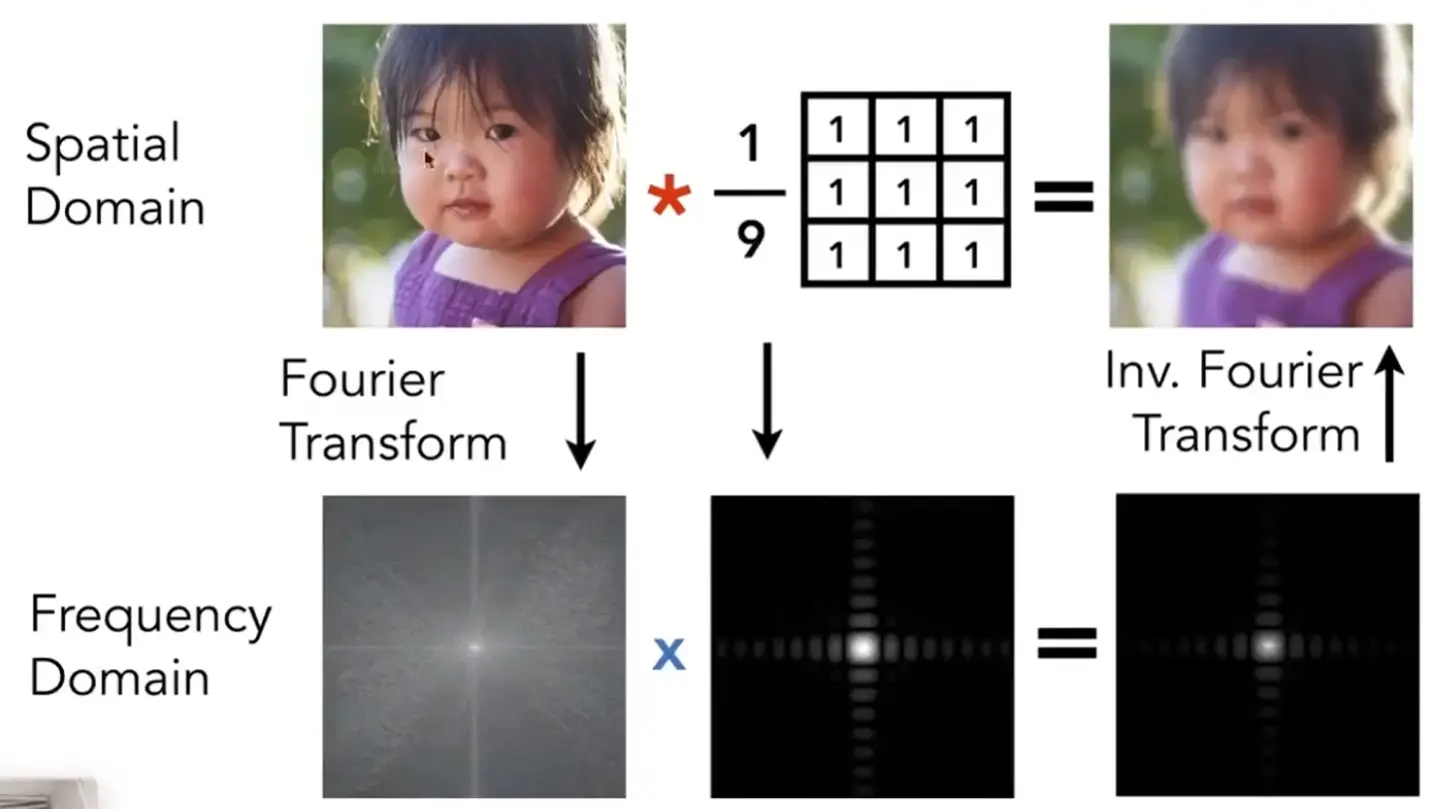
Note

卷积核越大，得到的图像越平滑，频域越低

Sampling

= repeating freq. contents，就是在复制

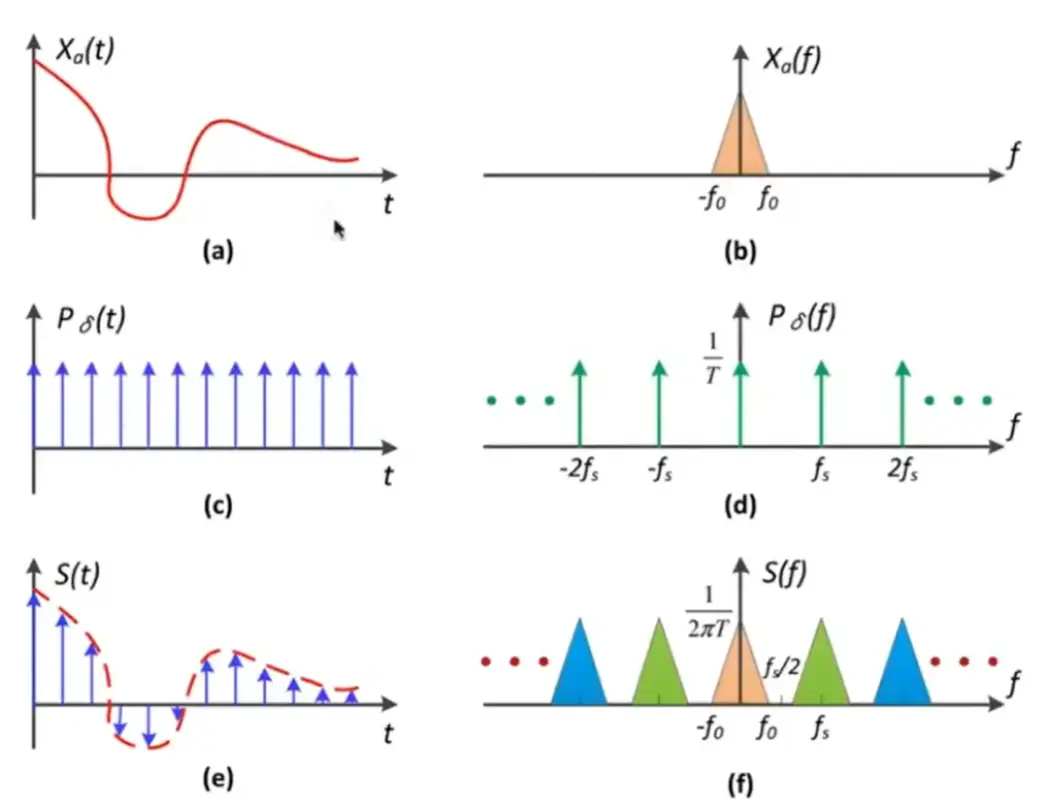
Note

• 左图中的箭头是冲击函数，对应采样点
• 频域上的来看就是卷积，将原有的频谱复制了很多份
• 时域上的乘积对应频域上的卷积

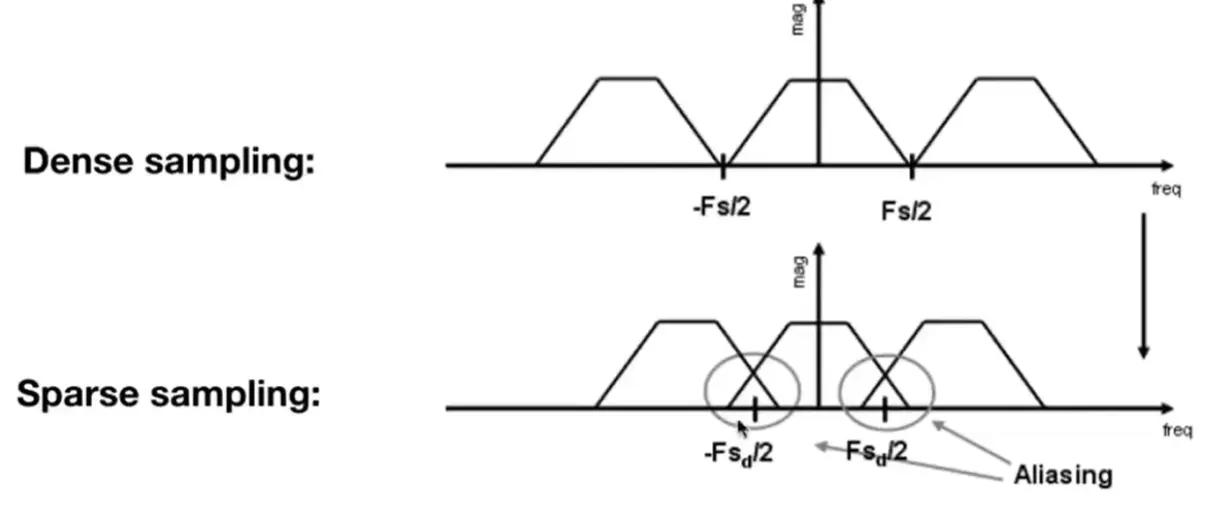
Note

• 采样越稀疏，频谱越密集，会产生混叠，导致 aliasing

Antialiasing

• option1: 提高采样率 costly
• option2: antialiasing

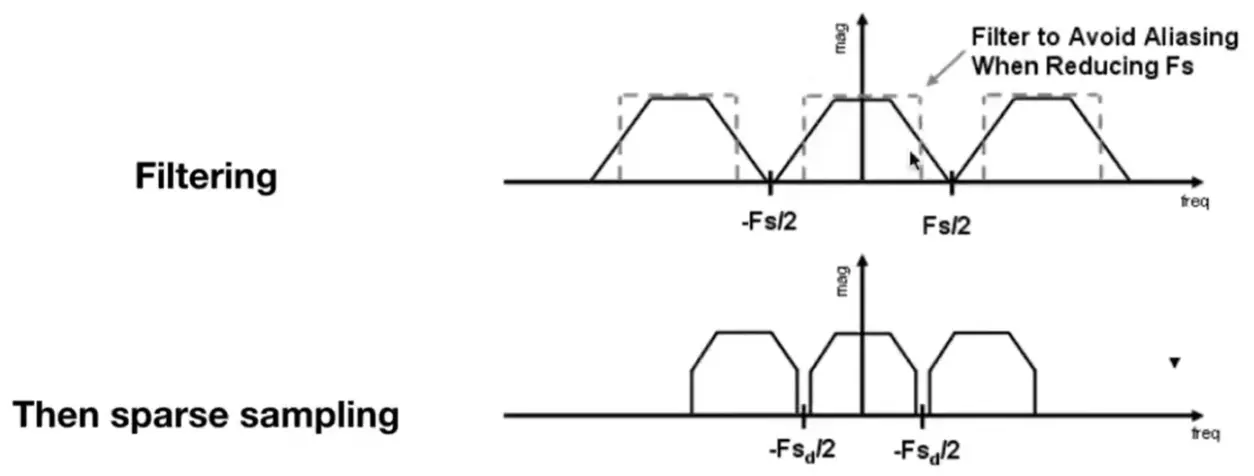
Note

减少高频信号，在采样率低时也不会产生混叠

solution: computing average pixel value

• convolve: 每个像素取平均值
• sampling: 对每个像素中心进行采样

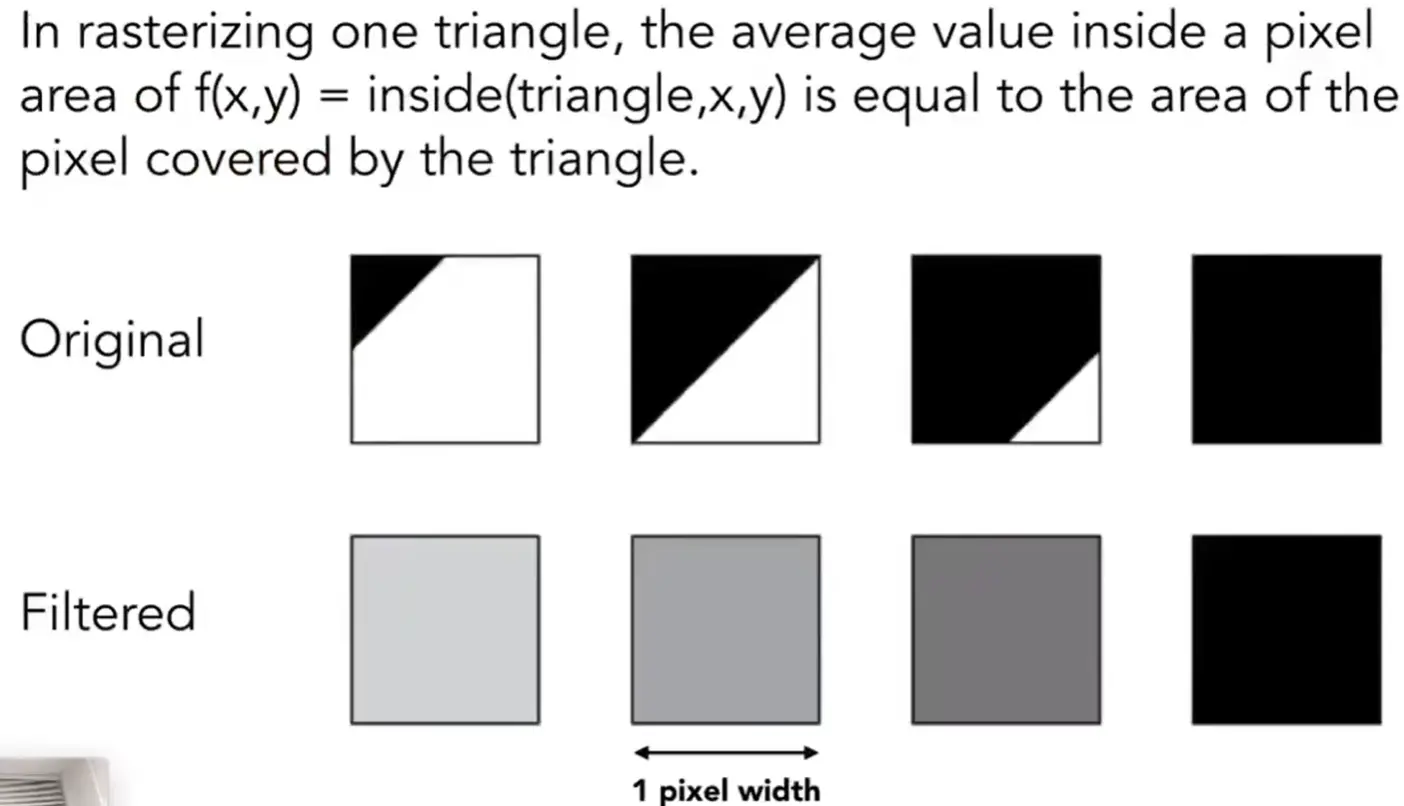
practice: by supersampling (MSAA)

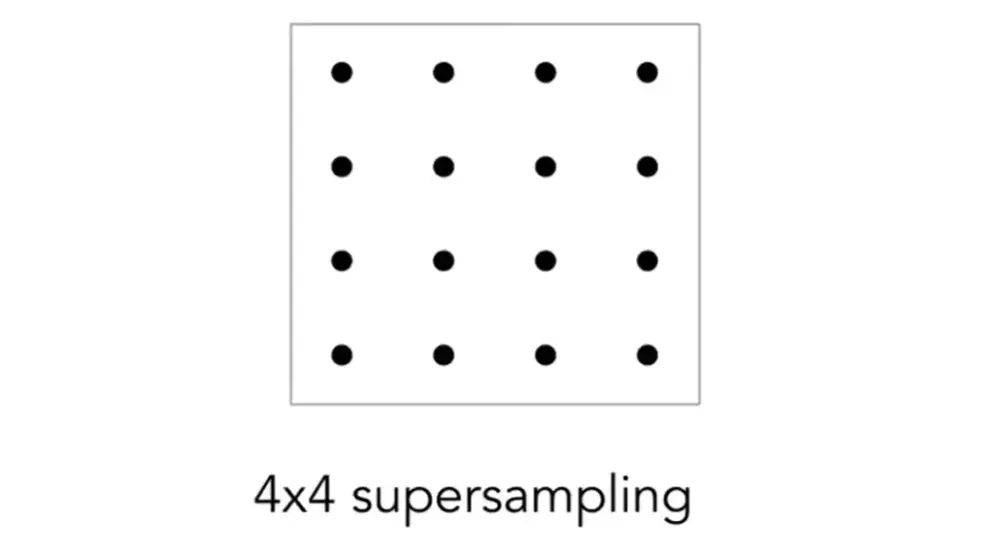
• 每个像素内部选多个采样点，并取平均

Antialiasing today

• 使用不规则采样点分布来减少计算量
• 其他的抗锯齿方法
  • FXAA(Fast Approximate AA) 将有锯齿边替换为无锯齿边
  • TAA(Temporal AA) 复用上一帧的结果
• 超分辨率 super resolution
  • resolution low to high，会导致锯齿
  • DLSS(Deep Learning Super Sampling)

Visibility/Z-Buffering

Painter's Algorithm

• 先画出远的物体，再画出近的物体
• 不需要考虑遮挡关系，\(O(n\log n)\)
• 可能无法进行排序互相遮挡

Z-Buffer 深度缓冲

保存一个像素当前最浅的深度

For simplicity we suppose

• z is always positive
• smaller z -> closer

for (each triangle T)
    for (each sample (x, y, z) in T)
        if (z < z_buffer(x, y))
            frame_buffer(x, y) = rgb;
            z_buffer = z;

• \(O(n)\)
• 不同顺序绘制的结果是一样的
• 在 GPU 中硬件实现
• 透明物体不适用

Shadows

Shadow Mapping

如果视野中的一个点能被光源看到，那么就有光照

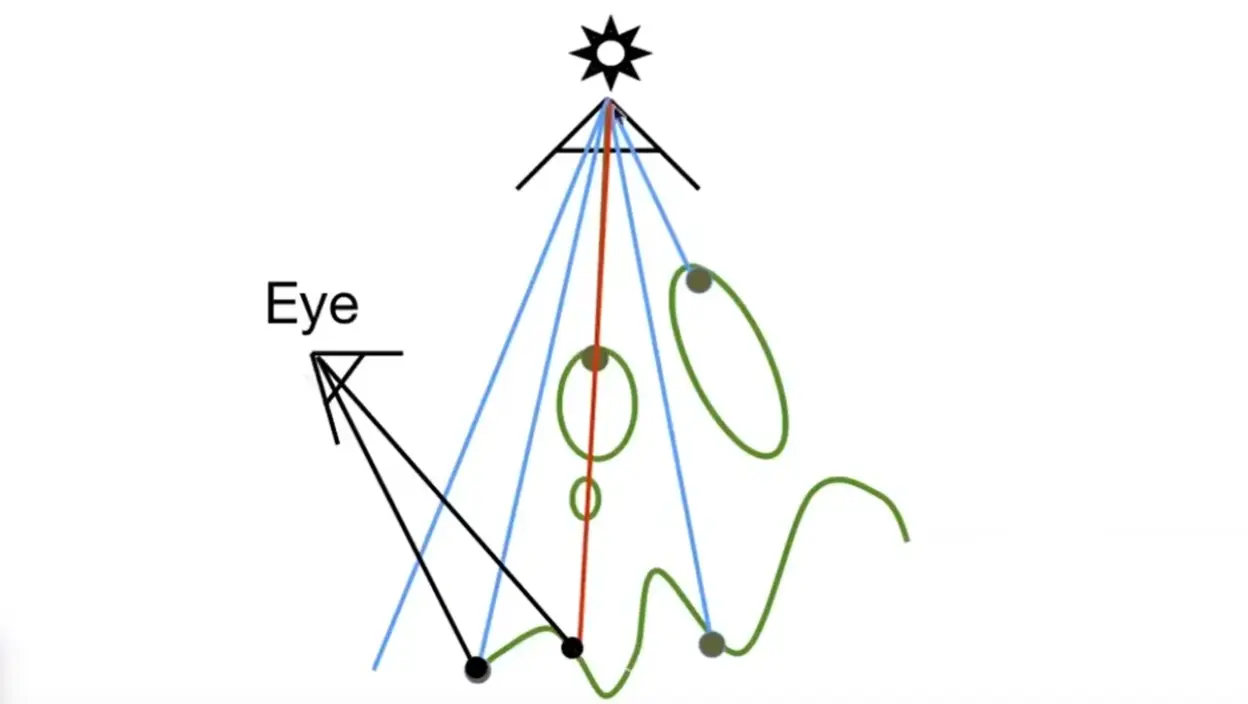
method

1. 光源视角下记录深度图
2. 对于相机看到的一个像素点，映射到光源的深度图上，如果像素到光源的距离和深度图的深度一致，那么被照亮

problems

• 浮点数相等的判断有精度问题，需要允许一个小的 bias，但也不能从根本上解决问题
• 光源深度图的分辨率不能太小，否则会形成锯齿
• 开销很大，需要渲染两遍

Hard Shadow v.s. Soft Shadow

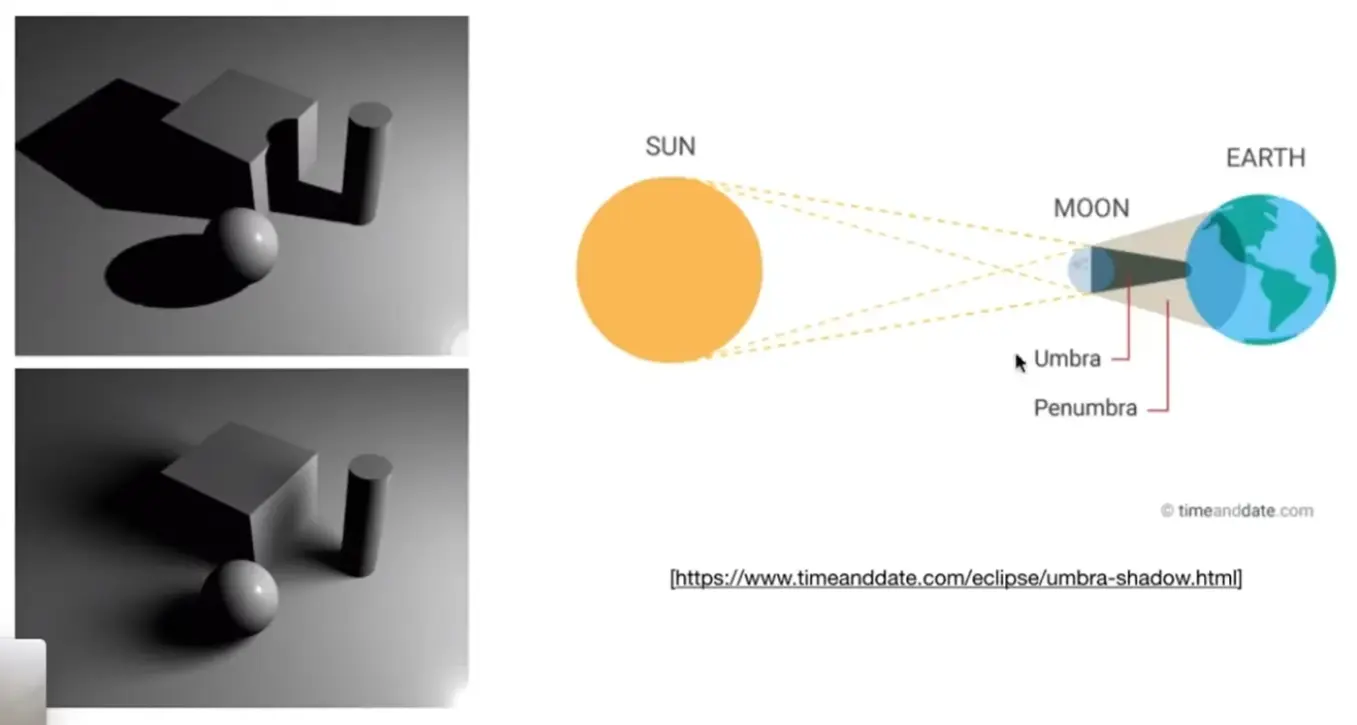
因为光源有一定大小

Comments