Skip to content

Ch.06 Sorting

1 Preliminaries#

void X_Sort ( ElementType A[], int N )

  • N must be a legal integer
  • Assume integer array for the sake of simplicity
  • '>' and '<' operators exist and are the only operations allowed on the input data
  • internal sorting 内部排序

2 Insertion Sort#

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
void InsertionSort( ElementType A[], int N)
{
    int j, P;
    ElementType Tmp;

    for(P = 1; P < N; P++){
        Tmp = A[P];
        for(j = P; j > 0 && A[j-1] > Tmp; j--)
            A[j] = A[j-1];   // move backwards
        A[j] = Tmp;
    }
}
  • worst case, decending sequence, \(T=O(N^2)\)
  • best case, \(T=O(N)\)

3 A Lower Bound for Simple Sorting Algortihms#

  • An Inversion 逆序对，index 大小和值的大小相反，类比逆序数问题，假设逆序数为 n
  • There are \(n\) swaps needed to sort this list by insertion sort
  • \(T(N, I)=O(I+N)\) \(I\)
    • 至少需要数组过一遍 \(N\)
    • 每个逆序对都需要 swap \(I\)
    • 如果本来就接近于排好了，那么接近于 \(O(N)\) Linear
  • The average number of inversion in an random array of N distinct numbers is \(N(N-1)/4\)
  • Any sorting algorithm that sorts by exchanging adjacent elements requires \(\Omega(N^2)\) time on average

3.1 Improvement#

  • 每次排序交换相隔比较远的两个元素

4 Shellsort#

__assets/Ch.06 Sorting/IMG-Ch.06 Sorting-20250125004810877.webp

  • 定义序列 \(h\)，然后进行多次排序，每次 \(h\) 减小，直到最后 \(h=1\)

4.1 Naive Shellsort#

\(h_t=\lfloor N/2\rfloor,\,h_k=\lfloor h_{k+1}/2\rfloor\)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
void Shellsort( ElementType A[], int N )
{
    int i, j, increment;
    ElementType Tmp;
    for(increment = N / 2; increment > 0; increment /= 2)
        /*h sequence*/
        for(i = increment; i < N; i++){
            Tmp = A[i];
            for(j = i; j >= increment; j -= increment)
        }
}

4.1.1 Worst-Case Analysis#

  • \(Theorem\): The worst-case running time of Shellsort is \(\Theta(N^2)\)
  • bad-case可能出现前面 \(h>1\) 排完都不变，最后一次排才排好的情况
  • sequence 选择素数会有更好的效果

4.2 Hibbard's Increment Sequence#

  • \(h_k=2^k-1\)
  • \(Theorem\): The worst-case running time of Shellsort, using Hibbard's increments, is \(\Theta(N^{3/2})\)
  • \(Conjectures\)
    • \(\overline T_{Hibbard}(N)=O(N^{5/4})\)
    • Sedgewick's best sequence is \(\{9*4^i-9*2^i+1\} \cup \{4^i-3*2^i+1\}\)
      • \(T_{avg}(N)=O(N^{7/6})\) \(T_{worst}(N)=O(N^{4/3})\)

5 Heapsort#

  • 如果不需要知道所有的顺序，只需要知道最大/最小的几个值，那么 Heapsort 更快

5.1 Algorithm 1#

1
2
3
4
5
6
7
8
Algorithm1
{
    BuildHeap( H );   /*O(N)*/
    for(i = 0; i < N; i++)
        TmpH[i] = DeleteMin( H );   /*O( log N )*/
    for(i = 0; i < N; i++)
        H[i] = TmpH[i];   /*O(1)*/
}
  • \(T(N)=O(N\log N)\)
  • con: The space requirement is doubled.

5.2 Algorithm 2#

  • 不如直接将 deleteMax 的结果写道数组的后面去
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
void Heapsort( ElementType A[], int N )
{
    int i;
    for(i = N / 2; i >= 0; i--) /*Build Heap*/
        PercDown(A, i, N);
    for(i = N - 1; i > 0; i--){
        Swap(&A[0], &A[i]); /*DeleteMax*/
        PercDown(A, 0, i);
    }
}
  • \(Note\) that A[0] is a valid entry 第零个也是要排序的有效元素
  • 对于任意的数组，平均比较次数 \(2N\log N-O(N\log\log N)\)
  • \(Note\) Although Heapsort gives the best average time, in practice it is slower than a version of Shellsort that uses Sedgewick's increment sequence 因为常数比较大

6 Mergesort#

6.1 Merge two sorted lists#

  • \(T=O(N)\)
  • 两个 pointer，小的放入新数组，并且 ptr 右移一位，直到 ptr 都到达末尾

6.2 Mergesort#

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
void MSort( ElementType A[], ElementType TmpArray[], int Left, int Right )
{
    int Center;
    if(Left < Right){  // if there are elements to e sorted
        Center = (Left + Right) / 2;
        MSort(A, TmpArray, Left, Center);   // T(N/2)
        MSort(A, TmpArray, Center + 1, Right);   // T(N/2)
        Merge(A, TmpArray, Left, Center + 1, Right);   // O(N)
    }
}

void Mergesort( ElementType A[], int N )
{
    ElementType *TmpArray;   // need O(N) extra space
    TmpArray = malloc(N * sizeof(ElementType));
    if(TmpArray != NULL){
        Msort(A, TmpArray, 0, N-1);
        free(TmpArray);
    }
    else FatalError("No space for tmp array!!");
}
  • 为什么要在外部定义 TmpArray
    • 减少内存申请和释放
    • 减少空间开销，递归深度 \(\log N\)，每层都要 \(N\) 长度数组，\(S(N)=O(N\log N)\)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
void Merge( ElementType A[], ElementType TmpArray[], int Lpos, int Rpos, int RightEnd )
{
    int i, LeftEnd, NumElements, TmpPos;
    LeftEnd = Rpos - 1;
    TmpPos = Lpos;
    NumElements = RightEnd - Lpos + 1;
    while(Lpos <= LeftEnd && Rpos <= RightEnd)  // main loop
        if(A[Lpos] <= A[Rpos])
            TmpArray[TmpPos++] = A[Lpos++];
        else
            TmpArray[TmpPos++] = A[Rpos++];
    while(Lpos <= LeftEnd)   // copy rest of first half
        TmpArray[TmpPos++] = A[Lpos++];
    while(Rpos <= RightEnd)   // copy rest of second half
        TmpArray[TmpPos++] = A[Rpos++];
    for(i = 0; i < NumElements; i++, RightEnd--)
        // copy TmpArray back
        A[RightEnd] = TmpArray[RightEnd];
}
\[ \begin{aligned} T(1)&=1\\ T(N)&=2T(N/2)+O(N)\\ &=2^kT(N/2^k)+k*O(N)\\ &=N*T(1)+\log N*O(N)\\ &=O(N+N\log N) \end{aligned} \]
  • pro: 适用于 外部排序
  • cons
    • 需要更多空间 \(S(N)=O(N)\)
    • 数组的复制时很慢的

7 Quicksort#

7.1 The Algorithm#

1
2
3
4
5
6
7
8
void Quicksort ( ElementType A[], int N)
{
    if(N < 2) return;
    pivot = pick any element in A[];
    Partition S = {A[] \ pivot} into two disjoint sets:
        A1 = { a \in S | a <= pivot} and A2 = { a \in S | a >= pivot};
    A = Quicksort(A1, N1) \union { pivot } \union Quicksort(A2, N2);
}
  • Complexity
    • Best case: \(T(N)=O(N\log N)\)
      • 每次 pivot 的选择都是中位数
    • Average case: \(T(N)=O(N\log N)\)
  • Property
    • 每次的 pivot 在后续的排序中位置不会变化，快的原因
    • pivot 选择和 partition 是容易错的地方

7.2 Picking the Pivot#

  • A Wrong Way pivot = A[0]
    • Worst case: if A[] is presorted, \(O(N^2)\)
  • A Safe Maneuver pivot = random select from A[]
    • 随机数产生浪费资源
  • Median-of-Three Partitioning
    • pivot = median(left, center, right) 取其中的中位数

7.3 Partition Strategy#

  • Double Pointer
    • i 和 j，从两边往内走，直到一个
  • 如果 pivot = key
    • i 和 j 都停下来进行 swap
      • 虽然可能存在不必要的交换 \(\{1,1,1,1,1,1,1,1\}\)
      • 但是至少保证了划分的两部分大小相近
        • 否则 \(T(N)=O(N^2)\)

7.4 Small Arrays#

  • Problem: Quicksort is slower than insertion sort for small \(N\le 20\)
  • Solution: N 比较小时，就调用 insertionSort

7.5 Implementation#

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
ElementType Median3( ElementType A[], int left, int right )
{
    int center = (left + right) / 2;
    if(A[left] > A[center]) Swap(&A[left], &A[center]);
    if(A[left] > A[right]) Swap(&A[left], &A[right]);
    if(A[center] > A[right]) Swap(&A[center], &A[right]);
    Swap(&A[center], &A[right-1]); // hide pivot
    return A[right-1];
}

void Qsort( ElementType A[], int left, int right )
{
    int i, j;
    ElementType pivot;
    if(left + CUTOFF <= right){
        pivot = Median3(A, left, right); // select pivot
        i = left; j = right - 1;
        for(;;){
            while(A[++i] < pivot);
            while(A[--j] > pivot); // stop at invalid element
            if(i < j) Swap(&A[i], &A[j]); // adjust partition
            else break; // partion done
        }
        Swap(&A[i], &A[right - 1]); // restore pivot
        Qsort(A, left, i-1);
        Qsort(A, i+1, right);
    }else InsertionSort(A + left, right - left + 1)
}

void Quicksort( ElementType A[], int N )
{
    Qsort(A, 0, N-1);
}
  • Note: Median3 调用后，左中右的三个元素已经排好了，但是由于 ++i --j，实际上跳过了这来哥哥元素。

7.6 Analysis#

  • \(T(N) = T(i)+T(N-i-1)+cN\)
  • Worst case: \(T(N)=T(N-1)+cN=O(N^2)\)
  • Best case: \(T(N)=2T(N/2)+cN=O(N\log N)\)
  • Average case
    • Assume the average value of \(T(i)\) for any \(i\) is \(\frac{1}{N}[\sum_{j=0}^{N-1}T(j)]\)
    • \[T(N)=\frac{2}{N}[\sum_{j=0}^{N-1}T(j)]+cN=O(N\log N)\]

Quicksort to find the kth largest element

每次找到 pivot 进行 partition 之后，计算大的一边的元素个数，判断第 k 大的元素在哪边，直到其出现在 pivot
\(T(N)=O(N)\) Linear

  • Space Complexity 等于递归深度 \(O(\log N)\)
    • 最坏情况 \(O(N)\)

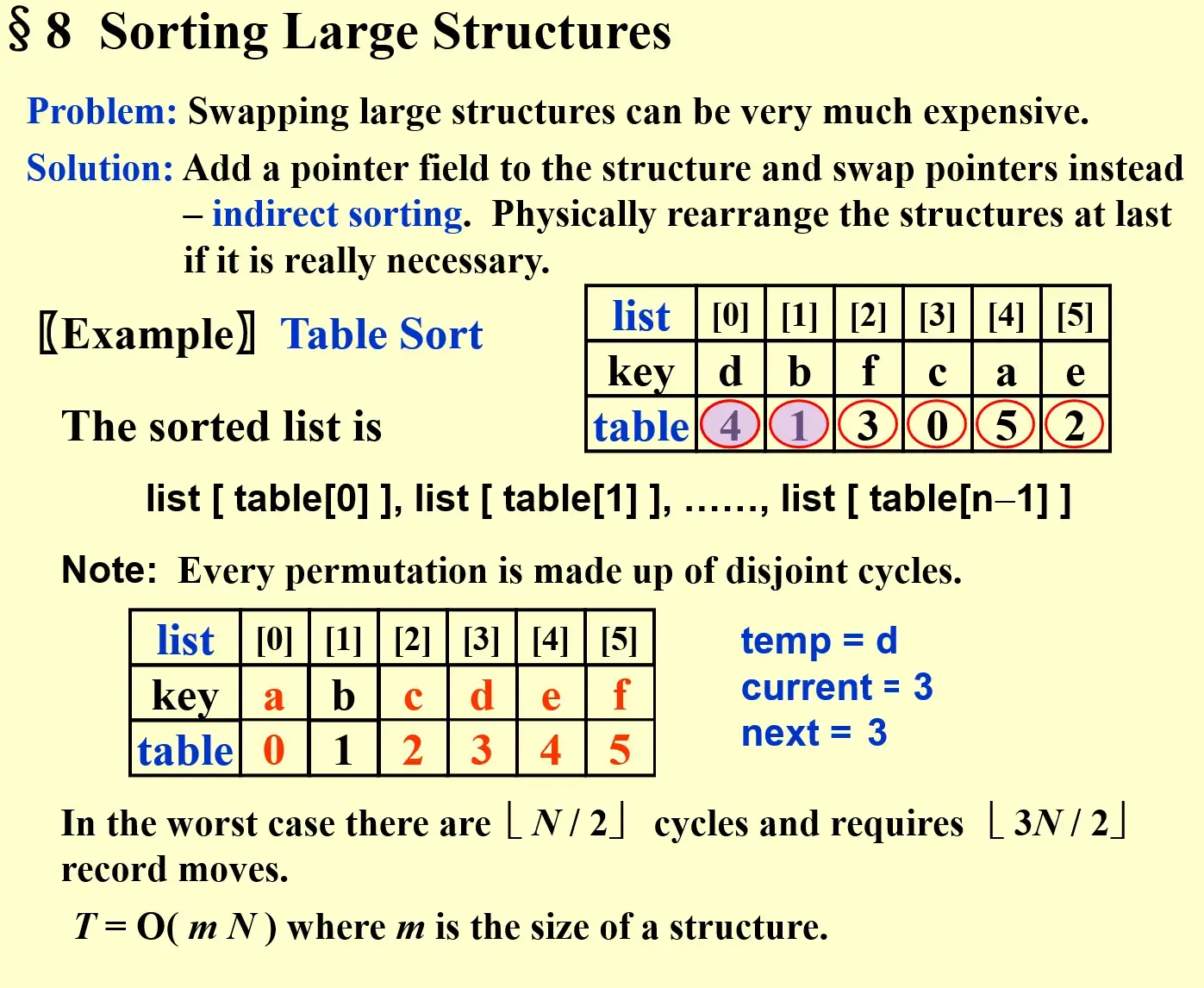
8 Sorting Large Structures#

  • Solution: Add a pointer field to the structure and swap ptrs instead
  • Table Sort
    • 对于所有的 key，先创建一个 table[]，用来存储目标的 index
      • 构成了 cycle，也就是通过 list index 和 table 目标位置构成的需要交换的 cycle!__assets/Ch.06 Sorting/IMG-Ch.06 Sorting-20250125004937209.webp
      • 具体操作时
        • 先进行 tablesort
          • table 初始化为 [0, 1, 2, 3, 4, 5]
          • 依据 key 对 table 中的 index 进行排序
        • 然后交换 key
          • 遍历 list，只要出现了 list index != table element，那么就进行 cycle exchange
            • 记录这个 entry 以及这个 key
            • 进行轮换，直到遇到一个元素的 table element == entry 结束
    • Note: Every permutation is made up of disjoint cycles
  • Analysis
    • worst case, \(\lfloor N/2\rfloor\) cycles and \(\lfloor 3N/2\rfloor\) record moves
    • \(T=O(mN)\) where \(m\) is the size of the structure

9 A General Lower Bound for Sorting#

  • \(Theorem\) Any algorithm that sorts by comparisons only must have a worst case computing time of \(\Omega(N\log N)\)
    • Can be proved by decision tree
    • __assets/Ch.06 Sorting/IMG-Ch.06 Sorting-20250125004959687.webp

10 Bucket Sort and Radix Sort#

10.1 Bucket Sort#

  • 对于离散、取值范围很小的数据
  • 创建所有数据取值点的 bucket，每个称为 slot槽
  • 线性遍历数组，是哪个就放在哪个 slot
  • \(T(N, M) = O(M+N)\)
    • 如果 \(M\) 远大于 \(N\)，那么效率会很低，不如 quicksort

10.2 Radix Sort#

__assets/Ch.06 Sorting/IMG-Ch.06 Sorting-20250125005012173.webp

  • 进行多轮排序，每次排一个数位，Least Significant Digit First
  • \(T=O(P(N+B))\)
    • \(P\) 是 number of passes，也就是位数
    • \(B\) 是 number of buckets

10.2.1 MSD (Most Significant Digit)#

  • 高位分到 bucket 之后，每个 bucket 内部
    • 可以使用任意的排序算法
    • 可以并行操作

10.2.2 LSD (Least Significant Digit)#

  • 高位的排序依赖于低位的排序
  • 只能串行进行

11 HW#

  • After the first run of Insertion Sort, it is possible that no element is placed in its final position
    • T
  • Shell sort is stable.
    • F
    • stable 指的是相同的元素在排序前后的顺序是不变的
      • 假设存在两个相等的元素，排序之后原本在前面的还是在前面
  • Mergesort is stable. T
  • During the sorting, processing every element which is not yet at its final position is called a "run". Which of the following cannot be the result after the second run of quicksort?
    • __assets/Ch.06 Sorting/IMG-Ch.06 Sorting-20250125005025810.webp
    • 注意
      • 这里 quicksort 的 run 指的是递归深度，两层递归能够选定 3 个 pivot 位置
      • 这里的 quicksort 实现方式不是选中位数
    • A 可能是 72 28
    • B 可能是 2 72
    • C 可能是 2 28
    • D 不可能，只有 32

Comments