Ch.03 List

1 Abstract Data Type (ADT)

• \(Data Type = \{Objects\} \cup \{Operations\}\)
• ADT: The specification on objects and specification of the operations on the objects are separated from the representation of the objects and implementation on the operations.
  • 封装，函数化编程，不考虑具体实现

2 The List ADT

2.1 Operations

• FindLength
• PrintList
• MakeEmpty
• FindKthElement
• InsertAfterKth
• Delete
• FindNext
• FindPrevious

2.2 Implementation

• Array
  • 需要提前估计容量
  • 插入删除 O(N)，移动数据
  • 查找 k-th O(1)

2.2.1 Linked List

• 使用 dummy head node，可以删除第一个

2.2.2 Doubly Linked Circular Lists

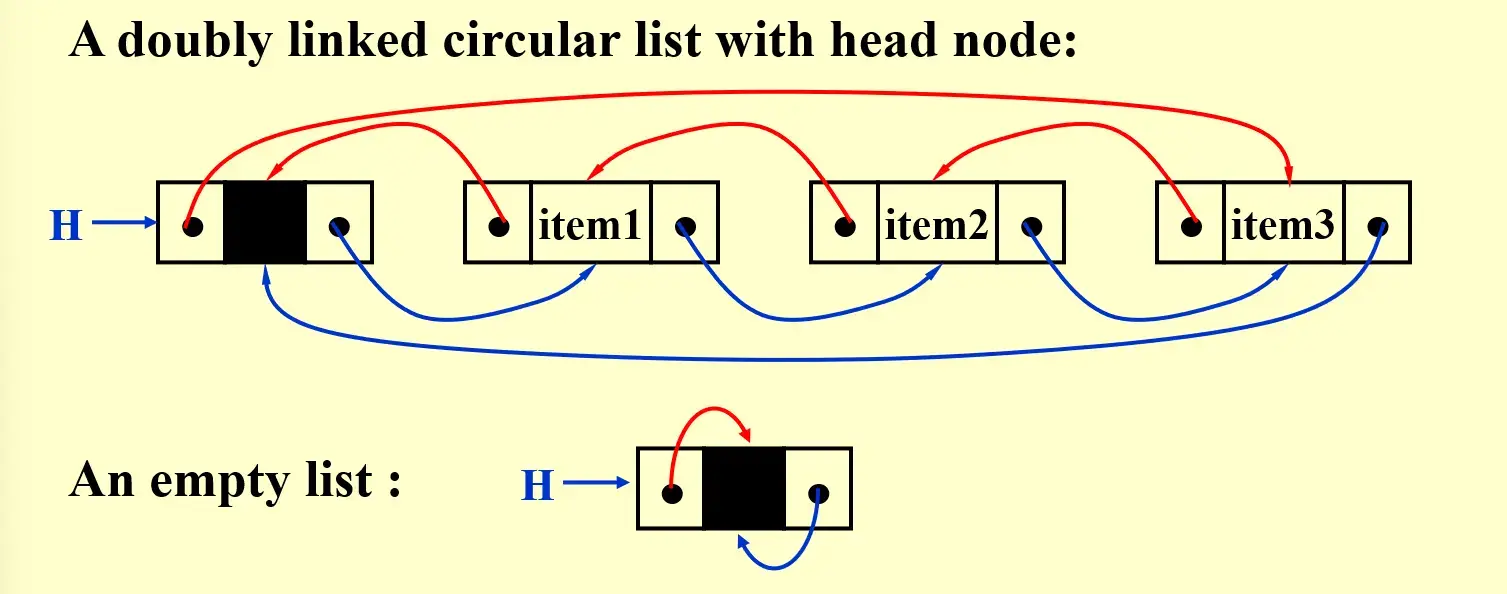
• 方便查找 previous

2.3 Two Applications

2.3.1 The Polynomial ADT 多项式表示

• coefficient 系数 exponent 指数
• Operations
  • FindDegree 找到最高次项指数
  • Addition
  • Subtration
  • Multiplication
  • Differentiation

2.3.1.1 Representation 1

typedef struct {
    int CoeffArray [MaxDegree + 1];
    int HighPower;
} *Polynomial

• 对于稀疏数组，过于复杂

2.3.1.2 Representation 2

typedef struct poly_node *poly_ptr;
struct poly_node {
    int Coefficient;
    int Exponent;
    poly_ptr Next;
} ;
typedef poly_ptr a; // nodes sorted by exponent

2.3.2 Multilists

Ch.09 Graph Algorithms#1.1.3 Adjacency Multilists 也使用到了 multilist 的思想

For example, represent the relationship between students and the courses. Array would be too complex in space

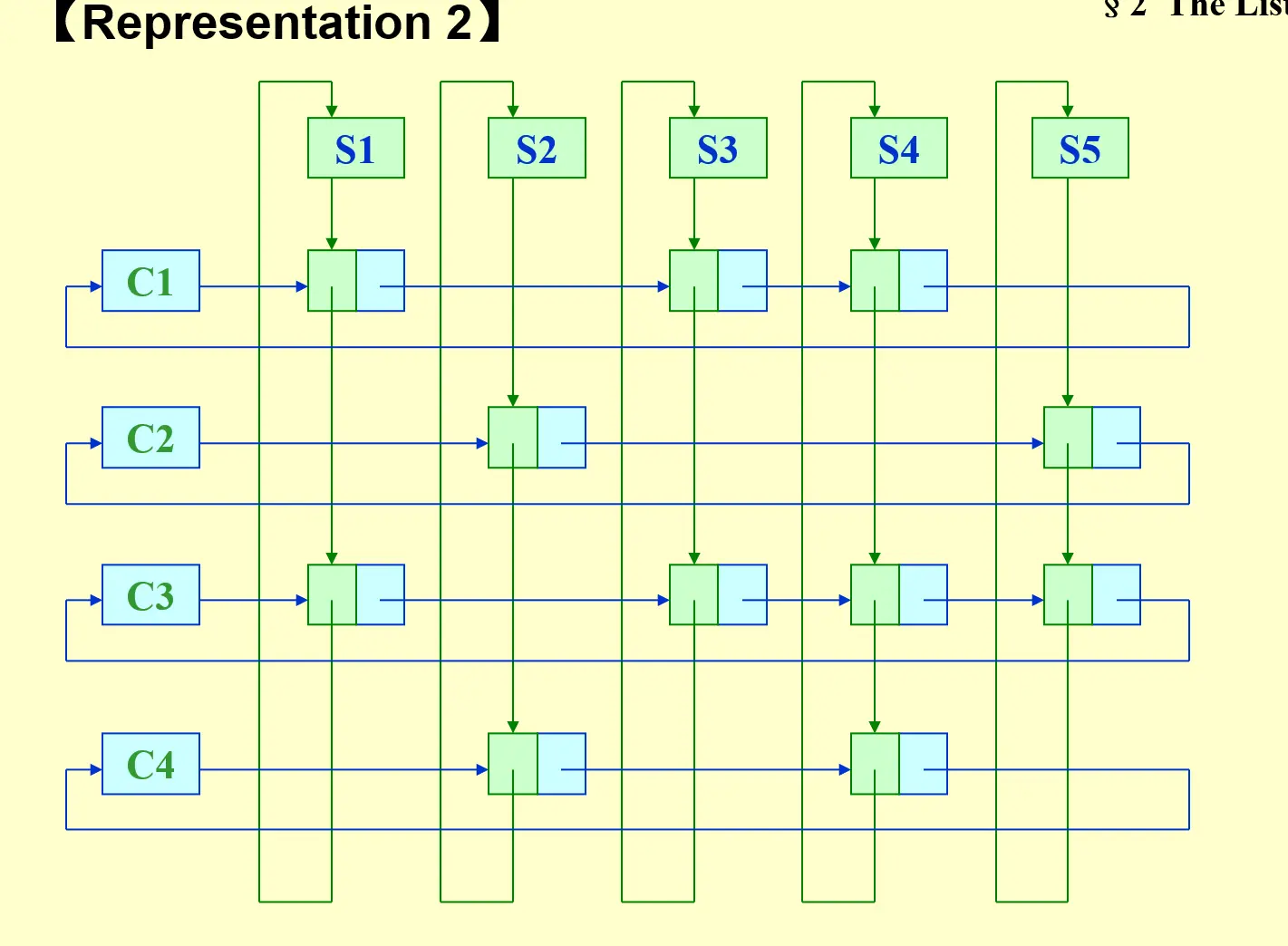
• 每个节点表示一个 pair relationship，节点内要存储学生编号和课程编号

HW: Sparse matrix representation

1. 坐标列表（Coordinate List, COO）： 在这种表示中，矩阵被表示为三个数组：行索引、列索引和数据值。每个非零元素由其行索引、列索引和值组成。

2. 压缩稀疏行（Compressed Sparse Row, CSR）： CSR 表示由三个数组组成：非零元素的值、行指针和列索引。行指针数组指向列索引数组中每个行的起始位置。这种表示方式适合于行操作，如行的插入和删除。

3. 压缩稀疏列（Compressed Sparse Column, CSC）： CSC 与 CSR 类似，但是是按照列来组织的。它包含三个数组：非零元素的值、列指针和行索引。列指针数组指向行索引数组中每个列的起始位置。这种表示方式适合于列操作。

4. 字典式（Dictionary of Keys, DICTIONARY）： 这种表示方法使用字典（或哈希表）来存储非零元素的位置和值，键是元素的索引对（行索引，列索引）。

5. 块稀疏矩阵（Block Sparse Matrix）： 当矩阵的稀疏性在子矩阵级别上时，可以使用块稀疏矩阵表示。这种表示将矩阵分割成小块，并且只存储那些非零的块。

6. 带状稀疏矩阵（Banded Sparse Matrix）： 当非零元素仅出现在矩阵的主对角线附近的几条对角线上时，可以使用带状稀疏矩阵表示。这种表示通常包含对角线宽度和非零元素。

2.3.3 Cursor Implementation of Linked Lists (no pointer)

• 维护一个 freelist ，等价为从 0 开始的循环链表
• malloc，就是在 freelist 中删去 0 之后的节点
• free，就是将一个节点添加到 freelist 0 之后

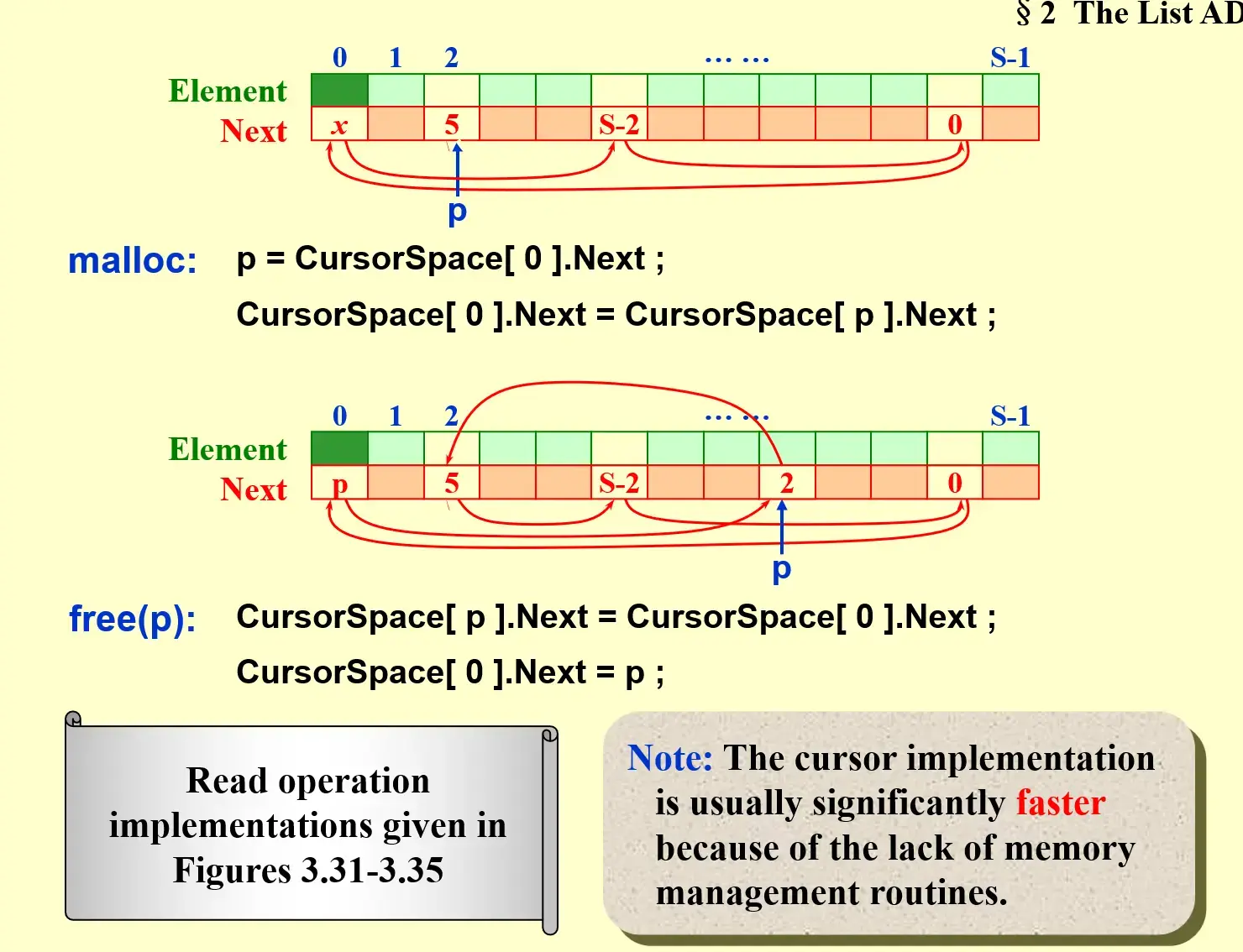
Title

• malloc 可以看出 CursorSpace[0].Next 总是队尾的空位，且队尾的下一个一定是空的
• free 操作的原理
  • 将原本队尾第一个空位放在要删除的元素后面
  • 将 CursorSpace[0].Next 指向要删除的元素

3 The Stack ADT

3.1 Operations

int IsEmpty( Stack S );
Stack CreateStack();
DisposeStack( Stack S );
MakeEmpty( Stack S );
Push( ElementType X, Stack S );
ElementType Top( Stack S );
void Pop( Stack S );

• 满的 stack push error
• 空的 stack pop error

3.2 实现方法

3.2.1 链表实现

• dummy head 指向栈顶元素，相当于链表插入头节点
• 出栈需要 free() ，但是可以使用一个 recycle bin 链表来存储所有 pop 出来的元素，减少 free 的次数有利于提升性能

3.2.2 数组实现

typedef struct {
    int StackSize;
    int Top;    // top pointer
    Element type *Array;
} Stack;

• 一定要封装好，不能让主程序能够直接读取非栈顶元素
• 对于 pop, push 需要进行检查

3.3 Application

3.3.1 Balancing Symbols

• 检查字符串中的括号等是否能过够配对
• On-line \(T(N)=O(N)\)

3.3.2 Postfix Evaluation

3.3.2.1 逆波兰表达式

• a+b*c-d/e infix expression 中缀表达式
• - + a * b c / d e prefix expression 前缀表达式
• a b c * + d e / - postfix evalution 逆波兰表达式

3.3.2.2 操作方法

• 遇到元素，入栈
• 遇到符号，把栈顶两个元素拿出来处理，结果再入栈
• 算完之后输出栈内唯一元素

3.3.3 Infix to Postfix Conversion

3.3.3.1 没有括号的话

• 读到元素直接输出
• 读到符号
  • 如果栈顶符号优先级 \(\ge\) 当前读到的符号，出栈
  • 否则，入栈
• 最后 pop 剩余的符号

3.3.3.2 有括号

a*(b+c)-d ->

• 读到元素直接输出
• 读到符号（包括括号）
  • if 读到 (，入栈
  • else if 读到 )，一直出栈到左括号
  • else if 栈顶不是 ( && 栈顶符号优先级 \(\ge\) 当前读到的符号，出栈
  • else 入栈

可以理解为

• 读到 ( 一定入栈
• 读到 ) 才能让 ( 出栈，而且中间的全部出栈
• 其他一样

注意，这个问题需要单独分析

Note:  a – b – c will be converted to a b – c –.  However, 2^2^3 ( \(2^{2^3}\) ) must be converted to 2 2 3 ^ ^, not 2 2 ^ 3 ^ since exponentiation associates right to left.

3.3.4 Function Calls - System Stack

• 系统里有两个指针，分别是 sp, stack pointer fp, frame pointer
• 尾递归可以优化成循环，编译器可以实现这种优化
• 递归会消耗大量系统资源，效率很低
  • 能用递归完成的操作都一定可以不用递归完成

4 The Queue ADT

• 与栈相反，first in first out
• 尾部插入，队首取出

int IsEmpty( Queue Q );
Queue CreateQueue();
void DisposeQueue( Queue Q );
void MakeEmpty( Queue Q );
void Enqueue ( ElementType X, Queue Q );
ElementType Front( Queue Q );       // 获取队列第一个元素
void Dequeue( Queue Q );

4.1 实现

4.1.1 Array Implementation

struct QueueRecord {
    int Capacity;
    int Front;
    int Rear;  //Rear == -1 队列为空
    int Size;   // current size
    ElementType *Array;
}

4.1.2 Circular Queue

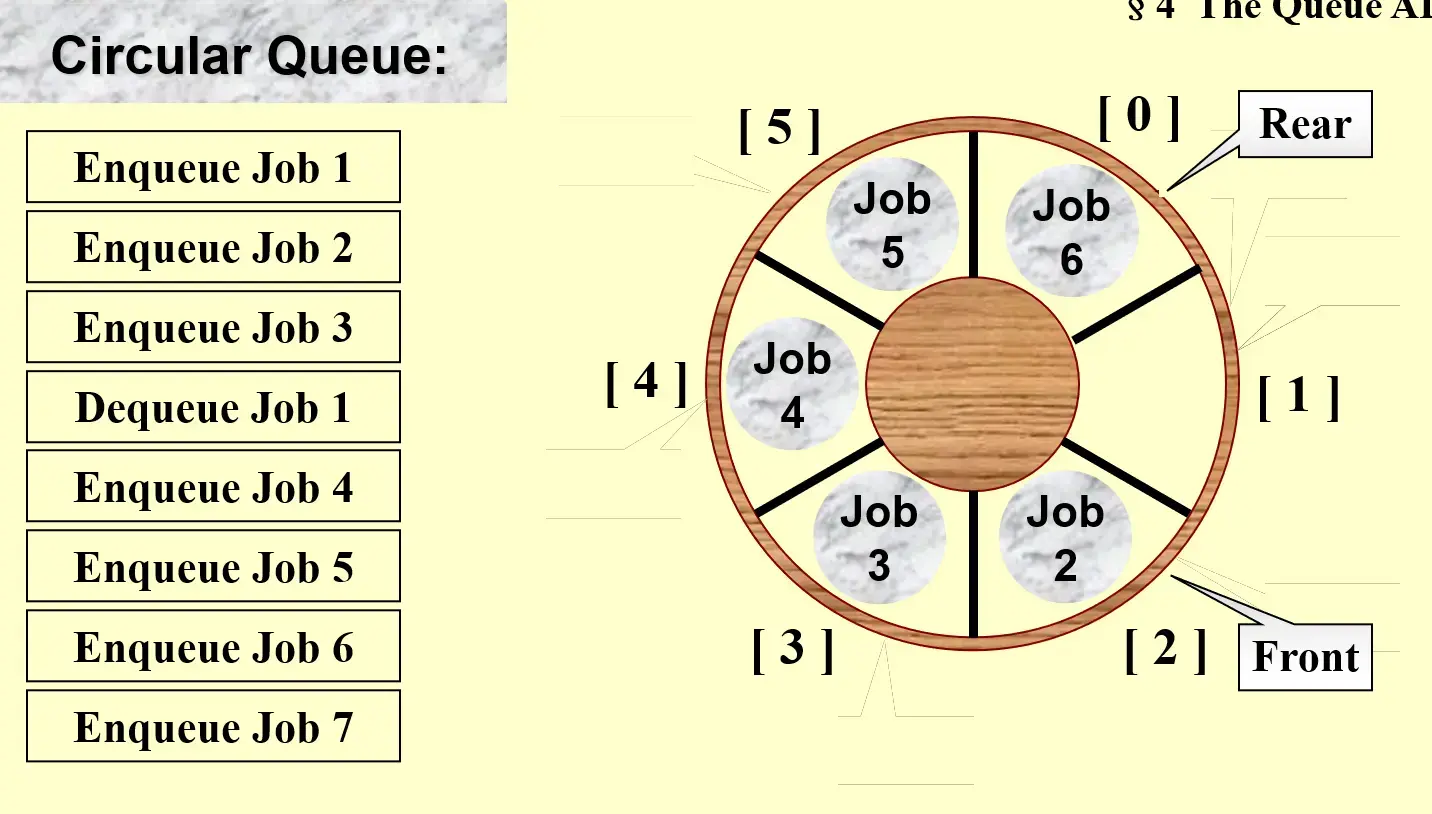
• 队列首尾相接，相当于数组最后添加元素添加到数组的开头
• Rear 默认在 0，Front 默认在 1
  • Enqueue 时，rear++ 在 rear 加入 job
  • Dequeue 时，删去 front 的 job，front++
  • Rear 和 Front 差 2 认为是满栈，差 1 认为是空栈

5 HW

• Sequential List 就是顺序表，就是数组
• 
  • 由于 ps 不能变位置，只有前面的三个 o 可以以任意顺序输出
  • 这样找到所有的可能
    • i i i o o o
    • i i o ...
      • i i o i o o
      • i i o o i o
    • i o i ...
      • i o i i o o
      • i o i o i o
    • i o o 不允许，已经空
• 
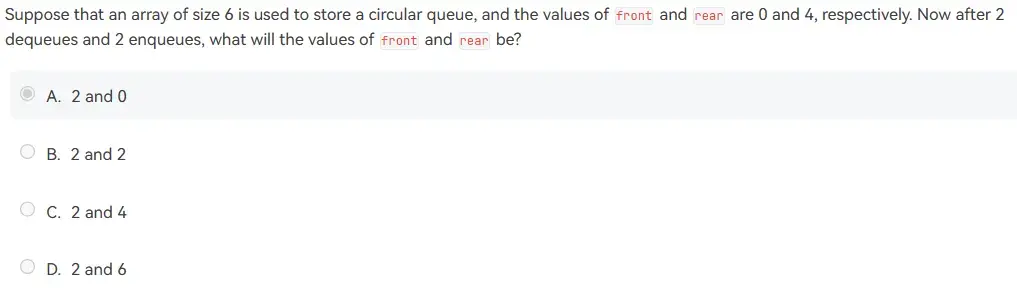
  • 结合 4.1.2 Circular Queue 内容思考

Comments