Ch.04 Trees

1 Preliminaries#

1.1 Definition#

A tree is a collection of nodes. The collection can be empty, which is sometimes denoted as A. Otherwise, a tree consists of a distinguished node r, called the root, and zero or more (sub)trees T 1, T 2, . . . , Tk, each of whose roots are connected by a directed edge to r.
- 这是一个递归的定义
Note
- subtrees must not connect to each other
- there are N-1 edges in a tree with N nodes
Degree
- for a node, degree(node) = the number of its children node
- for a tree, it is the maximum of degree of its node
Parent, children, sibilings, leaf 都是特殊定义的节点
Path: the path from node A to node B is unique in a tree 只能是从上到下走
- Length of path: 路径中边的个数
Depth: the length of the path from root to this node, Depth(root)=0
Height the length of the longest path from this node to a leaf, height(leaf)=0
height(depth) of a tree = height(root) = depth(deepest leaf)
Ancestors: all the nodes along the path from this node up to the root
descendants: all the nodes in its subtrees

1.2 Implementation#

1.2.1 List Representation#

可以用 (A(B(E,F),C,D)) 的线性结构来表示
可以用链表来表示
- 劣势：tree 在生长的时候每个节点需要几个 pointer 不好确定
  - 如果提前知道了 degree，也会浪费空间

1.2.2 FirstChild-NextSibiling Representation#

每个 node 都有两个 pointer，第一个指向 firstchild，第二个指向 nextsibiling
表达不唯一，子节点的顺序是不重要的

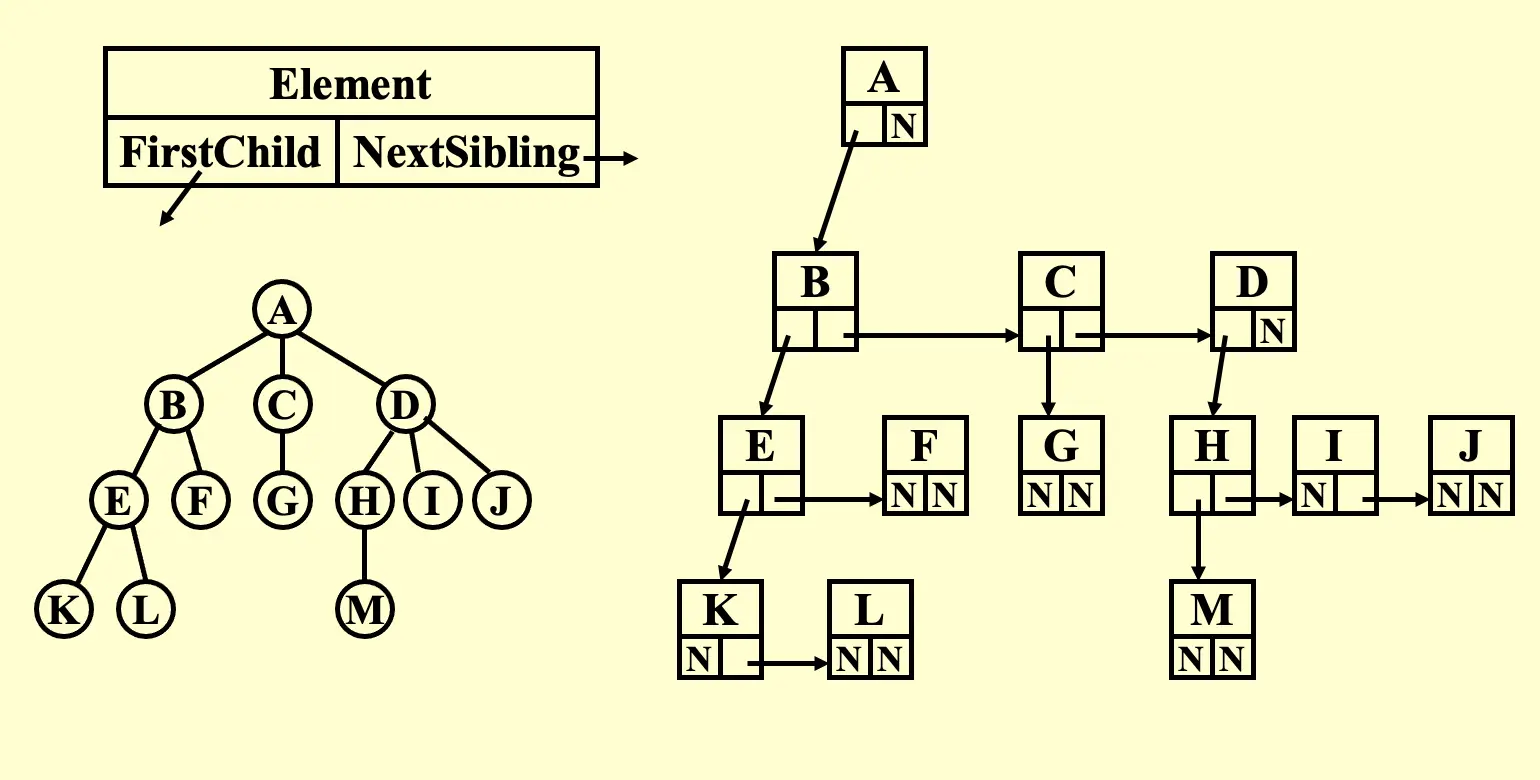
__assets/Ch.04 Trees/IMG-Ch.04 Trees-20250125004334370.webp

general tree can be converted into a Binary Tree

2 Binary Tree#

2.1 Definition#

每个节点最多只能有两个子节点
相当于 general 的 firstchild-nextsibiling 表达旋转 45°

2.2 Applications#

2.2.1 Expression Tree (syntax trees)#

review: postfix expression -> stack
constructing an Expression Tree from postfil expression
- operand, push
- operatior, operator 指向栈顶两个元素，push operator 的指针

2.3 Tree Traversels#

preorder 先根遍历，根左右
postorder 后根遍历，左右根
levelorder 深度遍历
- 使用 queue 存储将要遍历的节点指针
- 每遍历一个节点，将它的子节点加入队列
Inorder Traversal 中根遍历，左根右
- 先左子树，再根节点，再右子树
- 递推形式非常复杂，递归很好读

void iter_inorder( tree_ptr tree )
{
    Stack S = CreateStack(MAX_SIZE);
    for(;;) {
        for(; tree; tree = tree->left) Push(tree, S);
        tree = Top(S); Pop(S);
        if(!tree) break;
        visit(tree->Element);
        tree = tree->Right;
    }
}

2.3.1 expression tree#

按照不同的遍历方式，能得到不同的表达式，这就是 expression tree 的作用
perorder: prefix exp
inorder: infix exp
postorder: postfix exp

2.3.2 print directory#

使用 preorder 遍历，先打印根目录
记录 depth，用作 print 的缩进

2.3.3 Calculating the size of a directory#

使用 postorder，先计算子节点（文件或文件夹）的大小，在返回子节点
\(T(N)=O(N)\)

2.4 Different Binary Trees#

2.4.1 Threaded Binary Trees 线索二叉树#

一个二叉树有 n 个节点，那么它就一定有 n+1 个空的指针，所以为了避免浪费可以使用 threads
Rules: 有一个 dummy head node
1. 如果左指针空，替换为中序遍历的前驱
  1. 如果没有前驱，替换为 dummy head node
2. 如果右指针空，替换为中序遍历的后继
便于从下面来往上遍历

2.4.2 Other binary trees#

Skewed Binary Trees: 斜树，退化成线性结构 表达能力很弱，不如用 linear list
Complete Binary Trees: 完全二叉树 ^bfe95b
- 除了最后一层，全都填满
- 最后一层从左往右填

2.5 Properties of Binary Trees#

第 i 层最大有 \(2^{i-1}\) 个节点
k 层二叉树的最大节点个数为 \(2^k-1\)
完全二叉树中，叶子节点的个数比 2 度节点个数多 1 \(n_0=n_2+1\)
- 或者这样理解
  - 如果没有二度节点，只会有一个叶子
  - 每多一个二度节点，就能多一条支路，多一个叶子

3 The Search Tree ADT - Binary Search Tree#

3.1 Definition#

每个节点都有一个 key，为整数，每个 key 不同
左子树的 key 都小于 root
右子树的 key 都大于 root
Binary Search Tree 的子树也是 Binary Search Tree

3.2 ADT#

Objects: A finite ordered list with zero or more elements
Operations

SearchTree MakeEmpty( SearchTree T );
Position Find( ElementType X, SearchTree T );
Position FindMin( SearchTree T );
Position FindMax( SearchTree T );
SearchTree Insert( ElementType X, SearchTree T );
SearchTree Delete( ElementType X, SearchTree T );
ElementType Retrieve( Position P );

3.3 Implementations#

3.3.1 Find#

递归可以实现
由于是尾递归，可以优化为循环
时间复杂度，就是树的深度 d

Position Iter_Find( ElementType X, SearchTree T )
{
    while(T){
        if(X == T->Element) return T;    // found
        else if(X < T->Element) T = T->Left;
        else T = T->Right;
    }
    return NULL;    // not found
}

3.3.2 FindMin/FindMax#

找到左下角/右下角的节点 循环解决
时间复杂度为 d

3.3.3 Insert#

找到待插入的位置（父节点）
- 进行和 Find 一样的操作
- 最后一个遇到的节点就是这个数的父节点
创建节点并返回指针
上一层调用中使父节点的指针等于这个新节点的指针
\(T(N)=O(d)\)

SearchTree Insert( ElementType X, SearchTree T )
{
    if(T == NULL){ // the initial T is NULL, or the position of X is found
        T = (SearchTree)malloc(sizeof(struct TreeNode));
        if(T == NULL) FatalError("Out of space!!");
        else{
            T->Element = X;
            T->Left = NULL; T->Right = NULL;
        }
    }
    else{
        if(X < T->Element) T->Left = Insert(X, T->Left); // need to update T->Left in this recursion
        else if(X > T->Element) T->Right = Insert(X, T->Right);
        // else X already exist, do nothing
    }
    return T;   // make this return because the original T is allowed to be NULL, thus we need to build such a tree and ptr to it!!!
}

3.3.4 Delete#

delete leaf node: free 并将父节点指向空
delete 1 degree node: 将它的子节点直接接到父节点上
delete 2 degree node:
- 将这个节点替换为左子树中最大的，或右子树中最小的
- 对被换过来的这个节点递归进行 delete 操作

SearchTree Delete( ElementType X, SearchTree T )
{
    Position TmpCell;
    if(T == NULL) Error("Element not found");
    if(X < T->Element) T->Left = Delete(X, T->Left);    // go left
    else if(X > T->Element) T->Right = Delete(X, T->Right); // go right
    else{   // found, just this node
        if(T->Left && T->Right){    // two child
            TmpCell = FindMax(T->Left);
            T->Element = TmpCell->Element;
            T->Left = Delete(T->Element, T->Left);
        }
        else{       // one or no child
            TmpCell = T;
            if(T->Left) T = T->Left;    // left not empty, replace with left
            else if(T->Right) T = T->Right; // right not empty, replace with right
            free(TmpCell);  // don't forget to free memory!
        }
    }
    return T;   // if deleted, ptr has to be updated
}

3.3.4.1 Lazy Deletion#

使用一个 flag 来标记这个节点是否 active，标记为 deleted 就可以，用于减少 free 操作
如果二叉树比较平衡的话，使用 lazy deletion 只会使搜索的时间复杂度增加一点点

3.4 Average-Case Analysis#

建立一个 n 个节点的 binary search tree
\(height(bst)\in[h-1,\lceil\log_2(n+1)\rceil-1]\)

4 HW 4#

There exists a binary tree with 2016 nodes in total, and with 16 nodes having only one child. F
1. 去除所有的单个孩子的节点，剩下 2000 个节点的完全二叉树，但 2000 不是 2 的次方数
Given a tree of degree 3. Suppose that there are 3 nodes of degree 2 and 2 nodes of degree 3. Then the number of leaf nodes must be ____.
1. 如果所有的 degree 都是 1，那么只有一个叶子节点
2. every extra degree add 1 leaf node
3. 1+3+2*2=8
If a general tree T is converted into a binary tree BT, then which of the following BT traversals gives the same sequence as that of the post-order traversal of T?
1. left right root
2. the sequence of M H I J D
3. T preorder = BT preorder; T postorder = BT inorder
Among the following threaded binary trees (the threads are represented by dotted curves), which one is the postorder threaded tree?
1. threaded binary tree 空指针的替换规则可以是 postorder, inorder, preorder

4.1 函数题：Isomorphic 同构树#

4.1.1 Idea 1#

需要使用递归，每次判断一层，然后拆成子树再次判断
degree 不相等直接返回 0
- 对于 degree = 2 节点在本层，判断下一层的 value 是否对应
  - 对应，则对应递归调用
  - 不对应，则返回 0
- 对于 degree = 1 节点在本层，判断下一层的 value 是否对应
- 对于 degree = 0 的节点返回 1

4.1.2 Idea 2#

判断值是否相等，不相等返回 0
判断 degree
- not equal return 0
- = 2
  - if tree 1 left == tree 2 left
    - iso(left, left)
    - iso(right, right)
  - else
    - iso(left, right)
    - iso(right, left)
- =1
  - 相应调用

4.1.3 易错点、改进建议#

需要考虑对两个空树调用的情况
使用 bitmap 来统一表示，可以稍微减少判断的问题

4.2 编程题：ZigZagging on a Tree#

4.2.1 Question#

how to build a tree from inorder array and postorder array?
how to traversal this binary tree in required form?
build binary tree
traversal it

4.2.2 idea 1: abandoned 空间太大了，其实操作很简单，真正建立树的结构没有用#

4.2.2.1 建立树#

拿到 postorder 的最后一个元素作为 pivot
在 parent 下建立这个节点
在 inorder 中找到这个 pivot，查询左右子树长度
递归调用，分别传入 root 的左右指针
当 size = 1 时，建立这个节点，递归出口

4.2.2.2 遍历树#

4.2.3 idea 2#

使用一个二维数组 inorder 标记每个数字的深度？
- 需要用到遍历，每次取 postorder 的最后一个数字为 pivot，设置这个 pivot 的深度，并递归求子树元素的深度
然后直接交叉遍历数组？

4.2.3.1 评价：非常好，一遍过！很省空间#

最后换成单独的 depths 数组，维护起来比较方便

4.2.3.2 建议#

注意输出格式的限制，末尾是否允许有多余的空格
注意这是 C 语言，不是 python
三目运算符 int max = a>b?a:b;

5 HW#

There exists a binary tree with 2016 nodes in total, and with 16 nodes having only one child. F
- 根据 2.5 Properties of Binary Trees 进行推导得出 \(2n_2=1999\) 除不尽，所以不可能
In a binary search tree which contains several integer keys including 4, 5, and 6, if 4 and 6 are on the same level, then 5 must be their parent. F
- False: 可以是三层的树，5 为根，4 为右孩子，6 为左孩子
- 下列二叉树中，可能成为折半查找判定树（不含外部结点）的是（）_下列二叉树中,可能成为折半查找判定树(不含外部结点)的是:-CSDN博客

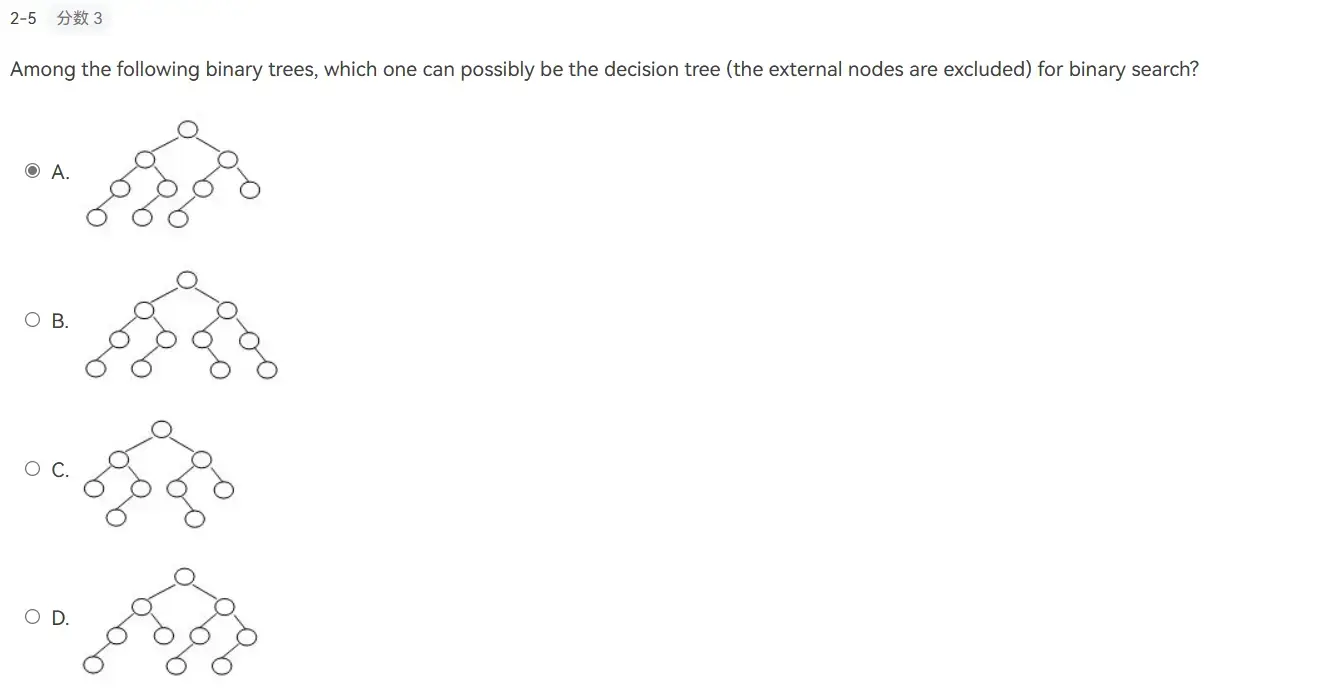
6 Review#

The time comlexity of Binary Search will be the same no matter we store the elements in an array or a linked list.
- F, idkw

Ch.04 Trees

1 Preliminaries#

1.1 Definition#

1.2 Implementation#

1.2.1 List Representation#

1.2.2 FirstChild-NextSibiling Representation#

2 Binary Tree#

2.1 Definition#

2.2 Applications#

2.2.1 Expression Tree (syntax trees)#

2.3 Tree Traversels#

2.3.1 expression tree#

2.3.2 print directory#

2.3.3 Calculating the size of a directory#

2.4 Different Binary Trees#

2.4.1 Threaded Binary Trees 线索二叉树#

2.4.2 Other binary trees#

2.5 Properties of Binary Trees#

3 The Search Tree ADT - Binary Search Tree#

3.1 Definition#

3.2 ADT#

3.3 Implementations#

3.3.1 Find#

3.3.2 FindMin/FindMax#

3.3.3 Insert#

3.3.4 Delete#

3.3.4.1 Lazy Deletion#

3.4 Average-Case Analysis#

4 HW 4#

4.1 函数题：Isomorphic 同构树#

4.1.1 Idea 1#

4.1.2 Idea 2#

4.1.3 易错点、改进建议#

4.2 编程题：ZigZagging on a Tree#

4.2.1 Question#

4.2.2 idea 1: abandoned 空间太大了，其实操作很简单，真正建立树的结构没有用#

4.2.2.1 建立树#

4.2.2.2 遍历树#

4.2.3 idea 2#

4.2.3.1 评价：非常好，一遍过！很省空间#

4.2.3.2 建议#

5 HW#

6 Review#

Comments