05 Collision Detection

Intro

• = physics simulation
• Naive method
  • 直接判断两个像素结合是否有交集
  • low efficiency

Rect Collision Algorithm

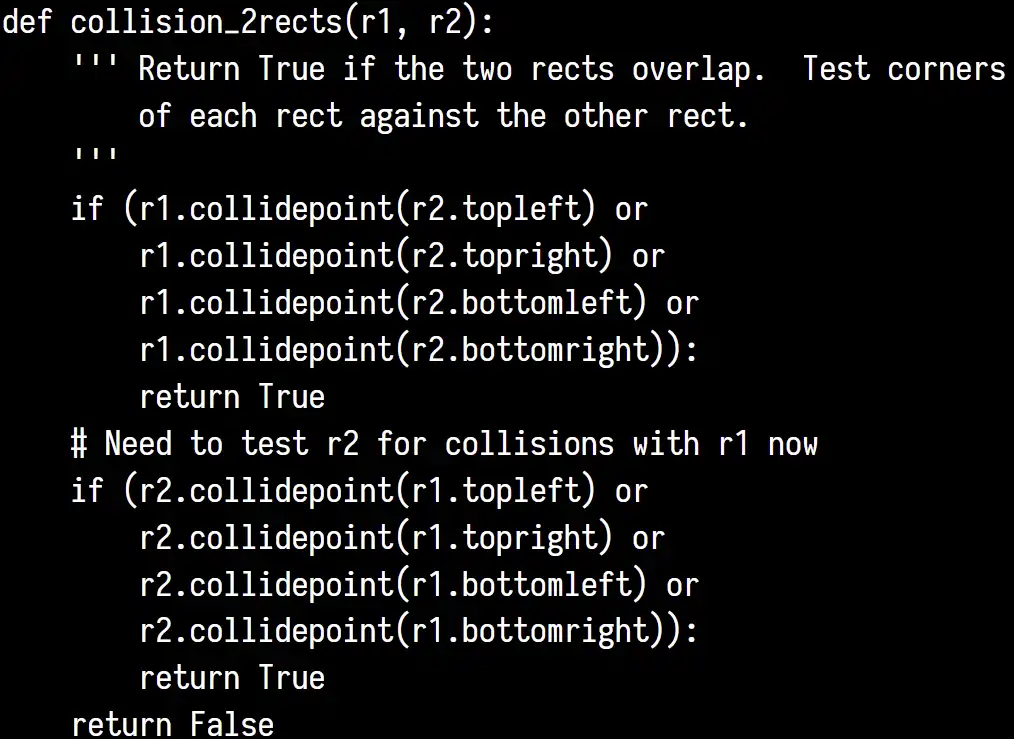
Warning

如果一个 rect 完全在另一个 rect 内部，可能会出现没有 collide 的判断 所以要双向判断

• {python}rect1.colliderect(rect2) 也可以

This is a bad approach

1. Tyranny of numbers: 需要比较太多次
2. Move-through: 一帧内位移太大就会穿过

Step 1. Reduce checks

• 没有移动的 obj，不需要和其他没有移动的 obj 进行检测
• 可以穿模的 obj (e.g. fire, grass) 不需要参与检测
• 将 obj 按照 group 组织，例如它们的相对位置不变时
• 距离较远的 obj 之间不需要进行检测，距离的阈值根据游戏需要来确定
• 屏幕之外的 obj 不一定需要进行检测，FPS
• 按照 area 进行划分，一些 obj 只会在一些 area 内部
• partitioning
  • 使用 quadtree 来组织 obj

Partitioning

Quadtree

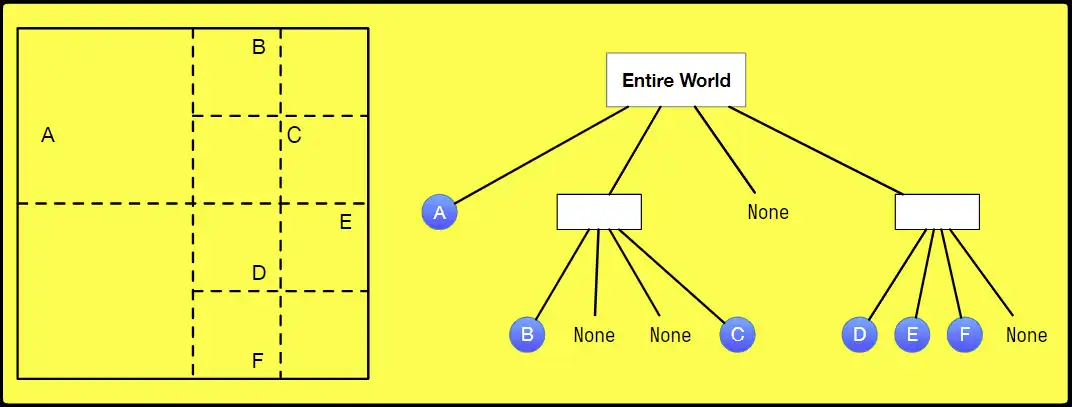
• might be managed based on classes of objs
  • e.g. a quad tree of all alien fighter ships
• 方便寻找最近邻
  • \(O(\log N)\) search

Tip

1. in 3-d? Octree!
2. BSP(Binary Space Partitioning) Tree
3. K-d tree 是另一种方法，是一种特殊的 BSPtree

Automated Partitioning

• Goldsmith-Salmon Inncremental Construction Method
• Bottom-up n-ary Clustering

Step 2. Quick tests

大部分没有被 reduce 的 check 其实都不会碰撞 rough test, 使用更加简单的形状来进行保守估计

Circle/Sphere test

(omitted)

Bounding Box test

• AABB
• OBB

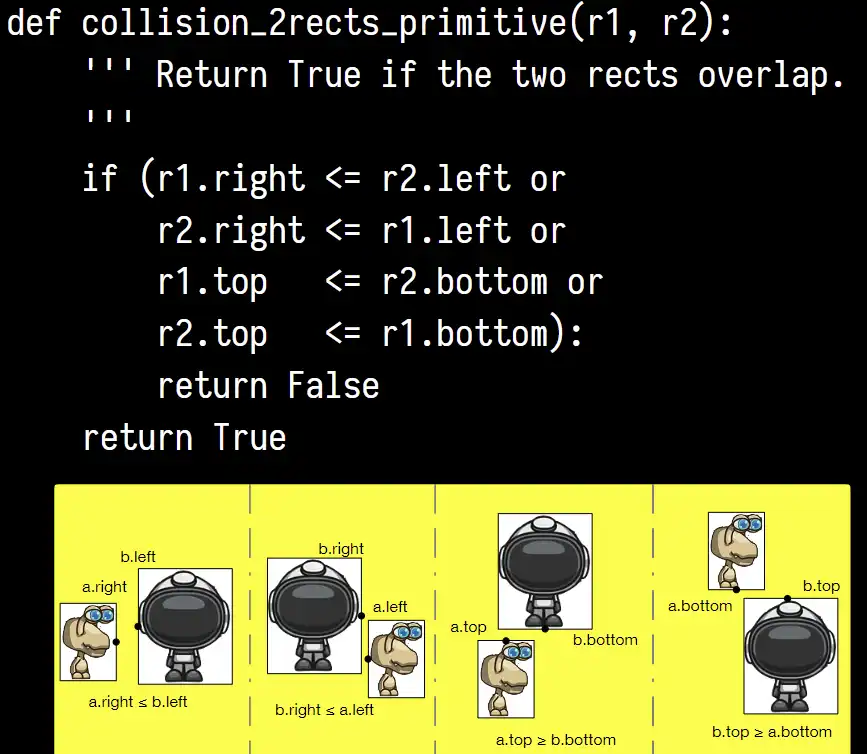
a better collide rect

先判断是否存在某个 axis 上的 overlap，如果有再进行进一步判断

Capsule test

• 主要是人物的近似
• 上下用 circle test，中间用 bounding box

Step 3. Precise tests

经过前两个步骤筛选后的 obj 需要进行精细的测试

Swept Sphere Algorithm

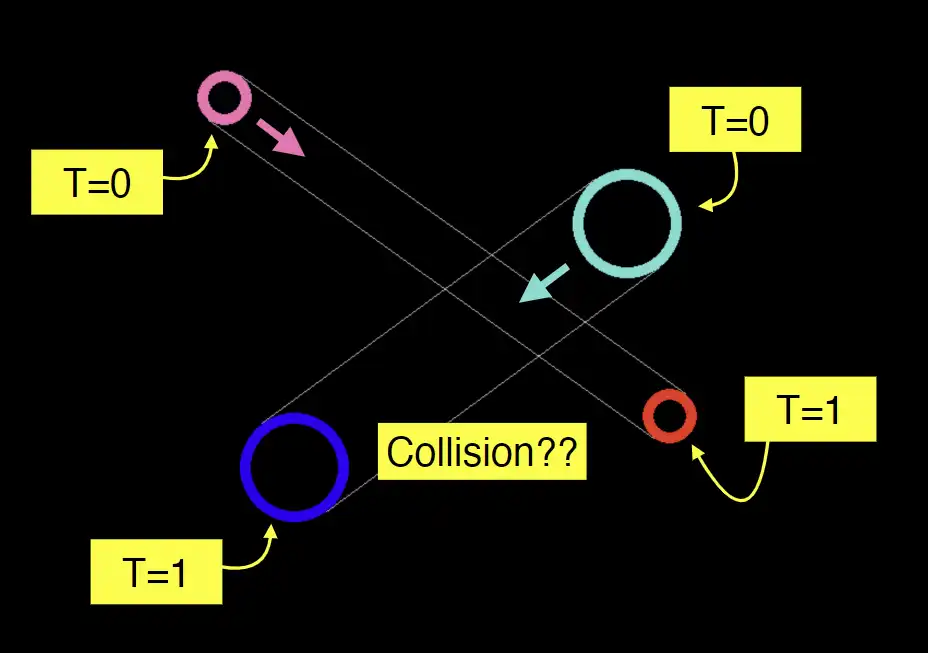
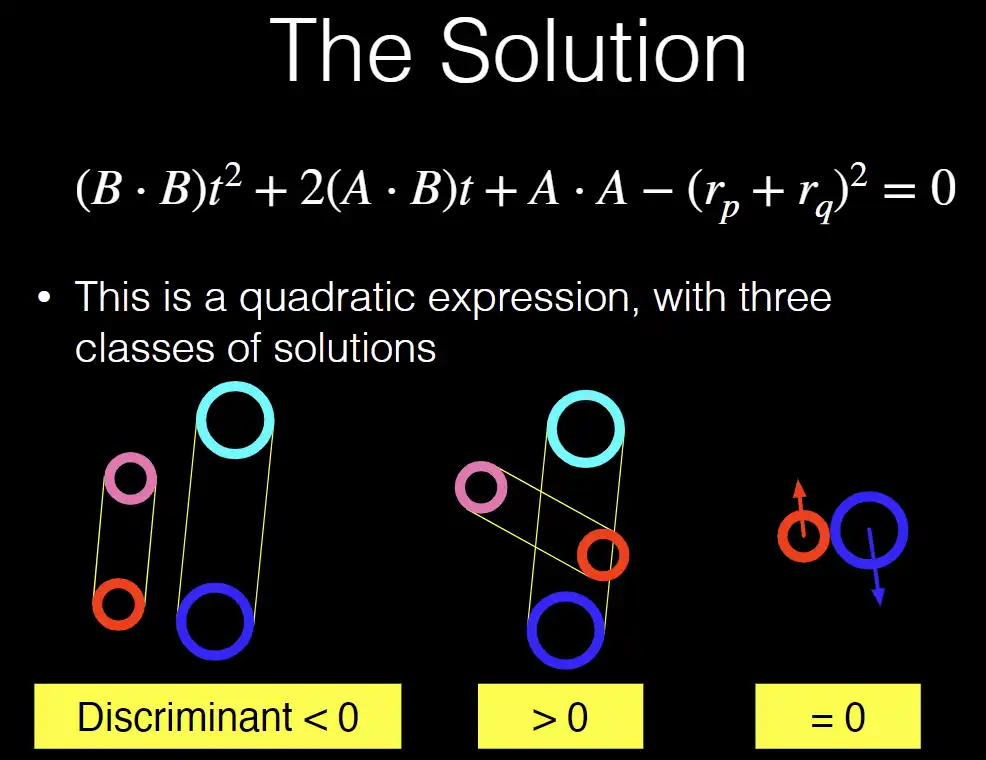
• 上面的方程代表，求解时间 \(t\)，使得中心距离为半径之和
• 所以根据判别式就能判断是否发生了碰撞
  • 如果 \(\Delta>0\)，需要求解 \(t\)
    • 如果 \(t \in(0,1)\)，会发生碰撞
    • 否则，不会发生碰撞
  • 否则，不会发生碰撞

Step 4. Resolve Collisions

• 子弹击中目标
• 撞墙、速度反向
• 弹性碰撞
  • 计算碰撞点
  • 碰撞切面
  • 速度大小
  • 结合 swept sphere 的结果

Comments